UVA1513 Movie collection

传送门

题意

KI先生有收集大量小电影的习惯, 他把他的珍藏理成一大摞。无论何时他想观看这一些电影的一部,他从这一摞电影中找出这一部电影,小心地将其拿出,以确保这一摞电影不会倒塌.

自从那一摞电影变得越来越大,他需要跟踪每一部电影的位置.或许了解每一部电影上面有多少部电影,就足以根据这些信息计算出其在这一摞电影中的位置.由一个印在电影盒子上的数字,可以识别出每一部电影.

那么你的任务就是编写一个跟踪每一部电影位置的程序,特别的,当KI先生从这一摞电影中拿出一部时,你的程序必须打印出在这一部即将被拿出的电影上面电影的数目.

输入

第一行是一个正整数t：输入数据的数量(t<=100),之后每一个测试数据,一行上是两个整数n,m, (1 ≤ n, m ≤ 100000),他们表示这一摞电影的数量和电影查询请求的数量.另一行是有m个整数, a1, . . . , am (1 ≤ ai ≤ n),他们表示KI先生想看的电影,它们需要你去查询定位.

为了简单起见,假设这一摞电影的编号1,2……n按顺序增加,其中这一摞电影最上面的是1号电影.

输出

每一组数据,输出一行整数, 其中第i个整数给出ai号电影在被拿出之前上方的电影的数目。请注意,在每次查询请求ai之后,ai号电影会被放在这一摞电影的顶部

Sample Input
2
3 3
3 1 1
5 3
4 4 5

Sample Output
2 1 0
3 0 4

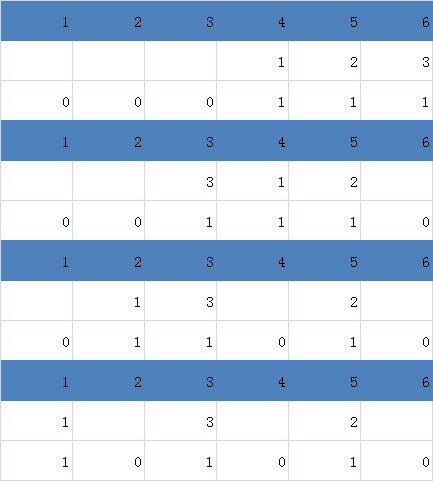
一道不错的思维题，这道题目的修改和查询操作比较简单，就是在拿出一张电影时，查询在它前面有多少元素，然后把它前面的数的位置都向后移动一位，但是我们如何实现将这张电影放到顶部呢？这不是删除和插入操作吗？然而我不会平衡树啊！！！于是这里有一种十分神奇的做法，可以巧妙的解决这个问题。由于要查询m次，也就是说我们要移动m次电影，所以我们可以开一个大小为（n+m）的树状数组，把每个数的权设为1，开始我们把n个数放在m+1---m+n的区间上，然后每进行一次查询a[i]作我们就将a[i]所在的位置-1，并把a[i]放到最前面，这样只需要不断地将元素前移就可以巧妙的解决问题了。

注意：uva对行末空格十分敏感，所以不能输出多余的空格。

 #include<iostream>
 #include<string>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<map>
 #include<algorithm>
 #include<stack>
 #include<queue>
 #include<vector>
 #define maxn 200005
 using namespace std;
 
 inline int read()
 {
     int x=,res=;
     char c=getchar();
     while(c<''||c>'')
     {
         if(c=='-')
         x=-;
         c=getchar();
     }
     while(c>=''&&c<='')
     {
         res=res*+(c-'');
         c=getchar();
     }
     return res*x;
 }
 
 int T,n,m,aa;
 int c[maxn<<],a[maxn];
 
 int low(int x)
 {
     return x&(-x);
 }
 
 void add(int x,int y)
 {
     for(int i=x;i<=n+m;i+=low(i))
     {
         c[i]+=y;
     }
 }
 
 int ask(int x)
 {
     int ans=;
     for(int i=x;i>;i-=low(i))
     {
         ans+=c[i];
     }
     return ans;
 }
 
 int main()
 {
     T=read();
     while(T--)
     {
         n=read();m=read();
         memset(c,,sizeof(c));
         int pd=;
         for(int i=m+;i<=m+n;i++)
         {
             a[i-m]=i;
             add(i,);
         }
         for(int i=;i<=m;i++)
         {
             aa=read();
             if(pd==)
             {
                 pd=;
             }
             else
             {
                 printf(" ");
             }
             printf("%d",ask(a[aa]-));
             add(a[aa],-);
             a[aa]=(m+-i);
             add(a[aa],);
         }
         printf("\n");
     }
     return ;
 }