Dijkstra求最短路径&例题

讲了半天好像也许maybe听懂了一点，先写下来233

先整理整理怎么存（开始绕）

最简单的是邻接矩阵存，但是开到10000*10000就MLE了,所以我们用链式前向星存（据说是叫这个名字吧）

这是个什么鬼玩意呢？

我们在记录时，以输入的顺序记录。

我们记录一条边，就记下它的终点(to)，权值（就是边长）(dis)，以及和这条边的起点相同，编号稍微小一点的边的编号(next)（开始绕）

这里我们记录当前每个点的所有出边（就是起点是这个点的边）中编号最大的那一条边（因为上面的next是编号稍微小的边）

当然也可以依据自己的习惯存储边

先上段代码

int head[nmax],n,m,s;//head[i] 是 以 点 i 为 起 点 ， 所 有 出 边 中 编 号 最 大 的 一 个
priority_queue<pair<int,int> > q;
void add(int fr,int _to,int _dis)
{    cnt++;
     eage[cnt].to=_to;
     eage[cnt].dis=_dis;
     eage[cnt].next=head[fr];//fr 为 from 的 简 写 , 这 里 的 以 点 i 为 起 点 的 边 多 了 一 条，
 //所 以 上 一 个 以 点 i 为 起 点 的 编 号 最 大 的 边 就 是 这 里 的 以 i 为 起 点 编 号 最 大 的 边 的 上 一 条 边
     head[fr]=cnt; //更 新 head[i]
}Edge [50001];
const int inf=;
int main()
{  scanf("%d%d%d",&n,&m,&o_node);
   dis[o_node]=;
   for(int i=;i<=m;i++)
   {int from,to,dis;
   cin>>from>>to>>dis;
     add(from,to,dis);
   }

这一坨是存图

拿张图举个例子

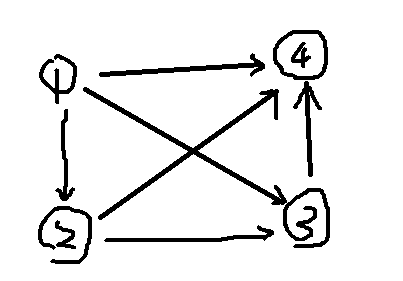
假设我们输入边的数据如下(三个数n,m,s,n为起点，m为终点，s为边长)

1 2 2

2 3 2

1 3 5

2 4 1

3 4 2

1 4 4

那代码中的存储如下

Edge[1].to=2,Edge[1].dis=2,Edge[1].next=0,head[1]=1(这里指没有上一条边),head[1]=1(这里head[i]记录的是以i为起点，当前最大编号出边的编号)

Edge[2].to=3,Edge[2].dis=2,Edge[2].next=0,head[2]=2

Edge[3].to=3,Edge[3].dis=5,Edge[3].next=1,head[1]=3

.....................................

讲完存图，再来说这个算法是怎么实现的

要求最短路径，这里有点类似贪心。

首先选择一个距离起点最近的直达点b，记录当前点与b的距离，再由b进行相同的扩展，来更新起点与其它点的距离

这样更新了一圈后就是最短距离，

再举个栗子

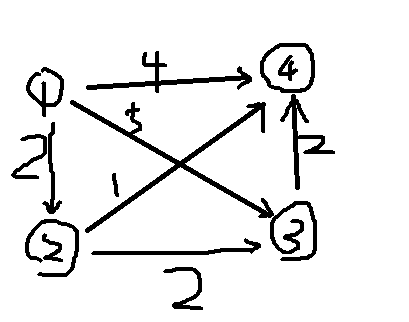
没错还是刚才那张图，这里标出了每条边的权值

按照dijkstra算法，我们首先找到距离①最近的直达点②，由②更新出①到④的最短路为3，①到③的最短路为4，

那么程序怎么实现呢？

看注释吧

（代码from gh,注释自己加的）

#include <iostream>
#include <cstdio>
#include <queue>

using namespace std;
const int INF = ;
struct edge
{
    int to, dis_, next;
} Edge[];
struct node
{
    int to, dis;
    inline friend bool operator<(const node &a, const node &b)
    {
        return a.dis < b.dis;//构造函数，将优先队列按照权值从小到大排序
    }
};
int head[], dis[];
bool vst[];
int nodenum, edgenum, origin_node, cnt = ;
priority_queue<node> q;//优先队列

inline void add_edge(int from, int to, int value)
{
    Edge[cnt].to = to;
    Edge[cnt].dis_ = value;
    Edge[cnt].next = head[from];
    head[from] = cnt++;
}

inline void dijkstra()
{
    for (register int i = ; i < origin_node; i++)
    {
        dis[i] = INF;//全部初始化为一个很大的数
    }
    dis[origin_node]=0;
    for (register int i = origin_node + ; i <= nodenum; i++)
    {
        dis[i] = INF;
    }
    q.push((node){origin_node, });
    while (!q.empty())//队不空（这里是当广搜来做的）
    {
        int x = q.top().to;
        q.pop();
        if (vst[x])//如果访问过，就跳过
            continue;
        vst[x] = ;
        for (register int i = head[x]; i; i = Edge[i].next)//从以x为起点的最后一条边开始，一直遍历完这个点的所有边
        {
            dis[Edge[i].to] = min(dis[Edge[i].to], dis[x] + Edge[i].dis_);//比较原来的大小和以x点为中转后的大小（取小的）
            q.push((node){Edge[i].to, -dis[Edge[i].to]});//入队
        }
    }
}

template <typename T_>
inline T_ getnum()
{
    T_ res = ;
    bool flag = false;
    char ch = getchar();
    while (!isdigit(ch))
    {
        flag = flag ? flag : ch == '-';
        ch = getchar();
    }
    while (isdigit(ch))
    {
        res = (res << ) + (res << ) + ch - '';
        ch = getchar();
    }
    return flag?-res:res;
}
template<typename T_>
inline void putnum(T_ num)
{
    if (num<)
    {
        putchar('-');
        num=-num;
    }
    if (num>)putnum(num/);
    putchar(''+num%);
}

int main()
{
    nodenum = getnum<int>(), dgenum  = getnum<int>(),origin_node = getnum<int>();
    for (register int i = ; i <= edgenum; i++)
    {
        register int f, t, v;
        f = getnum<int>(), t = getnum<int>(), v = getnum<int>();
        add_edge(f, t, v);
    }
    dijkstra();
    for (register int i=;i<=nodenum;putchar(' '),i++)
    {
        putnum<int>(dis[i]);
    }
    return ;
}

顺便附上一道dijkstra的题

一本通之城市路：

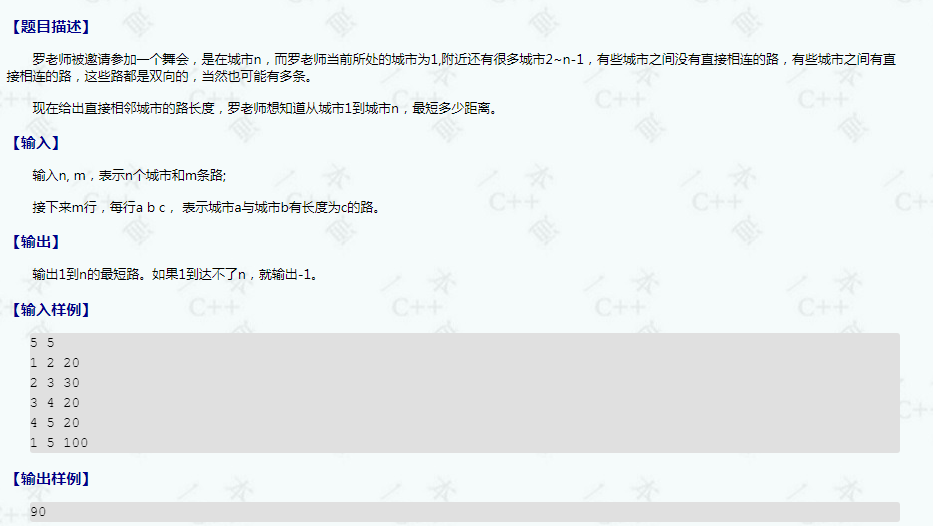
这个好像就是个模板哈

（代码from题解）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<set>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 3001
#define MOD 123
#define E 1e-6
using namespace std;
struct node{
    int pre;
    int next;
    int w;
}a[N*];
int n,m;
int cnt;
int head[N],vis[N],f[N];
void add(int x,int y,int w)
{
    cnt++;
    a[cnt].pre=y;
    a[cnt].next=head[x];
    a[cnt].w=w;
    head[x]=cnt;

    cnt++;
    a[cnt].pre=x;
    a[cnt].next=head[y];
    a[cnt].w=w;
    head[y]=cnt;
}//存图

int main()
{
    cin>>n>>m;
    for(int i=;i<=m;i++)
    {
        int x,y,w;
        cin>>x>>y>>w;
        add(x,y,w);
    }

    memset(f,INF,sizeof(f));
    f[]=;
    vis[]=;

    int x=head[];//手动模拟第一次出队
    while(x!=)
    {
        int y=a[x].pre;
        if(f[y]>a[x].w)
            f[y]=a[x].w;
        x=a[x].next;
    }

    int cnt=;
    while(cnt<n)//遍历所有的点
    {
        cnt++;
        int k;
        int minn=INF;
        for(int i=;i<=n;i++)
            if(vis[i]==&&f[i]<minn)
            {
                minn=f[i];
                k=i;
            }//先把能赋值的距离赋值上
        vis[k]=;

        int x=head[k];//手动模拟for循环
        while(x!=)//这里木有队列，所以要while循环一次处理完
        {
            int y=a[x].pre;
            int w=a[x].w;
            if(vis[y]==&&f[y]>f[k]+w)
                f[y]=f[k]+w;
            x=a[x].next;
        }
    }

    if(f[n]==INF)
        cout<<"-1"<<endl;
    else
        cout<<f[n]<<endl;
    return ;
}

 堆优化

我们上面说到dij是先挑距离起点最近的一个点b搞，然后再找距离b最近的点搞，那么每次判断距离就有点麻烦。我们换成每次挑距离起点最近的点搞，这样我们可以用堆（priority_queue）来维护距离起点最近的那个点，时间复杂度O(nmlogn)

代码：

#include<bits/stdc++.h>
#define pa pair<int,int>
using namespace std;
inline int read()
{
    char ch=getchar();
    int x=;bool f=;
    while(ch<''||ch>'')
    {
        if(ch=='-')f=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return f?-x:x;
}
int n,m,dis[],cnt,head[],s;
struct Ed{
    int to,dis,nxt;
}edge[];
inline void add(int fr,int to,int dis)
{
    cnt++;
    edge[cnt].to=to;
    edge[cnt].dis=dis;
    edge[cnt].nxt=head[fr];
    head[fr]=cnt;
}
priority_queue<pa,vector<pa>,greater<pa> > q;//大根堆转小根堆
bool vis[];
inline void dij(int s)
{
    for(int i=;i<=n;i++)
     dis[i]=;
    dis[s]=;
    q.push(make_pair(,s));
    while(!q.empty())
    {
        int now=q.top().second;
        q.pop();
        if(vis[now])continue;
        vis[now]=;
        for(int e=head[now];e;e=edge[e].nxt)
        {
            int v=edge[e].to;
            if(dis[now]+edge[e].dis<dis[v])
            {
                dis[v]=dis[now]+edge[e].dis;
                q.push(make_pair(dis[v],v));
            }
        }
    }
}
int main()
{
    n=read();m=read();s=read();
    for(int i=;i<=m;i++)
    {
        int u=read(),v=read(),w=read();
        add(u,v,w);
    }
    dij(s);
    for(int i=;i<=n;i++)
     printf("%d ",dis[i]);
}