「CTSC2018」暴力写挂

毫无$ Debug$能力

全世界就我会被卡空间.jpg

LOJ #2553

UOJ #400

Luogu P4565

---

题意

给定两棵树$ T,T'$，求一组点对$ (x,y)$使得$deep(x)+deep(y)-deep(LCA(x,y))-deep'(LCA'(x,y))$尽量大

$ x$可以等于$ y$，点数不超过$ 366666$，边有边权

---

$ Solution$

枚举$T'$的一个点$ u$作为$LCA'(x,y)$，则$ x,y$必然在$u$的不同子树或者就是点$u$

则

$ ans=max(ans,deep[x]+deep[y]-deep[LCA(x,y)]-deep[u])$

直接做复杂度过大

考虑$ deep[x]+deep[y]-deep[LCA(x,y)]=\frac{1}{2}(deep[x]+deep[y]+dist(x,y))$

这样有根树就转化成了无根树

考虑对$ T$边分,将$ T$转化成可边分二叉树之后建出边分树（可能不用完全建出来？）然后记录每个叶子节点的路径

比如树

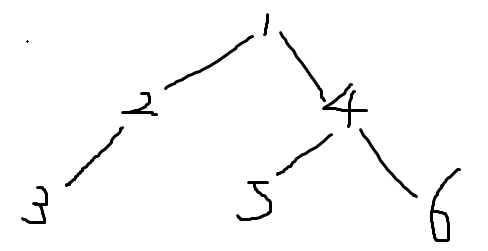
的其中一棵边分树为

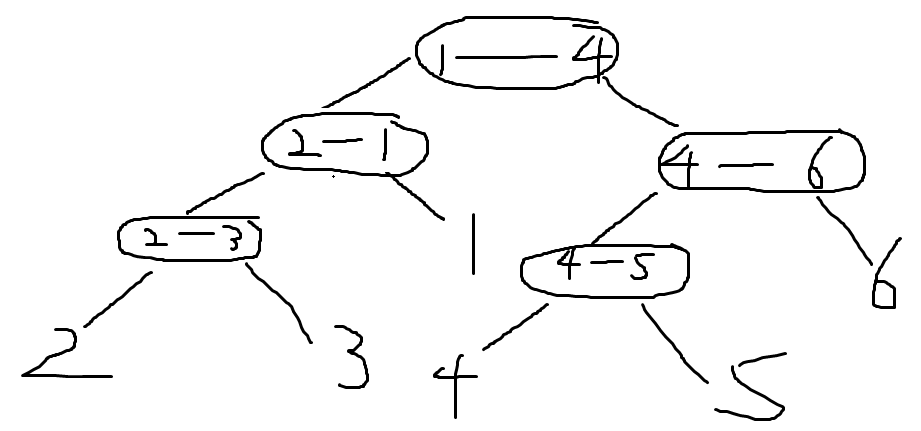
用一个$ 01$串记录到每个叶子节点的路径

边分树有两个优美的性质

1.边分树的深度是$ log(n)$级别的

2.边分树每棵子树中的叶子节点在原树上一定连通

如果一条路径经过了边分树上某条边节点

则这条路径一定为（边节点左边子树的某个点节点到边节点的左端点）+（边节点右边子树的某个点节点到边节点的右端点）+边长度

而每对点$ (x,y)$的贡献的两倍为$ deep[x]+deep[y]+dist(x,y)$

因此我们可以在每个节点记录（其子树内点节点到它的路径长度+该点深度）的最大值$ Max$

然后在每个边节点处处理贡献

一开始边分树中所有点节点尚未被"激活"因此所有节点的$ Max$值都是$ -INF$

如果一个点节点可被使用则将其激活，将这个点在边分树的位置到边分树的根的这段路经的所有$ Max$进行更新

并与途中统计答案

枚举$ T'$的每个节点

新建一棵空的边分树（即所有点节点都尚未被激活）

将其于$ T'$内的所有子节点"激活"并在过程中统计答案是一种可行做法

复杂度过大无法接受

容易发现边分树很像线段树可以动态开点插入

加上可以像线段树合并一样，这个点的边分树可以依次合并其所有子节点的边分树

并在过程中统计答案

复杂度大概是$ O(n log n)$的

（好像还是讲不太清楚啊...）

---

$ my \ code$

#include<ctime>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
#define M 850010
#define rt register int
#define ll long long
using namespace std;
namespace fast_IO{
    const int IN_LEN=,OUT_LEN=;
    char ibuf[IN_LEN],obuf[OUT_LEN],*ih=ibuf+IN_LEN,*oh=obuf,*lastin=ibuf+IN_LEN,*lastout=obuf+OUT_LEN-;
    inline char getchar_(){return (ih==lastin)&&(lastin=(ih=ibuf)+fread(ibuf,,IN_LEN,stdin),ih==lastin)?EOF:*ih++;}
}
using namespace fast_IO;
#define getchar() getchar_()
inline ll read(){
    ll x=;char zf=;char ch=getchar();
    while(ch!='-'&&!isdigit(ch))ch=getchar();
    if(ch=='-')zf=-,ch=getchar();
    while(isdigit(ch))x=x*+ch-'',ch=getchar();return x*zf;
}
void write(ll y){if(y<)putchar('-'),y=-y;if(y>)write(y/);putchar(y%+);}
void writeln(const ll y){write(y);putchar('\n');}
int k,m,n,x,y,z,cnt,ans,la,p[M],lg2[M*],up[][M*],q[M*],tt,dt[M];
ll deep0[M],deep2[M/];
struct node{int a,c;};
vector<node>e[M];
struct Tree{
    int F[M],L[M],N[M*],a[M*],c[M*],k=;
    void dfs(int x,int pre,int id){
        q[++tt]=x;p[x]=tt;
        for(rt i=F[x];i;i=N[i])if(a[i]!=pre){
            if(id==)deep0[a[i]]=deep0[x]+c[i];
            else deep2[a[i]]=deep2[x]+c[i];
            dt[a[i]]=dt[x]+;
            dfs(a[i],x,id);
            q[++tt]=x;
        }
    }
    void add(int x,int y,int z){
        a[++k]=y;c[k]=z;
        if(!F[x])F[x]=k;
        else N[L[x]]=k;
        L[x]=k;
    }
    void init(int x,int pre){
        for(rt i=F[x];i;i=N[i])if(a[i]!=pre){
            e[x].push_back({a[i],c[i]});
            init(a[i],x);
        }
    }
    int LCA(int x,int y){
        int L=p[x],R=p[y];if(L>R)swap(L,R);int len=lg2[R-L+];
        if(dt[up[len][L]]<dt[up[len][R-(<<len)+]])
        return up[len][L];else return up[len][R-(<<len)+];
    }
    void LCA_init(){
        for(rt i=;i<=tt;i++)up[][i]=q[i];
        for(rt i=;i<=;i++)
        for(rt j=;j<=tt;j++)
        if(dt[up[i-][j]]<dt[up[i-][j+(<<i-)]])up[i][j]=up[i-][j];
        else up[i][j]=up[i-][j+(<<i-)];
        for(rt i=;i<=tt;i++)lg2[i]=lg2[i>>]+;
    }
    ll dis(int x,int y){return deep0[x]+deep0[y]-2ll*deep0[LCA(x,y)];}
}T0,T1,T2;

void rebuild(){
    for(rt i=;i<=n;i++){
        if(e[i].size()<=){
            for(auto j:e[i])T0.add(i,j.a,j.c*(j.a<=la)),T0.add(j.a,i,j.c*(j.a<=la));
            continue;
        }
        int i0=++n,i1=++n;deep0[i0]=deep0[i1]=deep0[i];
        for(rt j=;j<e[i].size();j++)if(j&)
        e[i0].push_back({e[i][j].a,e[i][j].c});else e[i1].push_back({e[i][j].a,e[i][j].c});
        T0.add(i,i0,);T0.add(i0,i,);T0.add(i,i1,);T0.add(i1,i,);
        e[i].shrink_to_fit();
    }
}
int id,nowmin,all,size[M];
bool vis[M];
void get(int x,int pre){
    size[x]=;
    for(rt i=T0.F[x];i;i=T0.N[i])if(!vis[i>>]&&T0.a[i]!=pre){
        get(T0.a[i],x);size[x]+=size[T0.a[i]];
        const int now=abs(all-size[T0.a[i]]-size[T0.a[i]]);
        if(now<nowmin)nowmin=now,id=i;
    }
}
string path[M];
int ww=;
int ls[M],rs[M],L[M],R[M],top,len[M];
void solve(int x,int sz,int&it,string s){
    if(sz==)return path[x]=s,void();
    nowmin=all=sz;if(!it)it=++ww;
    get(x,x);vis[id>>]=;

    int xx=T0.a[id],yy=T0.a[id^],siz=size[xx];
    L[it]=xx;R[it]=yy;len[it]=T0.c[id];
    solve(xx,siz,ls[it],s+'');solve(yy,sz-siz,rs[it],s+'');
}
struct tree{
    int ls,rs;ll Max;
}t[M*];
int bb=;
void insert(ll &ret,int &x,int y,int pl,int id){//在第x棵树插入第y个点
    if(!x)x=++bb,t[x].Max=-100000000000000ll;
    int sz=path[y].size();
    if(pl==sz)return;

    if(path[y][pl]==''){
        insert(ret,t[x].ls,y,pl+,ls[id]);
        t[t[x].ls].Max=max(t[t[x].ls].Max,deep0[y]+T0.dis(y,L[id]));
    }
    else{
        insert(ret,t[x].rs,y,pl+,rs[id]);
        t[t[x].rs].Max=max(t[t[x].rs].Max,deep0[y]+T0.dis(y,R[id]));
    }
    ret=max(ret,t[t[x].ls].Max+t[t[x].rs].Max+len[id]);
}
int root[M];
int merge(ll &ret,int x,int y,int id){
    if(!x)return y;if(!y)return x;
    t[x].Max=max(t[x].Max,t[y].Max);
    ret=max(ret,t[t[x].ls].Max+t[t[y].rs].Max+len[id]);
    ret=max(ret,t[t[y].ls].Max+t[t[x].rs].Max+len[id]);

    t[x].ls=merge(ret,t[x].ls,t[y].ls,ls[id]);
    t[x].rs=merge(ret,t[x].rs,t[y].rs,rs[id]);

    return x;
}
ll ret=-100000000000000ll;
void calc(int x,int pre){
    ll ans=-100000000000000ll;
    insert(ans,root[x],x,,);
    for(rt i=T2.F[x];i;i=T2.N[i])if(T2.a[i]!=pre){
        calc(T2.a[i],x);
        root[x]=merge(ans,root[x],root[T2.a[i]],);
        ret=max(ret,ans-2ll*deep2[x]);
    }
}
int main(){
    la=n=read();t[].Max=-100000000000000ll;
    for(rt i=;i<n;i++){
        x=read();y=read();z=read();
        T1.add(x,y,z);
        T1.add(y,x,z);
    }
    for(rt i=;i<n;i++){
        x=read();y=read();z=read();
        T2.add(x,y,z);
        T2.add(y,x,z);
    }
    T2.dfs(,,);T1.init(,);rebuild();
    tt=;T0.dfs(,,),T0.LCA_init();
    int pl=;
    solve(,n,pl,"");
    calc(,);ret/=;
    for(rt i=;i<=la;i++)ret=max(ret,deep0[i]-deep2[i]);
    cout<<ret;
    return ;
}