深度学习(九) 深度学习最全优化方法总结比较(SGD,Momentum,Nesterov Momentum,Adagrad,Adadelta,RMSprop,Adam)
前言
这里讨论的优化问题指的是,给定目标函数f(x),我们需要找到一组参数x(权重),使得f(x)的值最小。
本文以下内容假设读者已经了解机器学习基本知识,和梯度下降的原理。
SGD
SGD指stochastic gradient descent,即随机梯度下降。是梯度下降的batch版本。
对于训练数据集,我们首先将其分成n个batch,每个batch包含m个样本。我们每次更新都利用一个batch的数据,而非整个训练集。即:
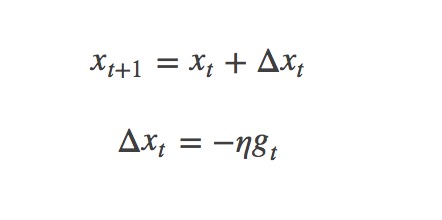
其中,η为学习率,gt为x在t时刻的梯度。
这么做的好处在于:
- 当训练数据太多时,利用整个数据集更新往往时间上不显示。batch的方法可以减少机器的压力,并且可以更快地收敛。
- 当训练集有很多冗余时(类似的样本出现多次),batch方法收敛更快。以一个极端情况为例,若训练集前一半和后一半梯度相同。那么如果前一半作为一个batch,后一半作为另一个batch,那么在一次遍历训练集时,batch的方法向最优解前进两个step,而整体的方法只前进一个step。
Momentum
SGD方法的一个缺点是,其更新方向完全依赖于当前的batch,因而其更新十分不稳定。解决这一问题的一个简单的做法便是引入momentum。
momentum即动量,它模拟的是物体运动时的惯性,即更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度微调最终的更新方向。这样一来,可以在一定程度上增加稳定性,从而学习地更快,并且还有一定摆脱局部最优的能力:

其中,ρ 即momentum,表示要在多大程度上保留原来的更新方向,这个值在0-1之间,在训练开始时,由于梯度可能会很大,所以初始值一般选为0.5;当梯度不那么大时,改为0.9。η 是学习率,即当前batch的梯度多大程度上影响最终更新方向,跟普通的SGD含义相同。ρ 与 η 之和不一定为1。
Nesterov Momentum
这是对传统momentum方法的一项改进,由Ilya Sutskever(2012 unpublished)在Nesterov工作的启发下提出的。
首先,按照原来的更新方向更新一步(棕色线),然后在该位置计算梯度值(红色线),然后用这个梯度值修正最终的更新方向(绿色线)。上图中描述了两步的更新示意图,其中蓝色线是标准momentum更新路径。
公式描述为:
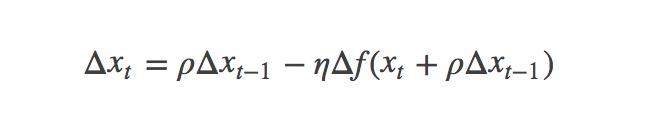
Adagrad
Adagrad其实是对学习率进行了一个约束。即:
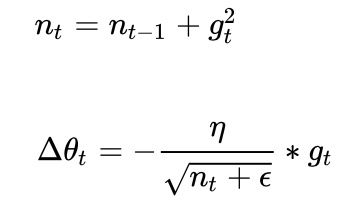
此处,对从1到
进行一个递推形成一个约束项regularizer,
,
用来保证分母非0
特点:
- 前期
较小的时候, regularizer较大,能够放大梯度
- 后期
较大的时候,regularizer较小,能够约束梯度
- 适合处理稀疏梯度
缺点:
- 由公式可以看出,仍依赖于人工设置一个全局学习率
设置过大的话,会使regularizer过于敏感,对梯度的调节太大
- 中后期,分母上梯度平方的累加将会越来越大,使
,使得训练提前结束
Adadelta
Adadelta是对Adagrad的扩展,最初方案依然是对学习率进行自适应约束,但是进行了计算上的简化。Adagrad会累加之前所有的梯度平方,而Adadelta只累加固定大小的项,并且也不直接存储这些项,仅仅是近似计算对应的平均值。即:
在此处Adadelta其实还是依赖于全局学习率的,但是作者做了一定处理,经过近似牛顿迭代法(求根点)之后:
其中,代表求期望。
此时,可以看出Adadelta已经不用依赖于全局学习率了。
特点:
- 训练初中期,加速效果不错,很快
- 训练后期,反复在局部最小值附近抖动
RMSprop
RMSprop可以算作Adadelta的一个特例:
当时,
就变为了求梯度平方和的平均数。
如果再求根的话,就变成了RMS(均方根):
此时,这个RMS就可以作为学习率的一个约束:
特点:
- 其实RMSprop依然依赖于全局学习率
- RMSprop算是Adagrad的一种发展,和Adadelta的变体,效果趋于二者之间
- 适合处理非平稳目标- 对于RNN效果很好
Adam
Adam(Adaptive Moment Estimation)本质上是带有动量项的RMSprop,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。公式如下:
其中,,
分别是对梯度的一阶矩估计和二阶矩估计,u和v为衰减率,u通常为0.9,v通常为0.999,可以看作对期望
,
的估计;
,
是对
,
的校正,这样可以近似为对期望的无偏估计。可以看出,直接对梯度的矩估计对内存没有额外的要求,而且可以根据梯度进行动态调整,而
对学习率形成一个动态约束,而且有明确的范围。
特点:
- 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
- 对内存需求较小
- 为不同的参数计算不同的自适应学习率
- 也适用于大多非凸优化- 适用于大数据集和高维空间
深度学习(九) 深度学习最全优化方法总结比较(SGD,Momentum,Nesterov Momentum,Adagrad,Adadelta,RMSprop,Adam)的更多相关文章
- [深度学习] 最全优化方法总结比较--SGD,Adagrad,Adadelta,Adam,Adamax,Nadam
SGD 此处的SGD指mini-batch gradient descent,关于batch gradient descent, stochastic gradient descent, 以及 min ...
- 深度学习最全优化方法总结比较(SGD,Adagrad,Adadelta,Adam,Adamax,Nadam)(转)
转自: https://zhuanlan.zhihu.com/p/22252270 ycszen 另可参考: https://blog.csdn.net/llx1990rl/article/de ...
- 深度学习最全优化方法总结比较及在tensorflow实现
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明. 本文链接:https://blog.csdn.net/u010899985/article/d ...
- 深度学习——优化器算法Optimizer详解(BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam)
在机器学习.深度学习中使用的优化算法除了常见的梯度下降,还有 Adadelta,Adagrad,RMSProp 等几种优化器,都是什么呢,又该怎么选择呢? 在 Sebastian Ruder 的这篇论 ...
- 学习笔记DL002:AI、机器学习、表示学习、深度学习,第一次大衰退
AI早期成就,相对朴素形式化环境,不要求世界知识.如IBM深蓝(Deep Blue)国际象棋系统,1997,击败世界冠军Garry Kasparov(Hsu,2002).国际象棋,简单领域,64个位置 ...
- (转载)深度剖析 | 可微分学习的自适配归一化 (Switchable Normalization)
深度剖析 | 可微分学习的自适配归一化 (Switchable Normalization) 作者:罗平.任家敏.彭章琳 编写:吴凌云.张瑞茂.邵文琪.王新江 转自:知乎.原论文参考arXiv:180 ...
- 深度学习笔记:优化方法总结(BGD,SGD,Momentum,AdaGrad,RMSProp,Adam)
深度学习笔记:优化方法总结(BGD,SGD,Momentum,AdaGrad,RMSProp,Adam) 深度学习笔记(一):logistic分类 深度学习笔记(二):简单神经网络,后向传播算法及实现 ...
- 【深度学习】Pytorch 学习笔记
目录 Pytorch Leture 05: Linear Rregression in the Pytorch Way Logistic Regression 逻辑回归 - 二分类 Lecture07 ...
- 截图:【炼数成金】深度学习框架Tensorflow学习与应用
创建图.启动图 Shift+Tab Tab 变量介绍: F etch Feed 简单的模型构造 :线性回归 MNIST数据集 Softmax函数 非线性回归神经网络 MINIST数据集分类器简单版 ...
随机推荐
- 英语知识积累-D01-body+animal
My body What's your name? Here are lots of children playing. Are they happy or sad? Who's waving at ...
- 在VB中动态执行VBS代码,可操控窗体控件
通过执行一段VBS代码来操控窗体内的控件也可以使用AddObject方法添加自己的类,那么在动态VBS代码中也一样可以使用在增加程序扩展性或是有脚本化需求的时候,这个方法还是不错的. Option E ...
- Caused by: org.apache.ibatis.builder.BuilderException: Parsing error was found in mapping #{}. Check syntax #{property|(expression), var1=value1, var2=value2, ...}
解决办法:查看与该项目中的所有#{},应该是 #{}的中间没有写值
- IIS 设置
解决办法:1. 1).通过webconfig中增加模拟,加入管理员权限, <identity impersonate="true" userName="系统管理员& ...
- vue的风格指南(必要的)
1.v-if与v-for不要放在同一个元素上 当 v-if 与 v-for 一起使用时,v-for 具有比 v-if 更高的优先级.永远不要把 v-if 和 v-for 同时用在同一个元素上. 一般我 ...
- 你不知道的JS之 this 和对象原型(一)this 是什么
原文:你不知道的js系列 JavaScript 的 this 机制并没有那么复杂 为什么会有 this? 在如何使用 this 之前,我们要搞清楚一个问题,为什么要使用 this. 下面的代码尝试去 ...
- java发送短信验证码
业务: 手机端点击发送验证码,请求发送到java服务器端,由java调用第三方平台(我们使用的是榛子云短信http://smsow.zhenzikj.com)的短信接口,生成验证码并发送. SDK下载 ...
- topic的leader显示为none的解决办法
1.查看kafka的topic详细信息 bin/kafka-topics.sh --zookeeper 127.0.0.1:2181 --topic test --describe 配置delete. ...
- qt5.4解决输出中文乱码问题
需要在字符串前添加 QString::fromUtf8 例: b2 = new QPushButton(this); b2->setText(QString::fromUtf8("变化 ...
- Anveshak: Placing Edge Servers In The Wild
Anveshak:在野外放置边缘服务器 本文为SIGCOMM 2018 Workshop (Mobile Edge Communications, MECOMM)论文. 笔者翻译了该论文.由于时间仓促 ...

