[模板] 后缀自动机&&后缀树

后缀自动机

后缀自动机是一种确定性有限状态自动机, 它可以接收字符串$s$的所有后缀.

构造, 性质

翻译自毛子俄罗斯神仙的博客, 讲的很好

后缀自动机详解 - DZYO的博客 - CSDN博客

下面是一些note:

定义

对于字符串$s$的子串$t$, $endpos(t)$ (或者 $right(t)$ ) 表示t在s中出现位置的右端点的集合.
- $endpos$互不相交.
- 有相同 $endpos$ 集合的字符串构成一个等价类.
- 对于每个等价类, 包含的字符串长度为$[len(p), maxlen(p)]$ , 是一个连续的区间.
后缀自动机的节点 $p$ 代表一个 $endpos$ 相同的子串的集合.
对于后缀自动机的节点 $p$, $parent(p)$ (或者 $link(p)$ ) 表示p在不同等价类中的最长后缀.
- $parent$ 形成一棵树关系.
- $len(p) = maxlen(parent(p)) +1$

构建 && 状态数/转移数线性证明

上面的blog已经写的很好了, 我就不重写一遍了:P

示意图

字符串 ab:

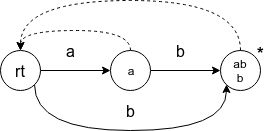
其中 * 代表终止节点, 虚箭头表示 $fa(p)$.

字符串 abb:

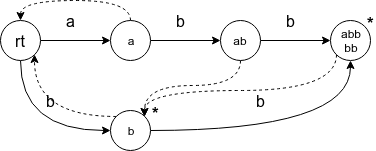
字符串 bba 的后缀树 (见后), 即字符串 abb 的前缀树/后缀自动机的 parent 树:

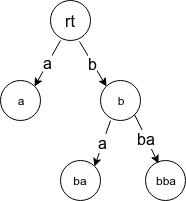
Code

const int nsz=1e6+50,ndsz=2*nsz,csz=27;

ll n;

char s[nsz];

//sam

//p.l means maxlen(p)

struct tnd{int ch[csz],l,fa,cnt;}sam[ndsz];

#define ch(p,c) sam[p].ch[c]

#define fa(p) sam[p].fa

int ps=1,las=1;

int cnt[ndsz],c[ndsz],seq[ndsz];

void insert(int c){

	int p=las;

	las=++ps,sam[las].l=sam[p].l+1,cnt[las]=1;

	for(;p&&ch(p,c)==0;p=fa(p))ch(p,c)=las;

	if(p==0)fa(las)=1;

	else{

		int q=ch(p,c);

		if(sam[q].l==sam[p].l+1)fa(las)=q;

		else{

			int q1=++ps;

			sam[q1]=sam[q],sam[q1].l=sam[p].l+1,fa(q)=fa(las)=q1;

			for(;p&&ch(p,c)==q;p=fa(p))ch(p,c)=q1;

		}

	}

}

void build(){

	rep(i,1,n)insert(s[i]-'a');

}

struct te{int t,pr;}edge[ndsz];

int hd[ndsz],pe=1;

void adde(int f,int t){edge[++pe]=(te){t,hd[f]};hd[f]=pe;}

void buildtr(){

	rep(i,2,ps)adde(fa(i),i);

}

void gettp(){ //topo sort

	rep(i,1,ps)++c[sam[i].l];

	rep(i,1,ps)c[i]+=c[i-1];

	rep(i,1,ps)seq[c[sam[i].l]--]=i;

}

void match(char *s,int n){

	int cur=1,l=0;

	rep(i,1,n){

		if(ch(cur,s[i])){++l,cur=ch(cur,s[i]);}

		else{

			while(cur&&ch(cur,s[i])==0)cur=fa(cur);

			if(cur==0)l=0,cur=1;

			else l=sam[cur].l+1,cur=ch(cur,s[i]);

		}

	}

}

后缀树

后缀树是对字符串 $S$ 的所有后缀建立的trie树, 同样可以识别 $S$ 的所有后缀.

为了节省空间, 可以利用虚树的思想. 我们把只有一个子节点的节点压缩到它的父亲, 也就是说, 把没有分叉的一条链压缩成一条边.

显然, 这样建成的后缀 trie 只会保留每个后缀的终止节点('\0'), 和他们的lca. 这两者数量都是 $O(n)$ 的, 因此状态总数也为 $O(n)$ .

同时, 字符串 $S$ 后缀自动机的parent树等价于 $S$ 逆序 $S'$ 的后缀树, 可以称作前缀树. 证明见[3].

几个关键问题

在后缀自动机上走路的时间复杂度

23333

就是说对字符串 $S$ 建立后缀自动机, 然后将字符串 $T$ 从起点走转移边, 如果没有转移边则跳parent指针. 这样可以求出 $S$ 与 $T$ 的每一个公共子串.

记当前 $S$ 与 $T$ 的匹配长度为 $l$. 对于每一次转移, $l$ 会加 $1$; 对于跳parent指针, $l$ 会减少, 而 $l$ 总的减少不会超过 $|T|$. 因此总时间复杂度为 $O(|T|)$.

事实上, 对于insert(c)的均摊时间复杂度的分析是类似的.

代码

//l : max len of current matched string

//p : current state

void match(char *s,int n){

	int cur=1,l=0;

	rep(i,1,n){

		if(ch(cur,s[i])){++l,cur=ch(cur,s[i]);}

		else{

			while(cur&&ch(cur,s[i])==0)cur=fa(cur);

			if(cur==0)l=0,cur=1;

			else l=sam[cur].l+1,cur=ch(cur,s[i]);

		}

	}

}

拓扑序

from [2]

SAM 中的 DAWG 满足一个性质，如果有一条转移边 $u \rightarrow v$ ，则一定有 $|\max(u)| < |\max(v)|$。类似的，如果 $\text{next}(v) = u$，也有 $|\max(u)| < |\max(v)|$。所以，按照每个节点记录的 max 长度排序，可以同时得到 DAWG 和前缀树的拓扑序。

使用桶排序, 那么时间复杂度是$O(n)$.

代码

void gettp(){ //topo sort

	rep(i,1,ps)++c[sam[i].l];

	rep(i,1,ps)c[i]+=c[i-1];

	rep(i,1,ps)seq[c[sam[i].l]--]=i;

}

这样我们就可以在SAM上进行动态规划.

每个节点代表字符串个数

由定义可知,

节点 $p$ 代表字符串个数 $ = maxlen(p)-len(p)+1 = maxlen(p)-maxlen(parent(p))$.

同时, 节点 $p$ 代表字符串个数 = 起点到节点 $p$ 路径数.

求endpos集合

记非拷贝而来的节点为实节点, 否则为虚节点.

当实节点为第 $t$ 个字符加入时建立的时, 它的endpos集合中显然有 $t$, 并且它是endpos集合中有 $t$ 的节点中maxlen最大的.

那么它的parent节点显然也包含$t$, 直接跳parent()即可.

这时我们可以O(n)的求出endpos集合的大小:

对于不是拷贝的节点, cnt设为1; 拷贝而来的节点, cnt设为0.
在parent树上dp, $cnt_p+=\sum_{parent(v)=p} cnt_v$.
$cnt_p$ 表示这个节点endpos集合大小, 也就是在字符串中的出现次数.

如果要求endpos集合, 需要可合并数据结构 (线段树/set/堆等). 利用可持久化线段树合并 ([模板] 线段树合并) 可以求出所有点的 endpos 集合.

最小表示法

建立$S+S$的后缀自动机, 从起点开始, 每次走字典序最小的转移, 并记录.

转移 $|S|$ 次之后, 得到的字符串即为 $S$ 的最小表示.

后缀自动机的用法

拓扑序 dp (自动机上/parent树上)
利用 len 函数和 endpos 集合 (dp, 线段树合并等)
利用 parent 树
- 树上的技巧: lca, 倍增, 点分治, 树剖, LCT
- dp(自上向下, 自下向上, 双重, 倍增)
利用自动机的性质 (转移等)

参考资料