[Reinforcement Learning] 马尔可夫决策过程

在介绍马尔可夫决策过程之前，我们先介绍下情节性任务和连续性任务以及马尔可夫性。

情节性任务 vs. 连续任务

• 情节性任务（Episodic Tasks），所有的任务可以被可以分解成一系列情节，可以看作为有限步骤的任务。
• 连续任务（Continuing Tasks），所有的任务不能分解，可以看作为无限步骤任务。

马尔可夫性

引用维基百科对马尔可夫性的定义：

马尔可夫性：当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。

用数学形式表示如下：

A state \(S_t\) is Markov if and only if
\[P[S_{t+1}|S_t] = P[S_{t+1}|S_1, ..., S_t]\]

马尔可夫过程

马尔可夫过程即为具有马尔可夫性的过程，即过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态都是独立、不相关的。

马尔可夫奖赏过程

马尔可夫奖赏过程（Markov Reward Process，MRP）是带有奖赏值的马尔可夫过程，其可以用一个四元组表示 \(<S, P, R, \gamma>\)。

• \(S\) 为有限的状态集合；
• \(P\) 为状态转移矩阵，\(P_{ss^{'}} = P[S_{t+1} = s^{'}|S_t = s]\)；
• \(R\) 是奖赏函数；
• \(\gamma\) 为折扣因子（discount factor），其中 \(\gamma \in [0, 1]\)

奖赏函数

在 \(t\) 时刻的奖赏值 \(G_t\)：
\[G_t = R_{t+1} + \gamma R_{t+2} + ... = \sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}\]

Why Discount

关于Return的计算为什么需要 \(\gamma\) 折扣系数。David Silver 给出了下面几条的解释：

• 数学表达的方便
• 避免陷入无限循环
• 远期利益具有一定的不确定性
• 在金融学上，立即的回报相对于延迟的回报能够获得更多的利益
• 符合人类更看重眼前利益的特点

价值函数

状态 \(s\) 的长期价值函数表示为：
\[v(s) = E[G_t | S_t = s] \]

Bellman Equation for MRPs

\[
\begin{align}
v(s)
&= E[G_t|S_t=s]\\
&= E[R_{t+1} + \gamma R_{t+2} + ... | S_t = s]\\
&= E[R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} ... ) | S_t = s]\\
&= E[R_{t+1} + \gamma G_{t+1} | S_t = s]\\
&= E[R_{t+1} + \gamma v(s_{t+1}) | S_t = s]
\end{align}
\]

下图为MRP的 backup tree 示意图：

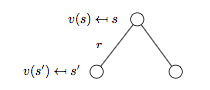
注：backup tree 中的白色圆圈代表状态，黑色圆点对应动作。

根据上图可以进一步得到：
\[v(s) = R_s + \gamma \sum_{s' \in S}P_{ss'}v(s')\]

马尔可夫决策过程

马尔可夫决策过程（Markov Decision Process，MDP）是带有决策的MRP，其可以由一个五元组构成 \(<S, A, P, R, \gamma>\)。

• \(S\) 为有限的状态集合；
• \(A\) 为有限的动作集合；
• \(P\) 为状态转移矩阵，\(P_{ss^{'}}^{a} = P[S_{t+1} = s^{'}|S_t = s,A_t=a]\)；
• \(R\) 是奖赏函数；
• \(\gamma\) 为折扣因子（discount factor），其中 \(\gamma \in [0, 1]\)

我们讨论的MDP一般指有限（离散）马尔可夫决策过程。

策略

策略（Policy）是给定状态下的动作概率分布，即：
\[\pi(a|s) = P[A_t = a|S_t = a]\]

状态价值函数 & 最优状态价值函数

给定策略 \(\pi\) 下状态 \(s\) 的状态价值函数（State-Value Function）\(v_{\pi}(s)\)：
\[v_{\pi}(s) = E_{\pi}[G_t|S_t = s]\]

状态 \(s\) 的最优状态价值函数（The Optimal State-Value Function）\(v_{*}(s)\)：
\[v_{*}(s) = \max_{\pi}v_{\pi}(s)\]

动作价值函数 & 最优动作价值函数

给定策略 \(\pi\)，状态 \(s\)，采取动作 \(a\) 的动作价值函数（Action-Value Function）\(q_{\pi}(s, a)\)：
\[q_{\pi}(s, a) = E_{\pi}[G_t|S_t = s, A_t = a]\]

状态 \(s\) 下采取动作 \(a\) 的最优动作价值函数（The Optimal Action-Value Function）\(q_{*}(s, a)\)：
\[q_{*}(s, a) = \max_{\pi}q_{\pi}(s, a)\]

最优策略

如果策略 \(\pi\) 优于策略 \(\pi^{'}\)：
\[\pi \ge \pi^{'} \text{ if } v_{\pi}(s) \ge v_{\pi^{'}}(s), \forall{s}\]

最优策略 \(v_{*}\) 满足：

• \(v_{*} \ge \pi, \forall{\pi}\)
• \(v_{\pi_{*}}(s) = v_{*}(s)\)
• \(q_{\pi_{*}}(s, a) = q_{*}(s, a)\)

如何找到最优策略？

可以通过最大化 \(q_{*}(s, a)\) 来找到最优策略：
\[
v_{*}(a|s) =
\begin{cases}
& 1 \text{ if } a=\arg\max_{a \in A}q_{*}(s,a)\\
& 0 \text{ otherwise }
\end{cases}
\]

对于MDP而言总存在一个确定的最优策略，而且一旦我们获得了\(q_{*}(s,a)\)，我们就能立即找到最优策略。

Bellman Expectation Equation for MDPs

我们先看下状态价值函数 \(v^{\pi}\)。

状态 \(s\) 对应的 backup tree 如下图所示：

根据上图可得：
\[v_{\pi}(s) = \sum_{a \in A}\pi(a|s)q_{\pi}(s, a) \qquad (1)\]

再来看动作价值函数 \(q_{\pi}(s, a)\)。

状态 \(s\)，动作 \(a\) 对应的 backup tree 如下图所示：

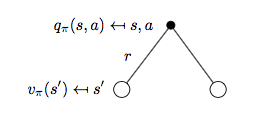
因此可得：
\[q_{\pi}(s,a)=R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a v_{\pi}(s') \qquad (2)\]

进一步细分 backup tree 再来看 \(v^{\pi}\) 与 \(q_{\pi}(s, a)\) 对应的表示形式。

细分状态 \(s\) 对应的 backup tree 如下图所示：

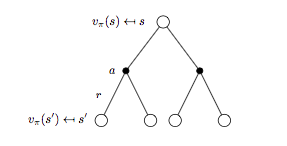
将式子(2)代入式子(1)可以进一步得到 \(v_{\pi}(s)\) 的贝尔曼期望方程：
\[v_{\pi}(s) = \sum_{a \in A} \pi(a | s) \Bigl( R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a v_{\pi}(s') \Bigr) \qquad (3)\]

细分状态 \(s\)，动作 \(a\) 对应的 backup tree 如下图所示：

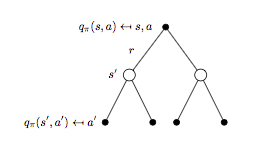
将式子(1)代入式子(2)可以得到 \(q_{\pi}(s,a)\) 的贝尔曼期望方程：
\[q_{\pi}(s,a)=R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a \Bigl(\sum_{a' \in A}\pi(a'|s')q_{\pi}(s', a') \Bigr) \qquad (4)\]

Bellman Optimality Equation for MDPs

同样我们先看 \(v_{*}(s)\)：

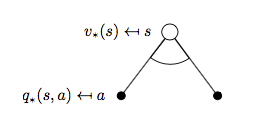
对应可以写出公式：
\[v_{*}(s) = \max_{a}q_{*}(s, a) \qquad (5)\]

再来看\(q_{*}(s, a)\)：

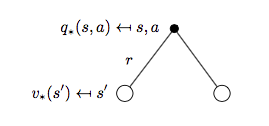
对应公式为：
\[q_{*}(s, a) = R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a v_{*}(s') \qquad (6)\]

同样的套路获取 \(v_{*}(s)\) 对应的 backup tree 以及贝尔曼最优方程：

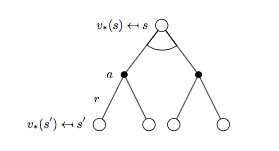
贝尔曼最优方程：
\[v_{*}(s) = \max_{a} \Bigl( R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a v_{*}(s') \Bigr) \qquad (7)\]

\(q_{*}(s, a)\) 对应的 backup tree 以及贝尔曼最优方程：

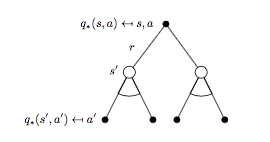
对应的贝尔曼最优方程：
\[R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a\max_{a}q_{*}(s, a) \qquad (8)\]

贝尔曼最优方程特点

• 非线性（non-linear）
• 通常情况下没有解析解（no closed form solution）

贝尔曼最优方程解法

• Value Iteration
• Policy Iteration
• Sarsa
• Q-Learning

MDPs的相关扩展问题

• 无限MDPs/连续MDPs
• 部分可观测的MDPs
• Reward无折扣因子形式的MDPs/平均Reward形式的MDPs

Reference

[1] 维基百科-马尔可夫性
[2] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto, 2018
[3] David Silver's Homepage