【ZJOI 2018】 历史（lct）

历史

题目描述

九条可怜是一个热爱阅读的女孩子。

这个世界有 $n$ 个城市，这 $n$ 个城市被恰好 $n-1$ 条双向道路联通，即任意两个城市都可以互相到达。同时城市 $1$ 坐落在世界的中心，占领了这个城市就称霸了这个世界。

在最开始，这 $n$ 个城市都不在任何国家的控制之下，但是随着社会的发展，一些城市会崛起形成国家并夺取世界的霸权。为了方便，我们标记第 $i$ 个城市崛起产生的国家为第 $i$ 个国家。 在第 $i$ 个城市崛起的过程中，第 $i$ 个国家会取得城市 $i$ 到城市 $1$ 路径上所有城市的控制权。

新的城市的崛起往往意味着战争与死亡，若第 $i$ 个国家在崛起中，需要取得一个原本被国家 $j \; (j \neq i)$ 控制的城市的控制权，那么国家 $i$ 就必须向国家 $j$ 宣战并进行战争。

现在，可怜知道了，在历史上，第 $i$ 个城市一共崛起了 $a_{i}$ 次。但是这些事件发生的相对顺序已经无从考究了，唯一的信息是，在一个城市崛起称霸世界之前，新的城市是不会崛起的。

战争对人民来说是灾难性的。可怜定义一次崛起的灾难度为崛起的过程中会和多少不同的国家进行战争（和同一个国家进行多次战争只会被计入一次）。可怜想要知道，在所有可能的崛起顺序中，灾难度之和最大是多少。

同时，在考古学家的努力下，越来越多的历史资料被发掘了出来，根据这些新的资料，可怜会对 $a_{i}$ 进行一些修正。具体来说，可怜会对 $a_{i}$ 进行一些操作，每次会将 $a_{x}$ 加上 $w$。她希望在每次修改之后，都能计算得到最大的灾难度。

然而可怜对复杂的计算并不感兴趣，因此她想让你来帮她计算一下这些数值。 对题面的一些补充：

• 同一个城市多次崛起形成的国家是同一个国家，这意味着同一个城市连续崛起两次是不会和任何国家开战的：因为这些城市原来就在它的控制之下。
• 在历史的演变过程中，第 $i$ 个国家可能会有一段时间没有任何城市的控制权。但是这并不意味着第 $i$ 个国家灭亡了，在城市 $i$ 崛起的时候，第 $i$ 个国家仍然会取得 $1$ 到 $i$ 路径上的城市的控制权。

输入输出格式

输入格式：

第一行输入两个整数 $n$,$m$ 表示城市个数和操作个数。

第二行输入 $n$ 个整数表示 $a_{i}$ 的初始值。 接下来 $n − 1$ 行，每行输入两个整数 $u_{i}$, $v_{i}$， $(1 \leq u_{i}, v_{i} \leq n)$ 描述了一条道路。

接下来 $m$ 行每行输入两个整数 $x_{i}$, $w_{i}$ 表示将 $a_{x_{i}}$ 加上 $w_{i}$。

输出格式：

输出共 $m+1$ 行，第一行表示初始的 $a_{i}$ 的答案，接下来 $m$ 行每行表示这次修正后的答案。

样例一

input

5 3
1 1 1 1 1
1 2
1 3
2 4
2 5
2 1
3 1
4 1

output

6
7
9
10

explanation

在修正开始之前，如果按照所在城市 $4, 1, 5, 3, 2$ 的顺序崛起，那么依次会和 $0, 1, 2, 1, 2$ 个 国家进行战争。这时一共会产生 $6$ 对敌对关系。可以证明这是所有崛起顺序中的最大值。

限制与约定

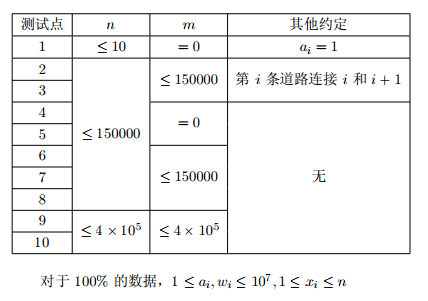
时间限制：2s

空间限制：512MB

可以看出，问题的本质是，给出一棵树，给定每一个点的 $Access$ 次数，计算轻重链切换次数的最大值。

我们假设 $V_{i}$ 为每个节点最多能进行的 $Access$ 次数，$S_{i}$ 为 $i$ 点子树的$V$和。

我们可以先考虑没有修改的情况：

很显然，能改变 $x$ 点向下的边的轻重链的情况，当且仅当 $x$ 的子树中的某个节点进行的 $Access$ 操作。

可以发现，每一个点对答案的贡献是独立的，那设 $A_{x}$ 为 $x$ 点处切换轻重链的最大值，则 $Ans = \sum_{x=1}^{n} A_{x} $。

假设我们已经得到了一组以 $x$ 为子树的点的所有 $Access$ 操作的顺序，那它对 $x$ 点的贡献就是相邻两个点不同属于 $x$ 的某个亲儿子的子树中的数目。

我们可以任意调整它们进行 $Access$ 的顺序使得其贡献最大，设 $x$ 总共有 $m$ 个儿子，因此为了最大化 $x$ 处的轻重链切换次数，问题转化成了，有 $m+1$ 种颜色的小球（算上 $x$ 本身），第 $i$ 种颜色有 $S_{i}$ 个，要求把所有小球摆成一列，最大化左右小球的颜色不同的间隔数。易得，如果最大的某个 $S_{i} * 2$ 不超过 $\sum_{i=1}^{m+1}S_{i} + 1$，我们总能找到一种顺序，使得任意相邻的小球都颜色不同。即 $2 * \max(S_{i}) > \sum_{i=1}^{m+1}S_{i} + 1$ 时，$A_{x}$ 就是 $2*(\sum_{i=1}^{m+1}S_{i} − \max(S_{i}))$，否则 $Ax$ 就是 $\sum_{i=1}^{m+1}S_{i} − 1$。

于是我们可以 $O(n)$ 做无修改的情况了。

现在来考虑有修改的情况：

我们假设 $F$ 是 $i$ 点的父亲，如果 $A_{i} * 2 > A_{F} + 1$，我们就定义这条 $i$ 和 $F$ 的边为实边，否则为虚边。

很容易知道，一个点向下最多只有一条实边（可以类比树剖，虽然不是很一样），有可能没有。

如果我们修改的 $A_{i}$ 的值，则 $i$ 到根的路径上每一个节点的 $S_{i}$ 都会增加，易知，该路径上已经是实边的还会是实边，并且修改不会对实边的贡献造成影响，只要考虑那些虚边在修改后能否变成实边，以及虚边在修改后对答案造成的影响。

我们可以用 $LCT$ 维护该树，只是在 $Access$ 的时候并不是像原先那样切换轻重链，而是直接用虚实边，在原先 $Access$ 切换链的地方判断是否要改变虚实即可。

 #include <cstdio>

 typedef long long LL;

 const int N = ;

 int n, m;
 int L[N], R[N], P[N], hs[N];
 LL Ans, A[N], sum[N], tag[N], va[N];

 int yun, las[N], pre[N<<], to[N<<];
 inline void Add(int a, int b) {
     to[++yun]=b; pre[yun]=las[a]; las[a]=yun;
 }

 inline int Isroot(int x) {
     return L[P[x]]!=x && R[P[x]]!=x;
 }
 inline int Order(int x) {
     return x==R[P[x]];
 }
 inline void Pushdown(int x) {
     if (!tag[x] || !x) return;
     sum[x]+=tag[x]; tag[L[x]]+=tag[x]; tag[R[x]]+=tag[x]; tag[x]=;
 }
 inline void Pushall(int x) {
     if (!Isroot(x)) Pushall(P[x]); Pushdown(x);
 }
 inline void Rotate(int x) {
     int Fa=P[x], Gr=P[Fa], d=Order(x), so=d? L[x]:R[x];
     if (!Isroot(Fa)) (Order(Fa)? R[Gr]:L[Gr])=x; P[x]=Gr;
     (d? R[Fa]:L[Fa])=so; P[so]=Fa;
     (d? L[x]:R[x])=Fa; P[Fa]=x;
 }
 inline void Splay(int x) {
     Pushall(x);
     for (; !Isroot(x); Rotate(x))
         if (!Isroot(P[x])) Rotate(Order(P[x])==Order(x)? P[x]:x);
 }
 inline int Get_root(int x) {
     while (L[x]) Pushdown(x), x=L[x];
     Pushdown(x);
     return x;
 }

 inline void Recalc(int x) {
     Ans-=A[x];
     A[x]=(hs[x])? (*(sum[x]-sum[hs[x]])):(sum[x]-);
     if (va[x]*>sum[x]+) A[x]=*(sum[x]-va[x]);
     Ans+=A[x];
 }

 inline void Access(int x, int y) {
     va[x]+=y;
     for (int t=; x; t=x, x=P[x]) {
         Splay(x);
         sum[x]+=y; tag[L[x]]+=y; Pushdown(L[x]);
         if (hs[x]) {
             Pushall(hs[x]);
             if (sum[hs[x]]*<=sum[x]+) hs[x]=R[x]=;
         }
         int son=Get_root(t);
         if (sum[son]*>sum[x]+) hs[x]=son, R[x]=t;
         Recalc(x);
     }
 }

 void Dfs_pre(int x, int Fa, int Ms=) {
     P[x]=Fa; sum[x]=va[x];
     for (int i=las[x]; i; i=pre[i]) if (to[i]!=Fa) {
         Dfs_pre(to[i], x);
         sum[x]+=sum[to[i]];
         if (!Ms || sum[Ms]<sum[to[i]]) Ms=to[i];
     }
     if (sum[Ms]*>sum[x]+) hs[x]=Ms;
     Recalc(x);
     R[x]=hs[x];
 }

 int main() {
     scanf("%d%d", &n, &m);
     for (int i=; i<=n; ++i) scanf("%lld", &va[i]);
     for (int i=, x, y; i<n; ++i) scanf("%d%d", &x, &y), Add(x, y), Add(y, x);
     Dfs_pre(, );
     printf("%lld\n", Ans);
     for (int x, y; m; --m) scanf("%d%d", &x, &y), Access(x, y), printf("%lld\n", Ans);

     return ;
 }