浅谈Tarjan算法及思想

在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。Tarjan算法有点类似于基于后序的深度遍历搜索和并查集的组合，充分利用回溯来解决问题。

需要注意到Tarjan算法求一个图中的极大强联通子图，强连通分量(strongly connected components)。

比如说，在下例图中中，{1,3,4}与{1,2,3,4}都是符合条件的联通子图，但是{1,3,4}不是强联通分量，因为它不是极大图

所谓极大图，就是子图中包含元素最多的符合所有条件的子图

tarjan算法的具体实现：
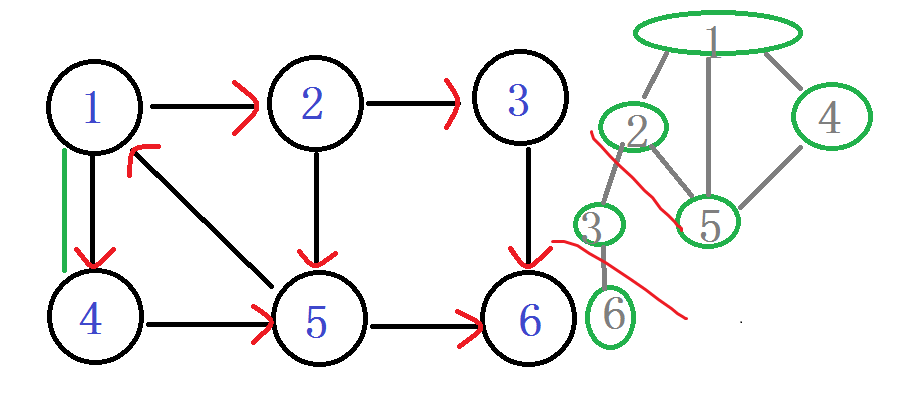
如下图中，强连通分量有：{1,2,3,4}，{5}，{6}

{资料来自于http://blog.csdn.net/jeryjeryjery/article/details/52829142?locationNum=4&fps=1}

可以看到Tarjan算法是依靠一个数据结构——栈来实现的，具体实现的方式上面已经非常清楚了。

下面欣赏一下某dalao的神奇blog，也是比较好的，有错的地方改掉了：

tarjan算法，一个关于 图的联通性的神奇算法。基于DFS（迪法师）算法，深度优先搜索一张有向图。！注意！是有向图。根据树，堆栈，打标记等种种神（che）奇（dan）方法来完成剖析一个图的工作。而图的联通性，就是任督二脉通不通。。的问题。
了解tarjan算法之前你需要知道：
强连通，强连通图，强连通分量，解答树（解答树只是一种形式。了解即可）
不知道怎么办！！！

神奇海螺～：嘟噜噜～！
强连通(strongly connected)： 在一个有向图G里，设两个点 a b 发现，由a有一条路可以走到b，由b又有一条路可以走到a，我们就叫这两个顶点（a，b）强连通。

强连通图： 如果 在一个有向图G中，每两个点都强连通，我们就叫这个图，强连通图。

强连通分量strongly connected components)：在一个有向图G中，有一个子图，这个子图每2个点都满足强连通，我们就叫这个子图叫做 强连通分量 ［分量：：把一个向量分解成几个方向的向量的和，那些方向上的向量就叫做该向量（未分解前的向量）的分量］
举个简单的栗子：

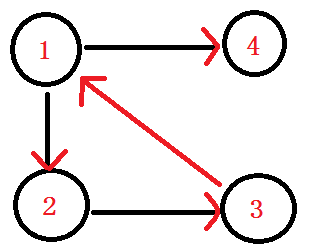
比如说这个图，在这个图中呢，点1与点2互相都有路径到达对方，所以它们强连通.

而在这个有向图中，点1 2 3组成的这个子图，是整个有向图中的强连通分量。

解答树：就是一个可以来表达出递归枚举的方式的树（图），其实也可以说是递归图。。反正都是一个作用，一个展示从“什么都没有做”开始到“所有结求出来”逐步完成的过程。“过程！”

神奇海螺结束！！！

tarjan算法，之所以用DFS就是因为它将每一个强连通分量作为搜索树上的一个子树。而这个图，就是一个完整的搜索树。
为了使这颗搜索树在遇到强连通分量的节点的时候能顺利进行。每个点都有两个参数。
1，DFN［］作为这个点搜索的次序编号（时间戳），简单来说就是 第几个被搜索到的。％每个点的时间戳都不一样％。
2，LOW［］作为每个点在这颗树中的，最小的子树的根，每次保证最小，like它的父亲结点的时间戳这种感觉。如果它自己的LOW［］最小，那这个点就应该从新分配，变成这个强连通分量子树的根节点。
ps：每次找到一个新点，这个点LOW［］＝DFN［］。

而为了存储整个强连通分量，这里挑选的容器是，堆栈。每次一个新节点出现，就进站，如果这个点有 出度 就继续往下找。直到找到底，每次返回上来都看一看子节点与这个节点的LOW值，谁小就取谁，保证最小的子树根。如果找到DFN［］＝＝LOW［］就说明这个节点是这个强连通分量的根节点（毕竟这个LOW［］值是这个强连通分量里最小的。）最后找到强连通分量的节点后，就将这个栈里，比此节点后进来的节点全部出栈，它们就组成一个全新的强连通分量。

先来一段伪代码压压惊：

tarjan(u){
　　DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值
　　Stack.push(u)   // 将节点u压入栈中
　　for each (u, v) in E // 枚举每一条边
　　　　if (v is not visted) // 如果节点v未被访问过
　　　　　　　　tarjan(v) // 继续向下找
　　　　　　　　Low[u] = min(Low[u], Low[v])
　　　　else if (v in S) // 如果节点u还在栈内
　　　　　　　　Low[u] = min(Low[u], DFN[v])
　　if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
　　repeat v = S.pop  // 将v退栈，为该强连通分量中一个顶点
　　print v
　　until (u== v)
 
}

首先来一张有向图。网上到处都是这个图。我们就一点一点来模拟整个算法。

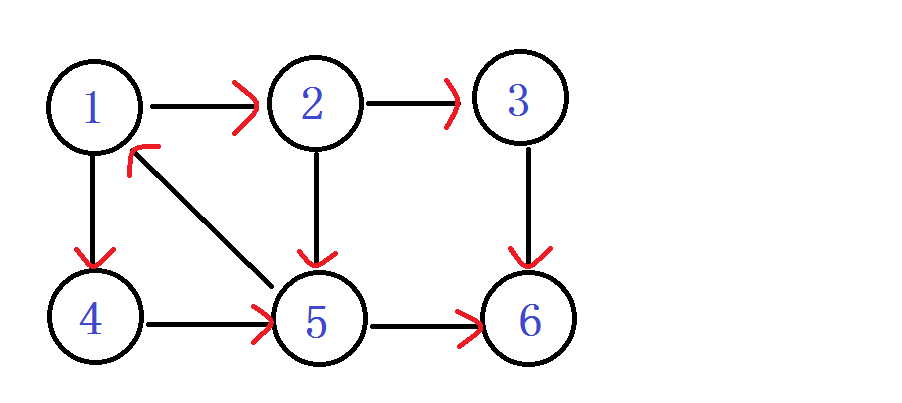
从1进入 DFN［1］＝LOW［1］＝ ＋＋index －－－－1
入栈 1
由1进入2 DFN［2］＝LOW［2］＝ ＋＋index －－－－2
入栈 1 2
之后由2进入3 DFN［3］＝LOW［3］＝ ＋＋index －－－－3
入栈 1 2 3
之后由3进入 6 DFN［6］＝LOW［6］＝＋＋index －－－－4
入栈 1 2 3 6

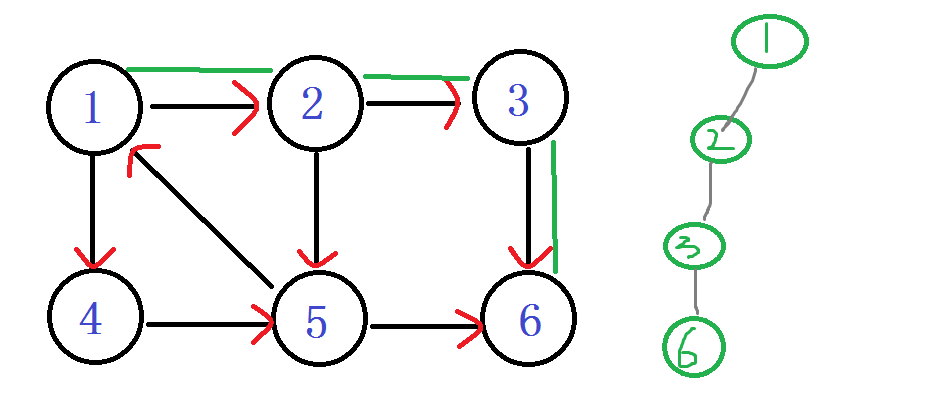
之后发现 嗯？ 6无出度，之后判断 DFN［6］＝＝LOW［6］
说明6是个强连通分量的根节点：6及6以后的点 出栈。
栈： 1 2 3 
之后退回 节点3 Low[3] = min(Low[3], Low[6]) LOW［3］还是 3
节点3 也没有再能延伸的边了，判断 DFN［3］＝＝LOW［3］
说明3是个强连通分量的根节点：3及3以后的点 出栈。
栈： 1 2 
之后退回 节点2 嗯？！往下到节点5
DFN［5］＝LOW［5］＝ ＋＋index －－－－－5
入栈 1 2 5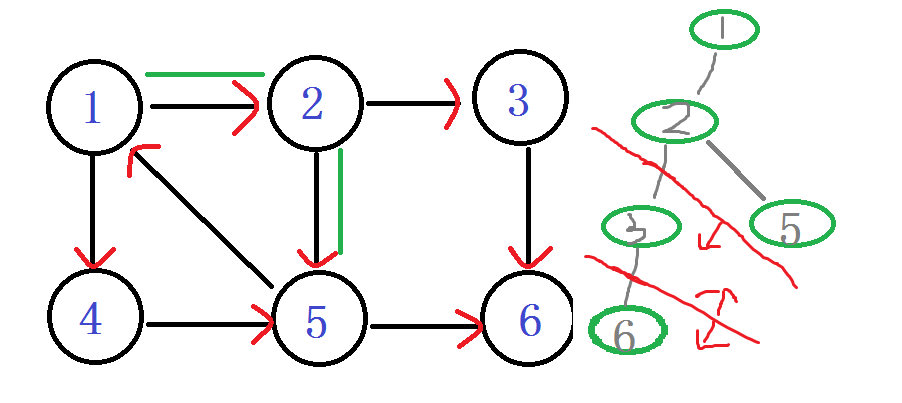

ps：你会发现在有向图旁边的那个丑的（划掉）搜索树 用红线剪掉的子树，那个就是强连通分量子树。每次找到一个。直接。一剪子下去。半个子树就没有了。。

结点5 往下找，发现节点6 DFN［6］有值，被访问过。就不管它。
继续 5往下找，找到了节点1 他爸爸的爸爸。。DFN［1］被访问过并且还在栈中，说明1还在这个强连通分量中，值得发现。 Low[5] = min(Low[5], DFN[1]) 
确定关系，在这棵强连通分量树中，5节点要比1节点出现的晚。所以5是1的子节点。so
LOW［5］＝ 1

由5继续回到2 Low[2] = min(Low[2], Low[5])
LOW［2］＝1；
由2继续回到1 判断 Low[1] = min(Low[1], Low[2]) 
LOW［1］还是 1
1还有边没有走过。发现节点4，访问节点4
DFN［4］＝LOW［4］＝＋＋index －－－－6
入栈 1 2 5 4 
由节点4，走到5，发现5被访问过了，5还在栈里，
Low[4] = min(Low[4], DFN[5]) LOW［4］＝5
说明4是5的一个子节点。

由4回到1.

回到1，判断 Low[1] = min(Low[1], Low[4])
LOW［1］还是 1 。

判断 LOW［1］ ＝＝ DFN［1］ 
诶？！相等了    说明以1为根节点的强连通分量已经找完了。
将栈中1以及1之后进栈的所有点，都出栈。
栈 ：（鬼都没有了）

这个时候就完了吗？！

你以为就完了吗？！

然而并没有完，万一你只走了一遍tarjan整个图没有找完怎么办呢？！

所以。tarjan的调用最好在循环里解决。

like    如果这个点没有被访问过，那么就从这个点开始tarjan一遍。

因为这样好让每个点都被访问到。

来一道裸代码。
 
输入：一个图有向图。
 
输出：它每个强连通分量。

这个图就是刚才讲的那个图。一模一样。

input#1：

6 8
1 2
2 3
3 6
5 6
2 5
5 1
4 5
1 4

output#1：

strongly connected components 1:6
strongly connected components 2:3
strongly connected components 3:2 1 5 4

代码 pascal：（此处是正解）

program Tarjan;
uses math;
const maxn=;
type rec=record
 en,pre,w:longint;
end;
var st,vis:array[-maxn..maxn]of boolean;
    s,dfn,low,head:array[..maxn]of longint;
    tot,cc,i,u,v,w,time,top,n,m,ans:longint;
    a:array[..maxn]of rec;
procedure adde(u,v,w:longint);
begin
 inc(tot);
 a[tot].en:=v;
 a[tot].pre:=head[u];
 head[u]:=tot;
end;
procedure tarjan(u:longint);
var p,v,tt,sum:longint;
begin
 inc(time); dfn[u]:=time; low[u]:=time;
 inc(top); s[top]:=u;
 st[u]:=true;
 p:=head[u];
 while p> do begin
  v:=a[p].en;
   if dfn[v]= then begin
    tarjan(v);
    low[u]:=min(low[u],low[v]);
   end
  else if (dfn[v]<low[u])and(st[v]) then low[u]:=dfn[v];
  p:=a[p].pre;
 end;
 if low[u]=dfn[u] then begin
  if top> then begin
  inc(cc);
  write('strongly connected components ',cc,':');
   sum:=;
  while tt<>u do begin
   tt:=s[top];  write(tt,' ');
   st[tt]:=false;
   dec(top);
   inc(sum);
  end;
  writeln;
  end;
 end;
end;
begin
 readln(n,m);
 for i:= to m do begin
  read(u,v);
  adde(u,v,w);
 end;
 fillchar(vis,sizeof(vis),false);
 fillchar(st,sizeof(st),false);
 //fillchar(use,sizeof(use),false);
 time:=;
 ans:=maxlongint;
 for i:= to n do if dfn[i]= then tarjan(i);
end.

下面是错解（我也不知道拿错了，要不是做了一道luo的Tarjan信息传递我也不知道哪里错了，正解是for循环）

program Tarjan;
uses math;
const maxn=;
type rec=record
 en,pre,w:longint;
end;
var st,vis,use:array[-maxn..maxn]of boolean;
    s,dfn,low,head:array[..maxn]of longint;
    tot,cc,i,u,v,w,time,top,n,m:longint;
    a:array[..maxn]of rec;
procedure adde(u,v,w:longint);
begin
 inc(tot);
 a[tot].en:=v;
 a[tot].pre:=head[u];
 head[u]:=tot;
end;
procedure tarjan(u:longint);
var p,v,tt:longint;
begin
 inc(time); dfn[u]:=time; low[u]:=time;
 inc(top); s[top]:=u;
 st[u]:=true;
 p:=head[u];
 while p> do begin
  v:=a[p].en;
  if not use[v] then begin
   use[v]:=true;
   tarjan(v);
   low[u]:=min(low[u],low[v]);
  end
  else if (dfn[v]<low[u])and(st[v]) then low[u]:=dfn[v];
  p:=a[p].pre;
 end;
 if low[u]=dfn[u] then begin
  if top> then begin
  inc(cc);
  write('strongly connected components ',cc,':');
  while tt<>u do begin
   tt:=s[top];  write(tt,' ');
   st[tt]:=false;
   dec(top);
  end;
  writeln;
  end;
 end;
end;
begin
 readln(n,m);
 for i:= to m do begin
  readln(u,v);
  adde(u,v,w);
 end;
 fillchar(vis,sizeof(vis),false);
 fillchar(st,sizeof(st),false);
 fillchar(use,sizeof(use),false);
 time:=;
 tarjan();
end.