【Coursera】线性回归和逻辑回归

一、线性回归

1、批量梯度下降法

• 每次对参数进行一次迭代时，都要扫描一遍输入全集
• 算法可以收敛到局部最优值
• 当迭代多次之后，每次迭代参数的改变越小

2、随机梯度下降法

• 对于一个输入样本，对参数进行一次更新
• 算法通常不会收敛到局部最优值，整个过程类似在上山迂回下山，有时可能上山，有时可能下山，但算法的最后都会得到局部最优值附近的一个值
• 若输入数据非常多的时候，随机梯度下降比批量梯度下降更加合适

3、概率解释

　　在原式子里加入一个"error term"，之后得到这个“error tem”的正态分布，从而到处输出y和x、θ之间的概率关系。然后通过最大似然估计法，得到若要使得y的概率最大，等价于利用最小二乘法最小化θ。

二、局部加权线性回归

1. 参数θ的数量随着训练数据的增大而变多，但是当训练数据量巨大的时候，每次预测所需要的代价都很高。
2. 原训练数据需要保留，因为每当对一个新的数据X进行预测时，需要用到X周围的测试数据，从而得出θ的值。对于和测试点靠近的训练点数据，所得权值较高，而对于距离测试点很远的测试数据，所得权值就很小，这就是为什么叫做局部线性回归的原因。
3. 对于线性回归，，利用训练数据求出θ之后，在对一个新的数据进行预测时，将不会再使用到原训练数据
4. 局部加权线性回归是一种非参数学习算法，而线性回归是一种参数学习算法。

三、逻辑回归

1. 核心在于使用了sigmod函数，使得函数输出的值分布在[0, 1]区间内。
2. 在某些特定条件下，为了使得sigmod函数g(z)的输出为两个离散值：0和1.可以使用感知器学习算法。
3. 逻辑回归推导到最后的公式形式和线性回归中的最小二乘形式几乎相同，但是它们属于不同的算法，因为h(θ)函数不同，导致了根本的差异。

四、牛顿法

1. 在对参数θ进行极大似然估计时，可以采用Newton’s method。这个算法收敛的速度非常快（二次收敛），迭代次数也少，但是在每次迭代时，都需要计算一次Hessian矩阵，计算量和n有关。因此当量级偏少少，牛顿迭代法也是一个相当好的算法。
2. 参数的数值可以任取，但是一般取为零向量。
3. 海森价值函数: \(J(\Theta )=\frac{1}{2}\sum_{i=1}^{m}(\Theta ^{T}x^{(a)} - y^{i})^{2}\) \(H=X^{T}X\)
4. 无论θ的初始值为什么，牛顿法迭代一次后即可得到：\(\Theta^{*}=(X^{T}X)^{-1}X^{T}\vec{y}\), 即最小二乘法的解。

五、广义线性模型

1. 线性回归和逻辑回归中的伯努利分布和高斯分布都可以转换为指数分布的形式。
2. 在将伯努利分布转换为指数分布的过程中，可以得到sigmod函数，这就是之前为什么Logisitic regression刚好是sigmod函数的原因。（当然，还有更深层次的原因）

六、回归问题实战

1、线性回归

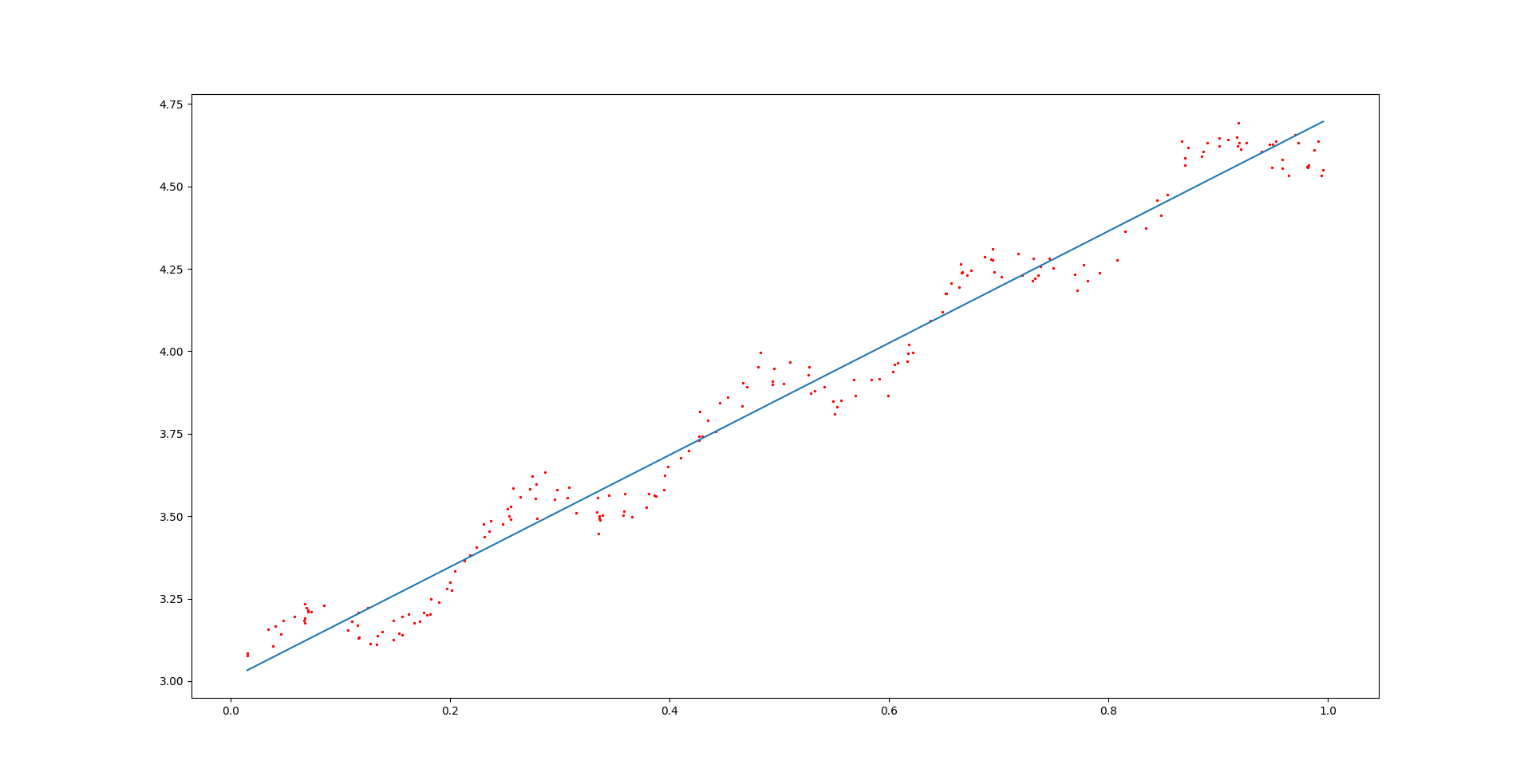
2、局部加权回归（参数0.01）

　　局部加权回归中，参数设定非常重要，可能存在欠拟合和过拟合的情况。

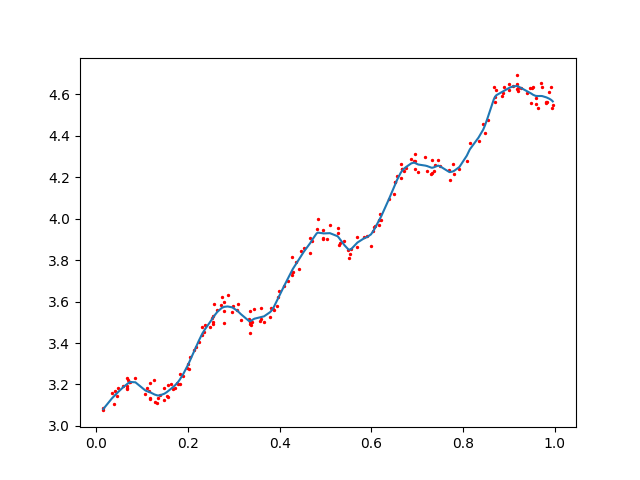
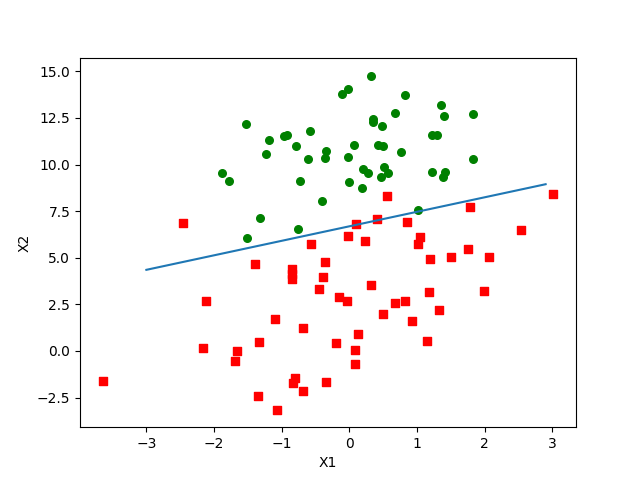
3、逻辑回归

　　参数θ的有多种更新方法——梯度下降法和牛顿法等，务必掌握其优缺点，合理选用。