Monty Hall 问题与贝叶斯定理的理解

 三门问题（Monty Hall problem），是一个源自博弈论的数学游戏问题，大致出自美国的电视游戏节目Let's Make a Deal。问题的名字来自该节目的主持人蒙提·霍尔（Monty Hall）。

游戏规则

游戏参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门就可以赢得该汽车，而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人会开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机会率？

我们假设三扇门为A、B、C。那么对于参赛者而言，刚开始做出选择的时候P(A)=P(B)=P(C)=1/3。

现在我们假设选定一个门A，那么剩下的B、C门会被主持人打开一个，P（D）为打开B或C们的概率为1/2。

现在主持人会问是否换一扇门。如果坚持不换，坚持打开A门。P（A|D）=P（AD）/P（D）=1/3。参赛者选择的还是最初的门，在这里主持人是否开启一扇门，对最初的1/3概率没有影响。

如果不坚持选择A门，那么BC两扇门中存在汽车的可能性为P(E)=2/3，且其中一扇门被主持人打开，确定没有汽车只有山羊。假设换一扇门打开的概率为P（E|D）=P(ED)/P(D)=2/3

有一人认为在主持人选了一个门之后  另外两个门概率对我们来说是二分之一。这种想法是有问题的。如果选择坚持A，那么主持人的选择对我们获得汽车的概率是没有影响的，我们还是之前的三分之一概率。如果选择换一扇门选择另一个门C，二分之一是针对只有2扇门的情况下的概率，但是在此之前发生了一个B门被主持人打开的事件。B也是样本元素之一。整个样本元素的数量为3。所以不坚持A的话。必须将B也考虑进去，BC有车的概率为三分之二。

贝叶斯定理由英国数学家贝叶斯 ( Thomas Bayes 1702-1761 ) 发展，用来描述两个条件概率之间的关系，比如 P(A|B) 和 P(B|A)。按照乘法法则，可以立刻导出：P(A∩B) = P(A)*P(B|A)=P(B)*P(A|B)。如上公式也可变形为：P(B|A) = P(A|B)*P(B) / P(A)。

这个问题用贝叶斯定理来理解就有点绕比较简单了。

先来看看贝叶斯公式

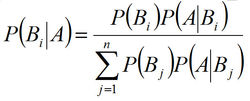
我们首先设定以下三个随机事件：

A：所选的X号门后是汽车。

B：换门后，当前门后是汽车

C：你选择了X号门，而主持人打开了y号门并且y号门后面是山羊。

如果坚持不换门的情况下，我们的目标是P（A|C），即在得到主持人信息之后1号门后是汽车的概率。在主持人提供信息之前，我们有P（A）=1/3。

D发生的几率，仔细想想是1/2，因为主持人会随机的打开一扇门后有羊的门。

这个地方的1/2 ×2/3=1/2 × 1/3 +1/2 × 1/3

换门的话，我们的目标是P(B|C), 此时P（C）的概率就变成了1,是必然事件了

根据贝叶斯公式就可求得结果是2/3

这游戏相当于你和主持人博弈，你只能选一扇门，主持人就选剩下的两扇门。显然主持人的胜率是2/3。这个胜率和主持人是否打开一扇门没有关系，和主持人是否知道门里有没有奖也没有关系，都是你自己先选的啊！

现在给你一个机会，用你手里的一扇门交换主持人手里的两扇门，你换不换？

人们根据不确定性信息作出推理和决策需要对各种结论的概率作出估计。Monty Hall与贝叶斯定理不仅包含了概率学和逻辑学，还包含了心理学，但研究的角度是不同的。心理学研究人们主观概率估计的认知加工过程规律。这一领域的探讨对揭示人们对概率信息的认知加工过程与规律、指导人们进行有效的学习和判断决策都具有十分重要的理论意义和实践意义。在机器学习中包含了各种对数据的判断与决策。因此贝叶斯定理在机器学习中也起着至关重要的作用。

我觉得贝叶斯定理给我的启示就是：不要主观的去对一个问题进行定义，需要结合影响这个问题的其他事件一起来看待。理性且全面的认知一个问题。