Method for balancing binary search trees

Method for balancing a binary search tree. A computer implemented method for balancing a binary search tree includes locating a node in a binary search tree, determining whether a depth of the located node is greater than a threshold, and performing balancing operations. If the depth of the located node is greater than the threshold, the balancing operations may include a modified semi-splay balancing procedure. Regardless of depth, localized balancing operations may be performed while locating a node.

BACKGROUND OF THE INVENTION

1. Field of the Invention

The present invention relates generally to the data processing field, and more particularly, to a method for balancing a binary search tree.

2. Description of the Related Art

A binary search tree is a data structure for representing tables and lists so that items in the tables or lists can be easily accessed, added and deleted. A binary search tree contains a set of the items in a particular table or list, with one item per node of the tree. The items are arranged on the tree in a symmetric order. For example, if a node x of the tree contains a specific item i, the left sub-tree of x will contain items less than item i, and the right sub-tree will contain items greater than item i.

When a binary search tree becomes unbalanced, the time required to do a look-up can increase significantly. For example, a project that may require only seconds to complete using a balanced tree may require minutes or even hours to complete with an unbalanced tree. As a result, balancing a binary search tree is an important and pervasive problem, and many solutions have been proposed over the years. In general, however, the proposed solutions are non-optimal in that they often perform differently on different workloads and frequently introduce significant overhead.

One mechanism for improving efficiency in balancing a binary search tree is to use a self-adjusting data structure in which a restructuring rule is applied during each operation in order to improve the efficiency of future operations. The publication "Self Adjusting Binary Search Trees", Daniel Dominic Sleator and Robert Endre Tarjan, Journal of the Association for Computing Machinery, Vol. 32, No. 3, July, 1985, pp. 652-686, hereinafter referred to as "Sleator", describes a self-adjusting form of binary search tree referred to as a "splay" tree. The heuristic used in restructuring a splay tree is referred to as "splaying", and involves balancing a tree by moving an accessed node to the root of the tree by performing a sequence of rotations bottom-up along a path from the node to the root. The "bottom-up splaying process" is described in detail in the publication.

Sleator also recognizes that a possible drawback of splaying is that the process requires a large amount of restructuring; and, thus, significantly increases overhead. Sleator therefore proposes modifying the restructuring rules of the splaying process to move the accessed node only part way to the root. This balancing process is referred to as "bottom-up semisplaying", and has the effect of reducing the depth of every node on the access path to, at most, about half of its previous value. Although bottom-up semisplaying can provide a reduction in overhead as compared to splaying, it is still computationally intensive.

There is, accordingly, a need for a mechanism for balancing a binary searchtree that is effective in substantially all environments, and that reduces the overhead involved in balancing a tree.

SUMMARY OF THE INVENTION

The present invention provides a method for balancing a binary search tree. A computer implemented method for balancing a binary search tree includes locating a node in a binary search tree, determining whether a depth of the located node is greater than a threshold, and performing balancing operations. If the depth of the located node is greater than the threshold, the balancing operations may include a modified semi-splay balancing procedure. Regardless of depth, localized balancing operations may be performed while locating a node.

BRIEF DESCRIPTION OF THE DRAWINGS

The novel features believed characteristic of the invention are set forth in the appended claims. The invention itself, however, as well as a preferred mode of use, further objectives and advantages thereof, will best be understood by reference to the following detailed description of an illustrative embodiment when read in conjunction with the accompanying drawings, wherein:

FIG. 1 depicts a pictorial representation of a network of data processing systems in which aspects of the present invention may be implemented;

FIG. 2 depicts a block diagram of a data processing system in which aspects of the present invention may be implemented;

FIGS. 3-11 are diagrams that schematically illustrate steps for balancing abinary search tree comparing known bottom-up semi-splay balancing procedures with modified bottom-up semi-splay balancing procedures according to exemplary embodiments of the present invention;

FIGS. 12-15 are diagrams that schematically illustrate complementary and independent balancing rules for balancing a binary search tree according to exemplary embodiments of the present invention; and

FIG. 16 is a flowchart that illustrates a method for balancing a binary searchtree according to an exemplary embodiment of the present invention.

DETAILED DESCRIPTION OF THE PREFERRED EMBODIMENT

FIGS. 1-2 are provided as exemplary diagrams of data processing environments in which embodiments of the present invention may be implemented. It should be appreciated that FIGS. 1-2 are only exemplary and are not intended to assert or imply any limitation with regard to the environments in which aspects or embodiments of the present invention may be implemented. Many modifications to the depicted environments may be made without departing from the spirit and scope of the present invention.

The present invention provides a method for balancing a binary search tree in a data processing system, such as, for example, data processing systems 100 and 200 illustrated in FIGS. 1 and 2. Certain exemplary embodiments of the present invention provide a "modified bottom-up semi-splaying" process for balancing binary search trees, and build upon the concepts and procedures described in the Sleator publication referenced above. Other exemplary embodiments of the invention are independent in origin and can be used on their own or in combination with other balancing techniques such as modified bottom-up semi-splaying.

In order to assist in understanding the present invention, it is important to understand the three primary design goals met by the invention:

• Goal 1 Trees that do not need balancing should have no balancing operations performed on them;
• Goal 2 Determining if a tree does not need balancing should be a low cost, constant overhead; and
• Goal 3 Trees do not need to be perfectly balanced, but should be reasonably balanced and avoid degenerative unbalance.

The present invention modifies the algorithms described in Sleator and provides new complementary but independent algorithms to provide a series of improvements that achieves the above design goals.

In accordance with exemplary embodiments of the present invention, Goal 1 is achieved by triggering tree manipulations only when a tree becomes unreasonably unbalanced. Achieving this goal requires defining and monitoring "unreasonably unbalanced", and the present invention achieves Goal 2 by providing a mechanism that does so in an efficient, low cost manner. Goal 3 is achieved by a first mechanism that improves the amount a semi-splay sequence restores balance to a tree by reducing the number of times semi-splay operations are needed to reduce imbalance, and a second mechanism that complements the first mechanism to further improve tree balance, particularly in a worst case scenario.

As indicated above, a modified semi-splay tree balancing operation is performed only when a tree becomes abnormally unbalanced, i.e., when there is an abnormally long access to an item in the tree. Additionally, the present invention determines when a tree should be balanced by a mechanism that is low in cost and that has a constant overhead.

The ideal maximum weight of a perfectly balanced binary tree is defined by cieling (lg(n)), which can be performed in two very fast assembly instructions on Power PC, clz (count leading zeros) and sub (subtract). A simple counter during anysearch of the tree will determine the weight w(i) of the item being searched. A simple counter that is incremented when items are inserted and decremented when items are removed will determine n. Thus, according to an exemplary embodiment of the present invention, splaying is performed when the weight of the item being searched w(i)>=c* cieling(lg(n))+e. Although semi-splaying can be performed at any desired depth without departing from the scope of the invention, inasmuch as semi-splay reduces the depth of the nodes by about half, as indicated previously, it is generally desirable to semi-splay when the depth is about double the ideal depth. This has been confirmed by experimentation setting c=1 and e=lg(n). Additional tuning can also be done with this equation. For example, e could be expanded to be max (5, lg(n)) to impose minimum heuristics.

Once it is determined that a splaying operation should be performed to balance an unreasonably unbalanced binarysearch tree; various balancing procedures are performed depending on the item being accessed, its relationship with respect to the root of the tree, and on other factors. Some of these procedures are the same as disclosed in Sleator, while others differ from Sleator in such a way as to improve the overall balancing process. FIGS. 3-11 are diagrams that schematically illustrate steps for balancing a binary search tree comparing known bottom-up semi-splay balancing procedures with modified bottom-up semi-splay balancing procedures according to exemplary embodiments of the present invention.

FIGS. 3-6 schematically illustrate known balancing procedures described in Sleator for cases wherein the parent y of an item x being accessed is the tree root. In such cases, the edge joining x with y is rotated (this is referred to as a "zig" in Sleator). Specifically, FIG. 3 illustrates a process of left rotating the sub-tree spanned by the given node x, and FIG. 4illustrates the root case for the left rotation to move node x to the root of the tree. Similarly, FIG. 5 illustrates right rotating the sub-tree spanned by the given node x, and FIG. 6 illustrates the root case for the right rotation to move node x to the root of the tree. It should be noted that the zig operations illustrated in FIGS. 4 and 6 are the same as those illustrated and described in Sleator, and are also used in similar situations to balance a binary search tree in the present invention.

FIGS. 7-8 schematically illustrate the case wherein the parent y of the node x being accessed is not the tree root, and wherein x and y are left children of the tree root z. In particular, FIG. 7 illustrates a standard semi-splay operation described in Sleator in which the edge joining the parent y with the grandparent z is rotated, and then the edge joining x with y is rotated (this is referred to as a "zig-zig" operation in Sleator).

It is relatively common, however, where the parent's right child is NULL (i.e., does not contain an item) and the grandparent's right child is not NULL as shown in FIG. 8. In this case, as shown in FIG. 8, and according to an exemplary embodiment of the present invention, it is better to rotate on y, the parent of x, and promote z, the grandparent. This maintains the semi-splay properties, but is more efficient than the standard semi-splay zig-zig operation illustrated in FIG. 7. In this modification, sub-tree T1 has its weight reduced by 1, sub-trees T2 and T4 remain unchanged, and the only weight increase occurs in the NULL sub-tree. The average and maximum depth are guaranteed to not worsen, and if T1 is not NULL, it is guaranteed to improve.

FIG. 9 illustrates a zig-zag procedure for balancing a binary tree as described in Sleator. As explained in Sleator, this procedure is followed when y is not the root, x is the left child and y the right child or vice versa. In the procedure, the edge joining x with y is rotated, and then the edge joining x with the new y is rotated. FIG. 10 illustrates a zag-zag procedure described in Sleator and comprises the mirror of the procedure illustrated in FIG. 7.

FIG. 11 illustrates a zag-zag procedure for balancing a binary tree, according to an exemplary embodiment of the present invention that improves on the zag-zag procedure illustrated in FIG. 10 in the case where y's left child is a NULL and z's left child is not a NULL. It should be noted that the procedure shown in FIG. 11 is a mirror of the procedure illustrated inFIG. 8, and in this case also, it is better to rotate on y, the parent of x, and promote z, the grandparent.

In general, experimentation has proven the balancing procedures illustrated in FIGS. 8 and 11 to be quite successful. The procedures have produced trees which are more balanced as judged by maximum depth in all tested workloads as compared to when conventional semi-splay procedures are used. The procedures require no extra rotations, and only an extra comparison or two on data which has already been fetched. The better balance achieved by the balancing procedures illustrated in FIGS. 8 and 11 can cut down on the number of semi-splay operations that would otherwise be required, resulting in an increase in performance. Furthermore, the better balance achieved cuts down on the number of comparisons needed to search or insert, which also increases performance.

The balancing algorithm described above runs very rarely and is very tolerant to the tree being improved underneath it. As a result, additional improvements that run independently of the semi-splay process can also be provided so long as they do not interfere with the effectiveness of semi-splay.

Every time a search of or insert into a binary search tree is performed, on the order of lg(n) nodes are looked at. According to further exemplary embodiments of the invention, the information that is gathered is used to further improve binary tree balancing. In particular, it has been recognized that by looking at only the last three nodes along the access path, situations can be identified where the tree can be made better (i.e., how the total weight and maximum individual weight of the tree can be improved). The procedure is very inexpensive, and often very effective.

FIGS. 12-15 are diagrams that schematically illustrate complementary and independent balancing rules for balancing abinary search tree according to exemplary embodiments of the present invention. It should be understood that the balancing rules illustrated in FIGS. 12-15, and referred to herein as "no uncle load balancing", are independent of the semi-splay procedures described in Sleator and of the modified semi-splay procedures described above. They can be used on their own, if desired, or in combination with other balancing techniques such as the modified bottom-up semi-splaying technique described with reference to FIGS. 3-11.

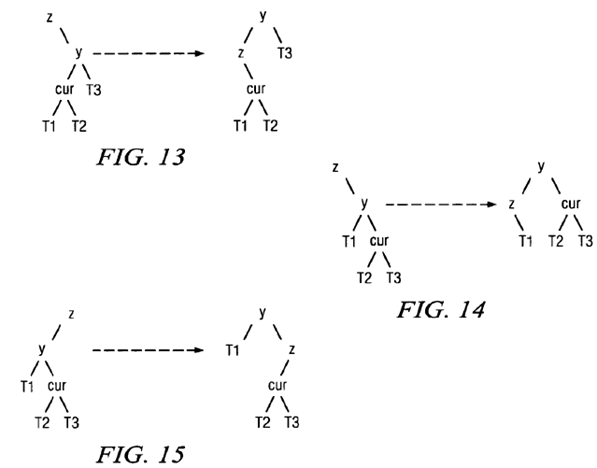
FIG. 12 illustrates a no uncle load balancing procedure for a zig-zig operation in which the grandparent has a NULL child.FIG. 13 illustrates the procedure for a zig-zag operation where the grandparent has a NULL child (this operation should not be performed, however, if T3 in FIG. 13 is not an actual tree since it is all that gets promoted).

FIG. 14 is a mirror case of FIG. 12 and illustrates the no uncle load balancing operation in the case of a zag-zag operation where the grandparent has a NULL for its other child; and FIG. 15 is the mirror case of FIG. 13 and illustrates a zag-zig operation where the grandparent has a NULL for its other child.

FIG. 16 is a flowchart that schematically illustrates a method for balancing a binary search tree according to an exemplary embodiment of the present invention. The method is generally designated by reference number 1600, and includes steps for determining when a node of a binary search tree should be balanced, and for thereafter performing a balancing operation.

The method begins by searching for a node in a binary search tree in a conventional manner, while keeping track of depth as the search is performed (Step 1602). The process is continued until a node is found (Step 1604). A determination is then made whether the node depth is greater than a threshold (Step 1606). If the node depth is not greater than the threshold (No output of Step 1606), the method ends for that node. If the node depth is greater than the threshold (Yes output of Step 1606), a balancing operation is performed on the node (Step 1608). Step 1608 may include the modified bottom-up semi-splaying balancing procedures described with reference to FIGS. 3-11 and may be performed alone or in conjunction with the no uncle load balancing procedures described with reference to FIGS. 12-15, which can be performed in conjunction with Step 1602. The no uncle load balancing operation may also be performed alone or in conjunction with other tree balancing procedures.

The present invention thus provides a method for balancing a binary search tree. A computer implemented method for balancing a binary search tree includes locating a node in a binary search tree, determining whether a depth of the located node is greater than a threshold, and performing balancing operations. If the depth of the located node is greater than the threshold, the balancing operations may include a modified semi-splay balancing procedure. Regardless of depth, localized balancing operations may be performed while locating a node.

SRC=https://www.google.com.hk/patents/US7447698