定理1.24 (棣莫弗定理)

对每个实数x和每个正整数n有

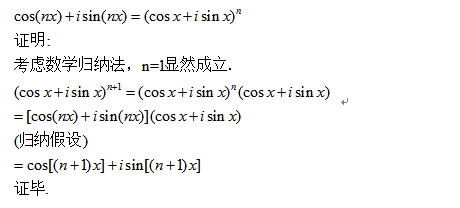
基于棣莫弗定理的推论如下：

《A First Course in Abstract Algebra with Applications》-chaper1-数论-棣莫弗定理的更多相关文章

  1. 《A First Course in Abstract Algebra with Applications》-chaper1-数论

    由于笔者在别的专栏多次介绍过数论,这里在<抽象代数基础教程>的专栏下,对于chaper1数论这一章节介绍的方式不那么“入门”. 首先来介绍一个代数中常用也是非常重要的证明方法:数学归纳法. ...

  2. 《A First Course in Abstract Algebra with Applications》-chaper1-数论-关于素数

    由于笔者在别的专栏多次介绍过数论,这里在<抽象代数基础教程>的专栏下,对于chaper1数论这一章节介绍的方式不那么“入门”. 首先来介绍一个代数中常用也是非常重要的证明方法:数学归纳法. ...

  3. In abstract algebra, a congruence relation (or simply congruence) is an equivalence relation on an algebraic structure (such as a group, ring, or vector space) that is compatible with the structure in

    https://en.wikipedia.org/wiki/Congruence_relation In abstract algebra, a congruence relation (or sim ...

  4. 线性代数 -- Linear Algebra with Applications

    @.如果线性方程组无解,则称该方程组是不相容的(inconsistent). @.如果线性方程组至少存在一个解,则称该方程组是相容的(consistent). @.等价方程组(equivalent s ...

  5. Abstract Algebra chapter 7

    7.7:Encrypt each of the following RSA messages x so that x is divided into blocks of integers of len ...

  6. 浅谈FFT（快速傅里叶变换）

    前言 啊摸鱼真爽哈哈哈哈哈哈 这个假期努力多更几篇( 理解本算法需对一些< 常 用 >数学概念比较清楚,如复数.虚数.三角函数等(不会的自己查去(其实就是懒得写了(￢︿̫̿￢☆) 整理了一 ...

  7. Mathematics for Computer Graphics数学在计算机图形学中的应用 [转]

    最近严重感觉到数学知识的不足! http://bbs.gameres.com/showthread.asp?threadid=10509 [译]Mathematics for Computer Gra ...

  8. 数学类杂志SCI2013-2014影响因子

    ISSN Abbreviated Journal Title Full Title Category Subcategory Country total Cites IF        2013-20 ...

  9. Mathematics for Computer Graphics

    Mathematics for Computer Graphics 最近严重感觉到数学知识的不足! http://bbs.gameres.com/showthread.asp?threadid=105 ...

随机推荐

  1. 我的寒假C（C++）学习计划

    前言 要补缺加强C语言的想法由来已久,上学期因为种种原因,某些知识点学习得不是很理想,而且,许多地方也有加强的必要,所以这次布置的随笔可谓是来得恰到好处. 学习材料 C Primer Plus 师爷的 ...

  2. b5

    吴晓晖(组长) 过去两天完成了哪些任务 完善推荐算法 展示GitHub当日代码/文档签入记录 接下来的计划 推荐算法 还剩下哪些任务 组员:刘帅珍 过去两天完成了哪些任务: 修改原型,整理背景 明日计 ...

  3. golang type

    参考链接 https://blog.csdn.net/tzs919/article/details/53571632 type是golang中非常重要的关键字,常见的就是定义结构体,但是其功能远不止是 ...

  4. SQL Server 2008 存储过程示例

    出处:http://www.jb51.net/article/54730.htm --有输入参数的存储过程-- create proc GetComment (@commentid int) as s ...

  5. Gradle入门（6）：创建Web应用项目

    如果要用 Java 和 Gradle 创建一个 Web 应用项目,我们首先需要创建一个 Java 项目,下面来看看该如何去做. 创建Java项目 我们可以使用Java插件创建一个Java项目,通过添加 ...

  6. Alpha阶段敏捷冲刺⑤

    1.提供当天站立式会议照片一张. 每个人的工作 (有work item 的ID),并将其记录在码云项目管理中: 昨天已完成的工作. 新增了一个登录界面 完成记账的分类模块 报表界面初步设计 今天要完成 ...

  7. 软工网络15团队作业8——Beta阶段敏捷冲刺（用户使用调查报告）

    一.项目概述 1.项目名称 考研必背 2.项目简介 微信小程序,帮助考研学生记忆单词. 3.项目预期达到目标 用户无需下载app,仅通过微信小程序就可以达到背单词的目的,并且能够制定背单词的计划. 4 ...

  8. XMind2TestCase：一个高效测试用例设计的解决方案！

    一.背景 软件测试过程中,最重要.最核心就是测试用例的设计,也是测试童鞋.测试团队日常投入最多时间的工作内容之一. 然而,传统的测试用例设计过程有很多痛点: 1.使用Excel表格进行测试用例设计,虽 ...

  9. InvalidArgumentError: You must feed a value for placeholder tensor 'Placeholder_1' with dtype float and shape [?,10]

    在莫烦Python教程的“Dropout 解决 overfitting”一节中,出现错误如下: InvalidArgumentError: You must feed a value for plac ...

  10. 【Java并发编程】之十：使用wait/notify/notifyAll实现线程间通信的几点重要说明

    在Java中,可以通过配合调用Object对象的wait()方法和notify()方法或notifyAll()方法来实现线程间的通信.在线程中调用wait()方法,将阻塞等待其他线程的通知(其他线程调 ...