BZOJ 2333: [SCOI2011]棘手的操作 可并堆 左偏树 set

https://www.lydsy.com/JudgeOnline/problem.php?id=2333

需要两个结构分别维护每个连通块的最大值和所有连通块最大值中的最大值，可以用两个可并堆实现，也可以用一个可并堆一个平衡树实现，我看的题解用了内置红黑树的set，更加方便，所以我也用了set。

set的用法：https://blog.csdn.net/yas12345678/article/details/52601454 需要注意的是set的find和erase之类的操作返回输入的都是指针，在最后找最大值时，返回的是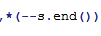，也是指针实现的。

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #include<set>
 using namespace std;
 const int maxn=;
 multiset<int>s;
 int n,q;
 int fa[maxn]={},rt[maxn]={},ch[maxn][]={},cnt[maxn]={},add[maxn]={},val[maxn]={},zong=;
 char op[]={};
 inline void downdata(int x){
     if(ch[x][]){val[ch[x][]]+=add[x];add[ch[x][]]+=add[x];}
     if(ch[x][]){val[ch[x][]]+=add[x];add[ch[x][]]+=add[x];}
     add[x]=;
 }
 void updata(int x){//这里的updata是把上面的所有标记传递下来
     if(fa[x])updata(fa[x]);
     downdata(x);
 }
 int merge(int x,int y){
     if(!y)return x;
     if(!x) return y;
     downdata(x);downdata(y);
     if(val[x]<val[y])swap(x,y);
     ch[x][]=merge(ch[x][],y);fa[ch[x][]]=x;
     if(ch[x][]<ch[x][])swap(ch[x][],ch[x][]);
     cnt[x]=cnt[ch[x][]]+;
     return x;
 }
 int Find(int x){
     return fa[x]?Find(fa[x]):x;
 }
 inline int cle(int x){//把x与他的父亲儿子断绝关系，return堆顶
     int t=merge(ch[x][],ch[x][]),y=fa[x];
     fa[x]=ch[x][]=ch[x][]=;
     if(x==ch[y][])ch[y][]=t;
     if(x==ch[y][])ch[y][]=t;
     fa[t]=y;
     return Find(t);
 }
 inline void del(int x){
     s.erase(s.find(x));
 }
 int main(){
     scanf("%d",&n);
     for(int i=;i<=n;i++){scanf("%d",&val[i]);s.insert(val[i]);}
     scanf("%d",&q);int x,y,xx,yy;
     for(int i=;i<=q;i++){
         scanf("%s",op);
         if(op[]=='A'){
             scanf("%d",&x);
             if(op[]==''){
                 scanf("%d",&y);
                 updata(x);del(val[Find(x)]);val[x]+=y;
                 s.insert(val[merge(x,cle(x))]);
             }
             else if(op[]==''){
                 scanf("%d",&y);
                 xx=Find(x);del(val[xx]);add[xx]+=y;val[xx]+=y;
                 s.insert(val[xx]);
             }
             else zong+=x;
         }
         else if(op[]=='F'){
             if(op[]==''){
                 scanf("%d",&x);updata(x);printf("%d\n",val[x]+zong);
             }
             else if(op[]==''){
                 scanf("%d",&x);
                 printf("%d\n",val[Find(x)]+zong);
             }
             else{
                 printf("%d\n",*(--s.end())+zong);
             }
         }else{
             scanf("%d%d",&x,&y);
             yy=Find(y);xx=Find(x);
             if(xx!=yy){
                 if(merge(xx,yy)==xx)del(val[yy]);
                 else del(val[xx]);
             }
         }
     }
     return ;
 }

可并堆+set

这道题的另一个写法是离线+线段树，将所有需要并到一起的点离线处理编号在线段树上放到一起，也很清晰。

这里将点排序的方法大概是桶排序？

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #include<set>
 using namespace std;
 #define lc x*2
 #define rc x*2+1
 const int maxn=;
 int n,q;
 char ch[]={};
 int val[maxn]={},rig[maxn]={},b[maxn]={},op[maxn][]={};
 int e[maxn][]={},fa[maxn]={},cnt=,sum[maxn]={},tail=;
 int a[maxn]={};
 int xl[maxn*]={},xr[maxn*]={};
 int mx[maxn*]={},ad[maxn*]={};
 int id1,id2,v,zong=;
 int getfa(int x){
     return x==fa[x]?x:getfa(fa[x]);
 }
 inline void downdata(int x,int l,int r){
     if(l!=r){
         mx[lc]+=ad[x];mx[rc]+=ad[x];
         ad[lc]+=ad[x];ad[rc]+=ad[x];
     }
     ad[x]=;
 }
 inline void updata(int x,int l,int r){
     if(l!=r)mx[x]=max(mx[lc],mx[rc]);
 }
 void build(int x,int l,int r){
     if(l==r){mx[x]=a[l];return;}
     downdata(x,l,r);
     int mid=(l+r)/;
     build(lc,l,mid);
     build(rc,mid+,r);
     updata(x,l,r);
 }
 void addit(int x,int l,int r){
     if(id1<=l&&r<=id2){ad[x]+=v;mx[x]+=v;return;}
     int mid=(l+r)/;
     downdata(x,l,r);
     if(id1<=mid)addit(lc,l,mid);
     if(id2>mid)addit(rc,mid+,r);
     updata(x,l,r);
 }
 int getmx(int x,int l,int r){
     if(id1<=l&&r<=id2){return mx[x];}
     int mid=(l+r)/,mm=maxn*(-);
     downdata(x,l,r);
     if(id1<=mid)mm=max(getmx(lc,l,mid),mm);
     if(id2>mid)mm=max(getmx(rc,mid+,r),mm);
     updata(x,l,r);
     return mm;
 }
 int main(){
     scanf("%d",&n);
     for(int i=;i<=n;i++){scanf("%d",&val[i]);fa[i]=i;sum[i]=;}
     scanf("%d",&q);
     int x,y,xx,yy;
     for(int i=;i<=q;i++){
         scanf("%s",ch);
         if(ch[]=='U'){
             op[i][]=;
             scanf("%d%d",&x,&y);op[i][]=x;op[i][]=y;
             xx=getfa(x);yy=getfa(y);
             if(xx==yy)continue;
             if(xx>yy)swap(xx,yy);
             fa[yy]=xx;e[++cnt][]=xx;e[cnt][]=yy;sum[xx]+=sum[yy];
         }
         else if(ch[]=='A'){
             scanf("%d",&op[i][]);
             if(ch[]==''){op[i][]=;scanf("%d",&op[i][]);}
             else if(ch[]==''){op[i][]=;scanf("%d",&op[i][]);}
             else op[i][]=;
         }
         else{
             if(ch[]==''){op[i][]=;scanf("%d",&op[i][]);}
             else if(ch[]==''){op[i][]=;scanf("%d",&op[i][]);}
             else op[i][]=;
         }
     }
     for(int i=;i<=n;i++){
         if(fa[i]==i){
             b[i]=tail+;tail+=sum[i];rig[i]=tail;
             a[b[i]]=val[i];
         }
     }
     for(int i=cnt;i>;i--){
         b[e[i][]]=rig[e[i][]]-sum[e[i][]]+;
         rig[e[i][]]=rig[e[i][]];rig[e[i][]]=b[e[i][]]-;
         a[b[e[i][]]]=val[e[i][]];
     }
     for(int i=;i<=n;i++){fa[i]=i;xl[i]=xr[i]=i;/*cout<<i<<b[i]<<endl;*/}
     build(,,n);
     for(int i=;i<=q;i++){
         if(op[i][]==){
             xx=getfa(b[op[i][]]);yy=getfa(b[op[i][]]);
             if(xx>yy)swap(xx,yy);
             xr[xx]=xr[yy];fa[yy]=xx;
         }
         else if(op[i][]==){id1=b[op[i][]];id2=id1;v=op[i][];addit(,,n);}
         else if(op[i][]==){
             xx=getfa(b[op[i][]]);
             id1=xl[xx];id2=xr[xx];v=op[i][];
             addit(,,n);
         }
         else if(op[i][]==){
             zong+=op[i][];
         }
         else if(op[i][]==){
             id1=b[op[i][]];id2=id1;
             printf("%d\n",getmx(,,n)+zong);
         }
         else if(op[i][]==){
             xx=getfa(b[op[i][]]);id1=xl[xx];id2=xr[xx];
             printf("%d\n",getmx(,,n)+zong);
         }
         else{
             printf("%d\n",mx[]+zong);
         }//id1=1;id2=2;
         //cout<<getmx(1,1,n)<<' '<<1<<endl;
     }
     return ;
 }

离线+线段树