20162325 金立清 S2 W10 C19

20162325 2017-2018-2 《程序设计与数据结构》第10周学习总结

认识

---

• 线性表和树两类数据结构，线性表中的元素是“一对一”的关系，树中的元素是“一对多”的关系，本章所述的图结构中的元素则是“多对多”的关系。图（Graph）是一种复杂的非线性结构，在图结构中，每个元素都可以有零个或多个前驱，也可以有零个或多个后继，也就是说，元素之间的关系是任意的。

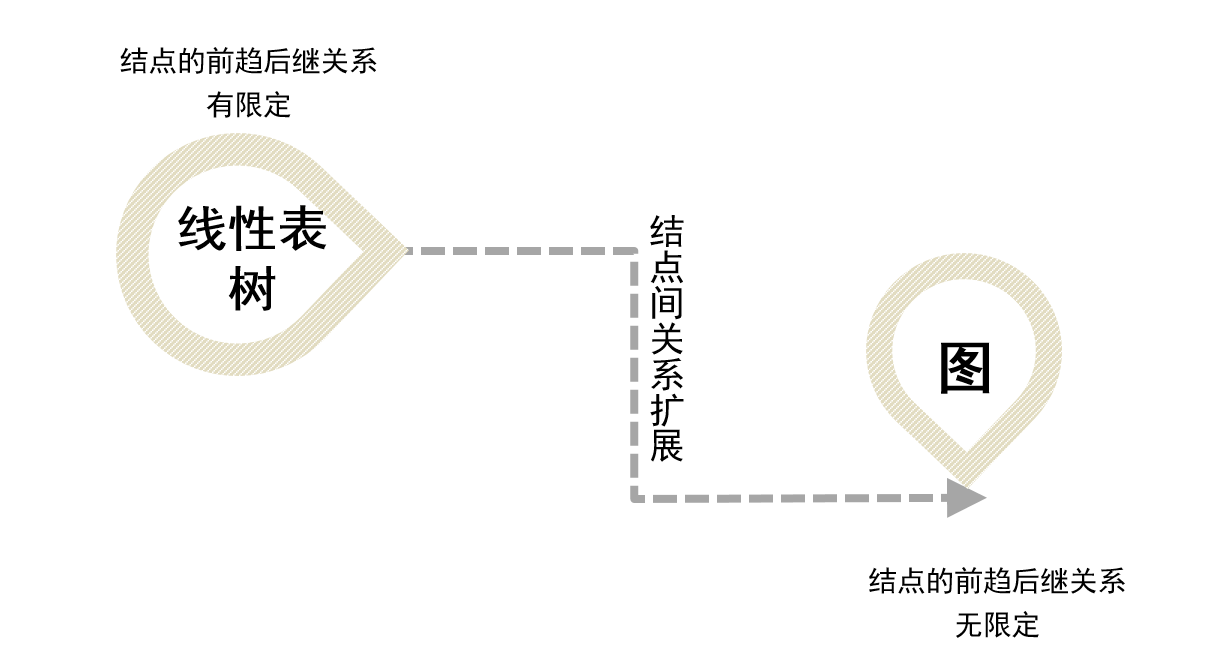
图的基本概念

---

1. 图的定义

定义：图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的；其中，点通常被成为"顶点(vertex)"，而点与点之间的连线则被成为"边或弧"(edege)。

2. 图的种类

根据边是否有方向，将图可以划分为：无向图和有向图。

2.1 无向图

2.2 有向图

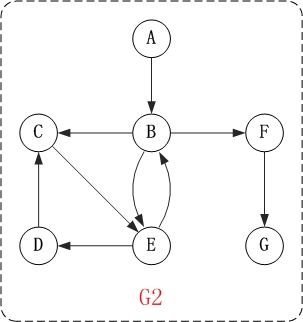
3. 邻接点和度

3.1 邻接点

• 一条边上的两个顶点叫做邻接点。
• 例如，上面无向图G0中的顶点A和顶点C就是邻接点。

有向图：如果<u, v>∈ E, 则称v为u的邻接点，u为v的逆邻接点。边<u, v>与顶点u和v相关联，从u出发的边称为u的出边或邻接边，而指向顶点u的边称为u的入边或逆邻接边。
无向图：如果(u, v)∈ E, 则称u与v互为邻接点。

3.2 顶点的度、入度与出度

• 在无向图中，某个顶点的度是邻接到该顶点的边(或弧)的数目，出度入度相等。
• 例如，上面无向图G0中顶点A的度是2。

在有向图中，顶点v的 入度： 指以顶点为终点的边的数目。 出度：指以顶点起始点的边的数目； 顶点的度=入度+出度。 例如，上面有向图G2中，顶点B的入度是2，出度是3；顶点B的度=2+3=5。

4. 路径和回路

路径：如果顶点(Vm)到顶点(Vn)之间存在一个顶点序列。则表示Vm到Vn是一条路径。
路径长度：路径中"边或弧的数量"。
简单路径：若一条路径上顶点不重复出现，则是简单路径。
回路：若路径的第一个顶点和最后一个顶点相同，则是回路。
简单回路：第一个顶点和最后一个顶点相同，其它各顶点都不重复的回路则是简单回路。

5. 连通图和连通分量

• 连通图：无向图中，若一个顶点到另一个顶点有路径，则称这两个顶点是连通的。如果图中任意两个顶点都是连通的，则称该图是连通图。 有向的连通图称为强连通图。
  

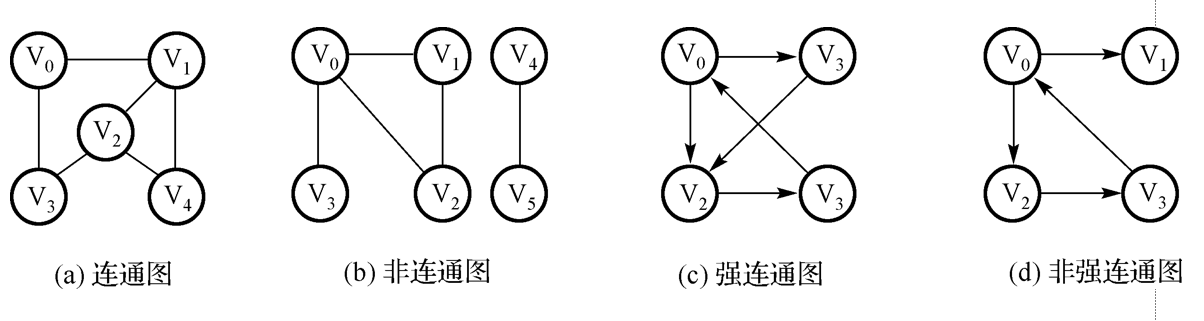
• 连通分量：非连通图中的各个连通子图称为该图的连通分量。

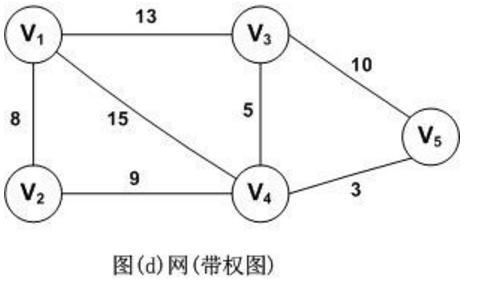
6. 权

• 图的边和弧上相关的数，叫做权（Weight）。这些带权的图通常称为网（Network）。
  

图的存储结构

---

　　

• 图的结构比价复杂，任意两个顶点之间都可能存在关系，不能用简单的顺序存储结构来表示。如果运用多重链表，即一个数据域多个指针域组成的结点表示图中一个结点，则造成大量存储单元浪费。图的存储结构，常用的是"邻接矩阵"和"邻接表"，此外还有"十字链表"。

1. 邻接矩阵

• 邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。
  假设图中顶点数为n，则邻接矩阵定义为：
  

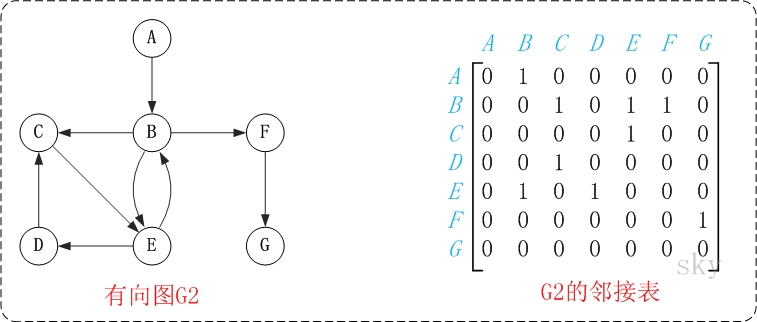
• 通常采用两个数组来实现邻接矩阵：一个一维数组用来保存顶点信息，一个二维数组来用保存边的信息。

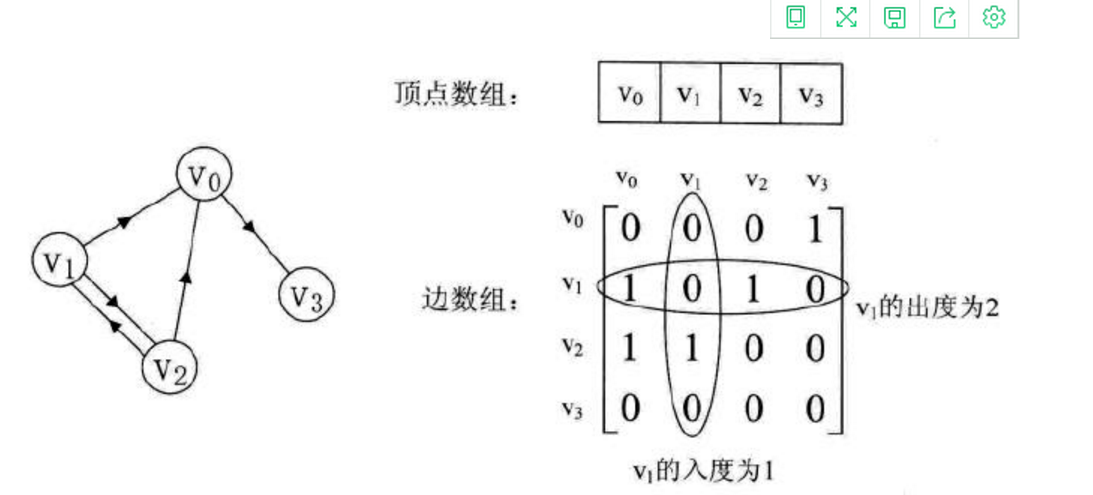
• 邻接矩阵具有以下特点：

a)邻接矩阵是正矩阵，即横纵维数相等。
b)矩阵的每一行或一列代表一个顶点，行与列的交点对应这两个顶点的边。
c)矩阵的点代表边的属性，1代表有边，0代表无边，所以矩阵的对角线都是0，因为对角线上对应的横纵轴代表相同的顶点，边没有意义。
d)如果是无向图，那么矩阵是对称矩阵，也一定是对称矩阵（主对角线（左上到右下）相等）；如果是有向图则不一定。
e)如果是有权图，矩阵点数值可以是权值。
f)邻接矩阵表示图的关系非常清晰，但消耗空间较大。

2. 邻接表

• 对于边相对与定点较少的图，邻接矩阵表示很浪费空间
  

• 邻接表是图的一种链式存储表示方法，以一组链表来表示顶点间关系，它是改进后的"邻接矩阵"。

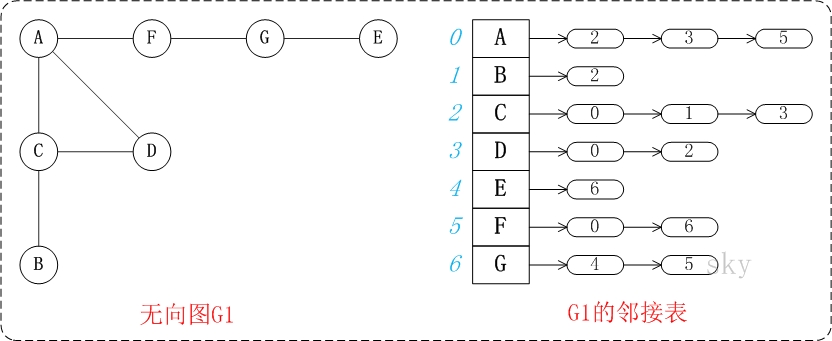
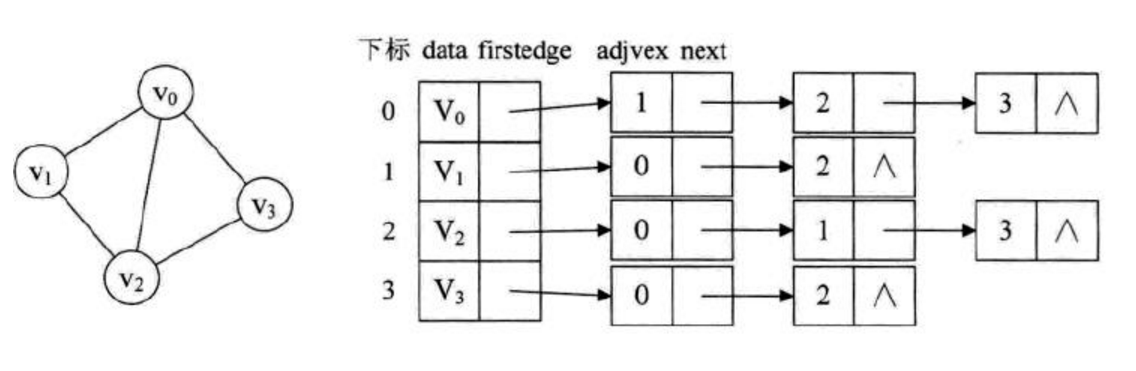
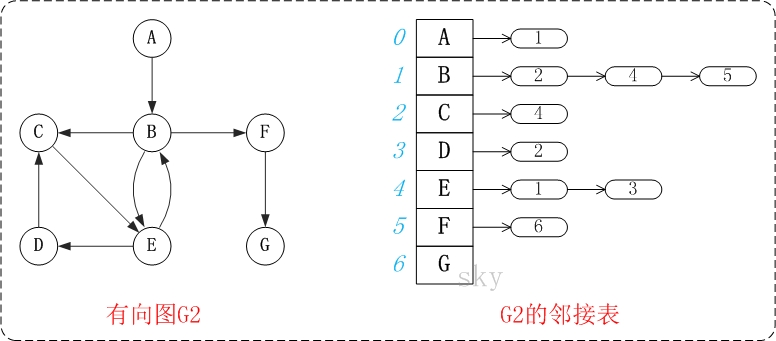
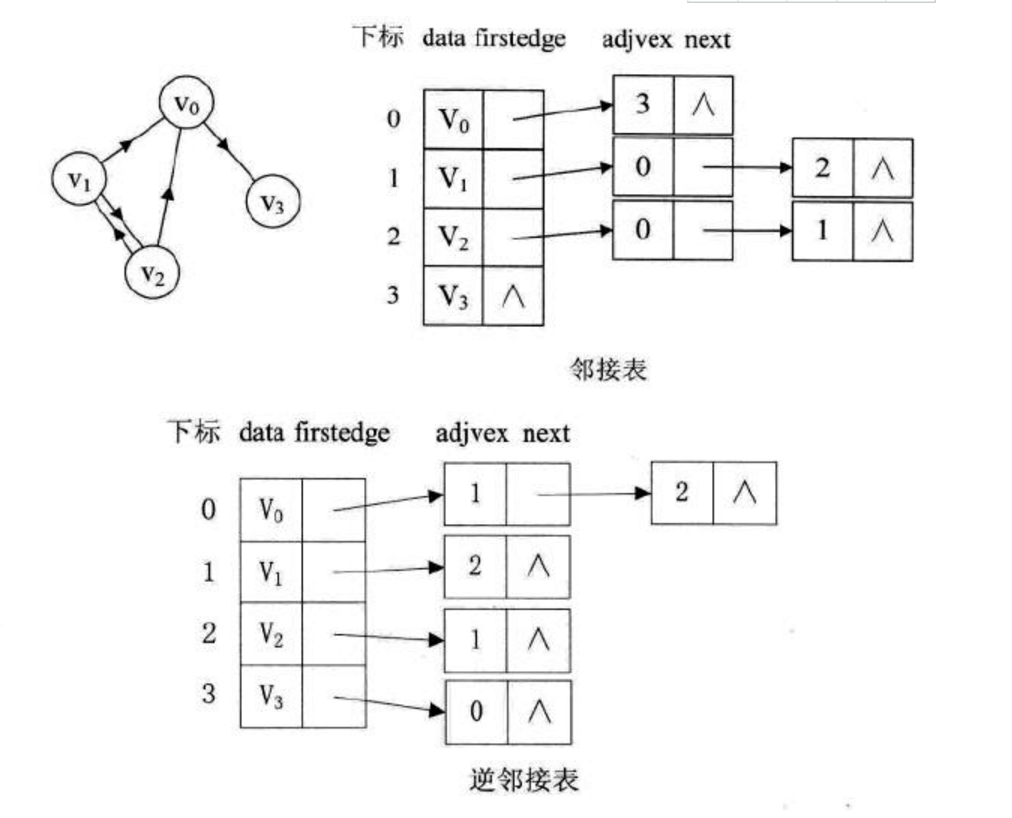
• 一个有向图的逆邻接表，就是对每个顶点vi都建议一个链接为vi为弧头的表。

• 邻接表具有以下特点：

a)邻接表示一个有但链表组成的数组。
b)图中的每一个顶点都有一个链，数组的大小等于图中顶点的个数。
c)无向图的链的第一个元素是本顶点，后继分别连接着和这个顶点相连的顶点；有向图的链第一个顶点是本顶点，后继是以本顶点为起点的边的终点。
如果是有权图，可以在节点元素中设置权值属性。
d)邻接链表关系表示不如邻接矩阵清晰，不方便判断两个顶点之间是否有边，但节省空间。

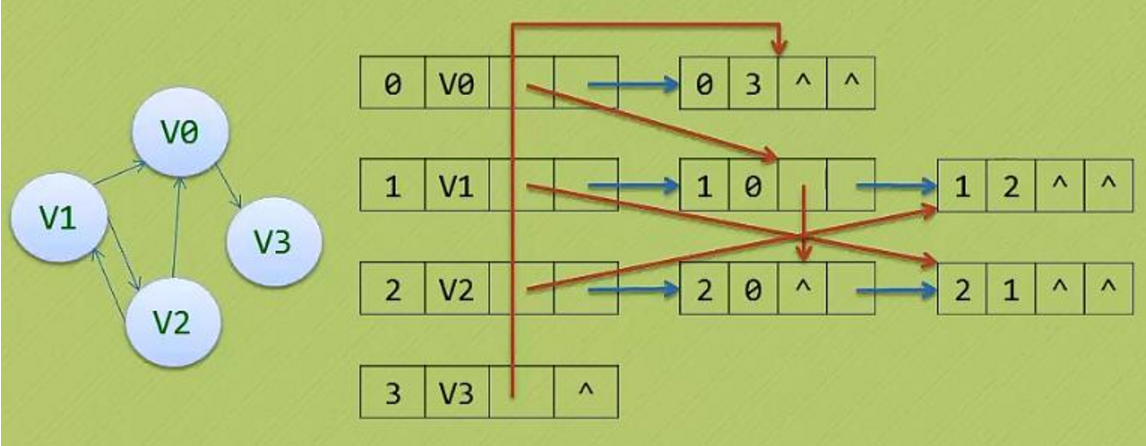
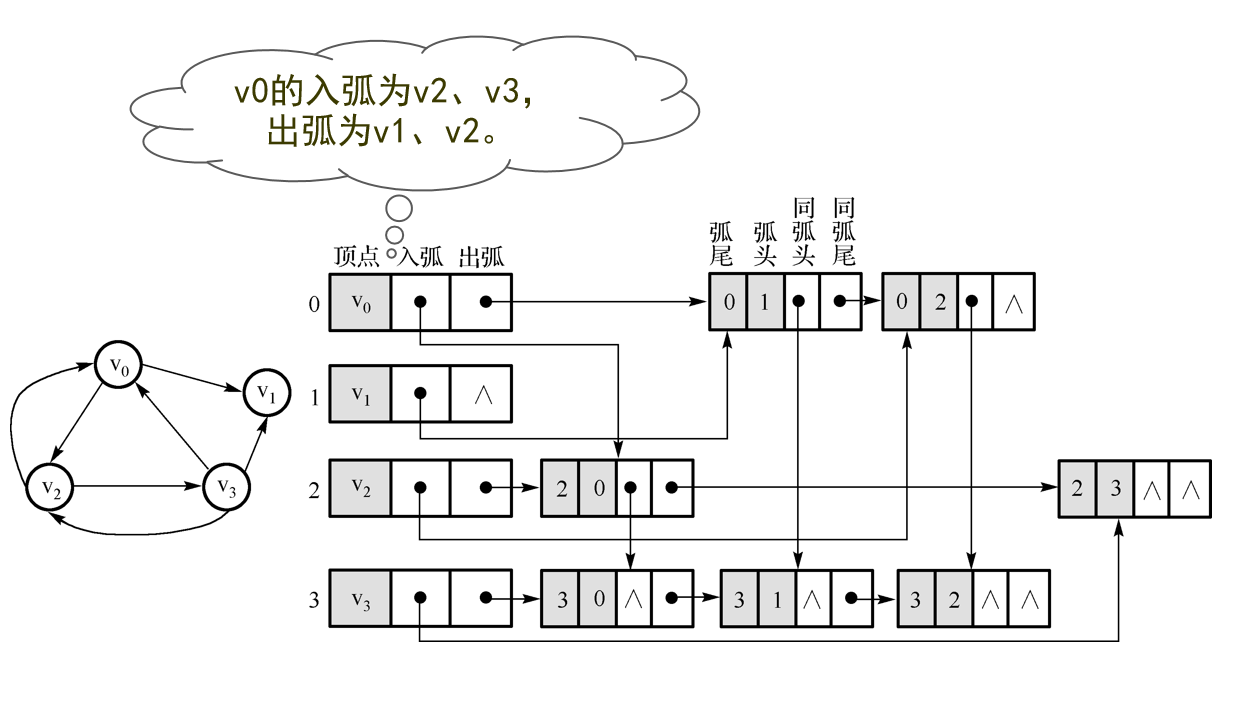
十字链表

• 顶点表结点结构：
  

　　firstin：表示入边表头指针，指向该顶点的入边表中第一个结点。

　　firstout：表示出边表头指针，指向该顶点的出边表中的第一个结点。

• 边表结点结构：
  

　　tailvex：指弧起点在顶点表的下标。

　　headvex：指弧终点在顶点表中的下标。

　　headlink：指入边表指针域。

　　taillink：指边表指针域。

• 如果是网，还可以再增加一个weight域来存储权值。
  

图的遍历

---

1) 深度优先搜索遍历（栈）

深度优先搜索DFS遍历类似于树的前序遍历。其基本思路是：

a) 假设初始状态是图中所有顶点都未曾访问过，则可从图G中任意一顶点v为初始出发点，首先访问出发点v，并将其标记为已访问过。

b) 然后依次从v出发搜索v的每个邻接点w，若w未曾访问过，则以w作为新的出发点出发，继续进行深度优先遍历，直到图中所有和v有路径相通的顶点都被访问到。

c) 若此时图中仍有顶点未被访问，则另选一个未曾访问的顶点作为起点，重复上述步骤，直到图中所有顶点都被访问到为止。

图示如下：

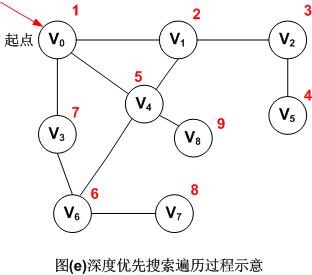
注：红色数字代表遍历的先后顺序，所以图(e)无向图的深度优先遍历的顶点访问序列为：V0，V1，V2，V5，V4，V6，V3，V7，V8

如果采用邻接矩阵存储，则时间复杂度为O(n2)；当采用邻接表时时间复杂度为O(n+e)。

2) 广度优先搜索遍历（队列）

广度优先搜索遍历BFS类似于树的按层次遍历。其基本思路是：

a) 首先访问出发点Vi

b) 接着依次访问Vi的所有未被访问过的邻接点Vi1，Vi2，Vi3，…，Vit并均标记为已访问过。

c) 然后再按照Vi1，Vi2，… ，Vit的次序，访问每一个顶点的所有未曾访问过的顶点并均标记为已访问过，依此类推，直到图中所有和初始出发点Vi有路径相通的顶点都被访问过为止。

图示如下：

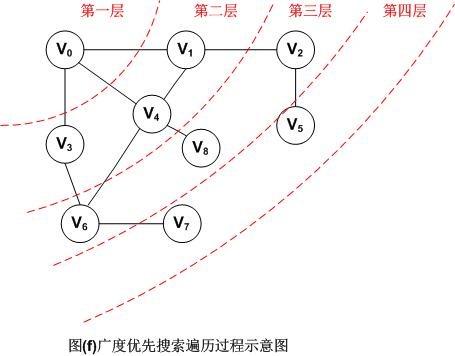
因此，图(f)采用广义优先搜索遍历以V0为出发点的顶点序列为：V0，V1，V3，V4，V2，V6，V8，V5，V7

如果采用邻接矩阵存储，则时间复杂度为O(n2)，若采用邻接表，则时间复杂度为O(n+e)。

最小生成树和最短路径

---

1，最小生成树

在弄清什么是最小生成树之前，我们需要弄清什么是生成树？

用一句语简单概括生成树就是：生成树是将图中所有顶点以最少的边连通的子图。

比如图(g)可以同时得到两个生成树图(h)和图(i)

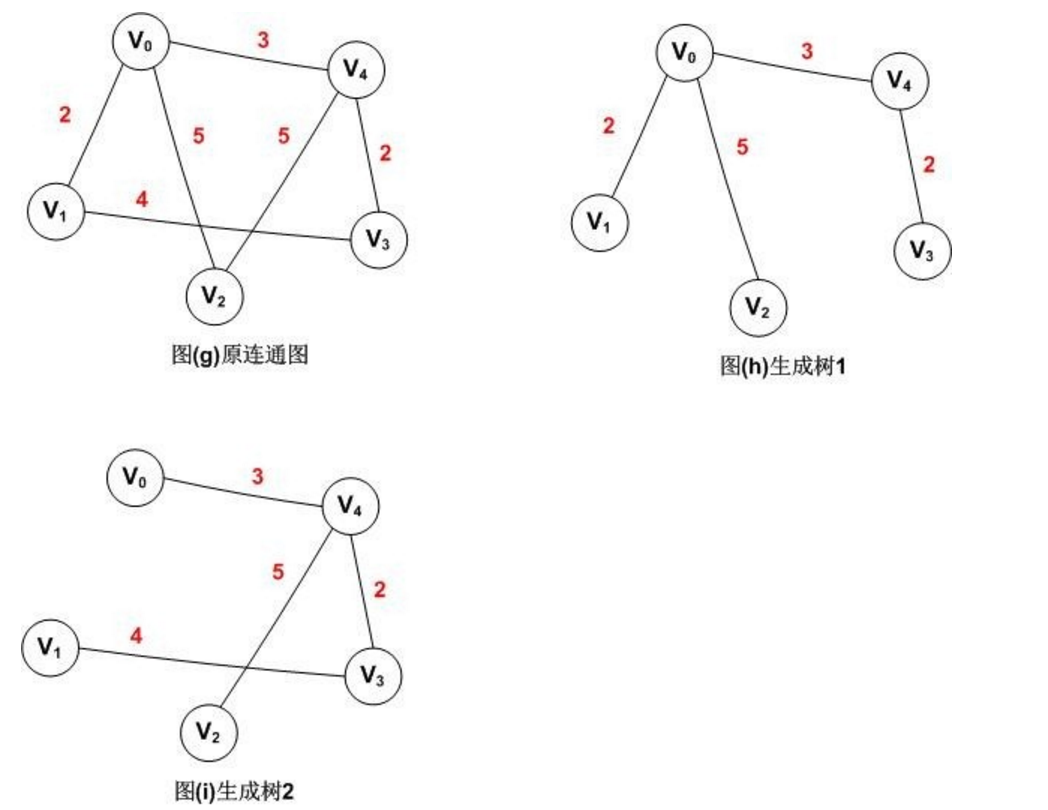
那所谓最小生成树，用一句话总结就是：权值和最小的生成树就是最小生成树。

比如上图中的两个生成树，生成树1和生成树2，生成树1的权值和为：12，生成树2的权值为：14，我们可以证明图(h)生成树1就是图(g)的最小生成树。

如何构造最小生成树呢？可以使用普里姆算法——参见数据结构与算法--图 - CSDN博客

2，最短路径

求最短路径也就是求最短路径长度。下面是一个带权值的有向图，表格中分别列出了顶点V1其它各顶点的最短路径长度。

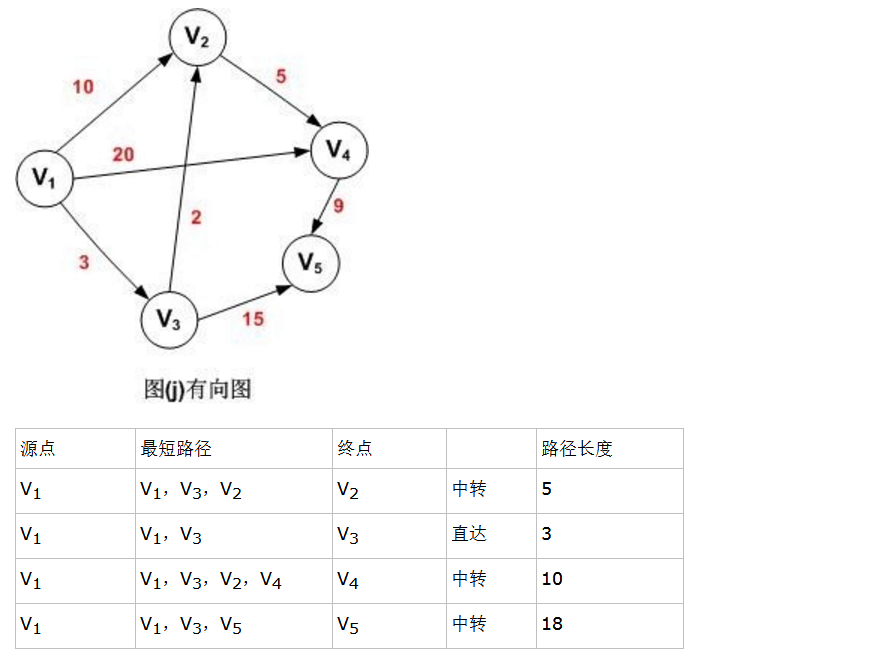
表：顶点V1到其它各顶点的最短路径表

从图中可以看出，顶点V1到V4的路径有3条(V1，V2，V4)，(V1，V4)，(V1，V3，V2，V4)，其路径长度分别为15，20和10，因此，V1到V4的最短路径为(V1，V3，V2，V4)。

如何求带权有向图的最短路径长度呢？可以使用迪杰斯特拉算法——同样参见数据结构与算法--图 - CSDN博客

教材学习中的问题和解决过程

---

• 问题1：书上P423页说道“用邻接矩阵表示带权图，用矩阵中的每个位置表示边的权就可以”，不明白是怎么表示的。

• 问题1解决方案：上网查找答案，参考java 图的邻接矩阵

• 问题2：邻接矩阵与邻接表的比较？

• 问题2解决方案：
  当图中结点数目较小且边较多时，采用邻接矩阵效率更高。
  当节点数目远大且边的数目远小于相同结点的完全图的边数时，采用邻接表存储结构更有效率。

代码调试中的问题和解决过程

---

• 这周主要代码在实验部分，请见实验博客

代码托管

---

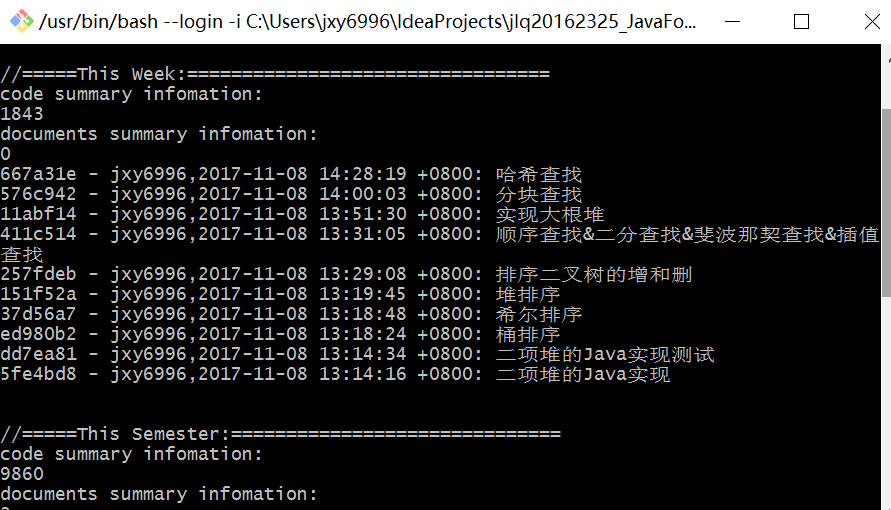
上周考试错题总结

---

• 
  

• 解答：解析和答案相符，可能是系统出错？

-

• 解答：

• 

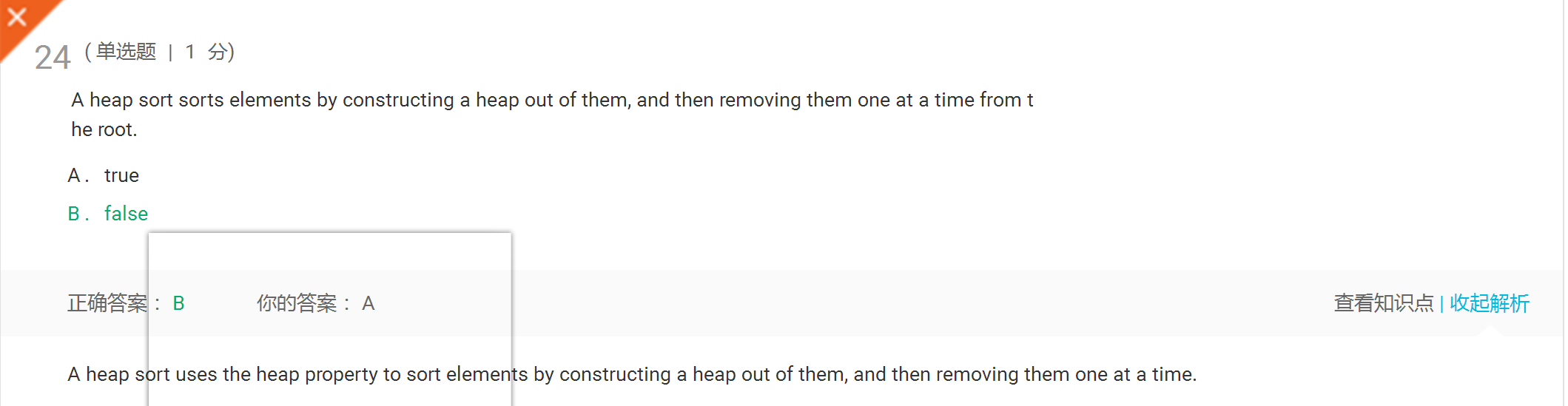
• 解答：是删除堆，不是从根目录

本周结对学习情况

---

• 结对搭档
  • 20162311
• 结对学习内容
  • 蓝墨测试题

其他（感悟、思考等，可选）

---

• 这周的主要任务是实验三，小部分实验内容是以前做过的，更多是在之前的基础上结合后面学到的知识加以拓展应用。这学期的团队项目快要正式拉开帷幕了，还是有一点紧张，但相信在和队友的通力合作下，我们组的成果会令人满意的！

学习进度条

---

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	58/	1/1	10/10
第二周			8/18
第三周	134/	3/4	12/ 30
第四周		2/6	12/42
第五&六周	750/ 6595	5/11	24/66
第七周	764/7068	7/13	18/84
第八周	888/7956	9/15	20/104
第九周	475/8431	12/18	22/126
第十周	1429/9860	16/22	24/150

• 计划学习时间: 24小时

• 实际学习时间: 24小时

• 改进情况：只是想吐槽一下……每周要写的博客真多

参考资料

---

• 图的理论基础 - 如果天空不死 - 博客园
• 浅析数据结构-图的基本概念 - bldong - 博客园
• 数据结构——图（1），图的存储结构Java实现 - CSDN博客
• java 数据结构 图 - snail-lb - 博客园
• 数据结构和算法系列17 图 - 永远的麦子 - 博客园
• 数据结构与算法--图 - CSDN博客