【模式匹配】KMP算法的来龙去脉

1. 引言

字符串匹配是极为常见的一种模式匹配。简单地说，就是判断主串\(T\)中是否出现该模式串\(P\)，即\(P\)为\(T\)的子串。特别地，定义主串为\(T[0 \dots n-1]\)，模式串为\(P[0 \dots p-1]\)，则主串与模式串的长度各为\(n\)与\(p\)。

暴力匹配

暴力匹配方法的思想非常朴素：

1. 依次从主串的首字符开始，与模式串逐一进行匹配；
2. 遇到失配时，则移到主串的第二个字符，将其与模式串首字符比较，逐一进行匹配；
3. 重复上述步骤，直至能匹配上，或剩下主串的长度不足以进行匹配。

下图给出了暴力匹配的例子，主串T="ababcabcacbab"，模式串P="abcac"，第一次匹配：

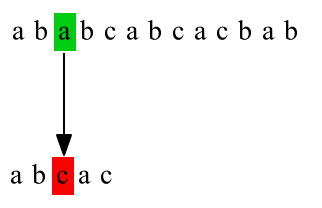
第二次匹配：

第三次匹配：

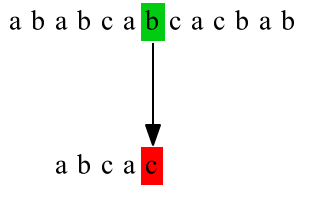
C代码实现：

int brute_force_match(char *t, char *p) {
    int i, j, tem;
    int tlen = strlen(t), plen = strlen(p);
    for(i = 0, j = 0; i <= tlen - plen; i++, j = 0) {
        tem = i;
        while(t[tem] == p[j] & j < plen) {
            tem++;
            j++;
        }
        // matched
        if(j == plen) {
            return i;
        }
    }
    // [p] is not a substring of [t]
    return -1;
}

时间复杂度：i在主串移动次数（外层的for循环）有\(n-p\)次，在失配时j移动次数最多有\(p-1\)次（最坏情况下）；因此，复杂度为\(O(n*p)\)。

---

我们仔细观察暴力匹配方法，发现：失配后下一次匹配，

• 主串的起始位置 = 上一轮匹配的起始位置 + 1；
• 模式串的起始位置 = 首字符P[0]。

如此未能利用已经匹配上的字符的信息，造成了重复匹配。举个例子，比如：第一次匹配失败时，主串、模式串失配位置的字符分别为 a 与 c，下一次匹配时主串、模式串的起始位置分别为T[1]与P[0]；而在模式串中c之前是ab，未有重复字符结构，因此T[1]与P[0]肯定不能匹配上，这样造成了重复匹配。直观上，下一次的匹配应从T[2]与P[0]开始。

2. KMP算法

KMP思想

根据暴力方法的缺点，而引出KMP算法的思想。首先，一般化匹配失败，如下图所示：

在暴力匹配方法中，下一次匹配开始时，主串指针会回溯到i+1，模式串指针会回退到0。那么，如果不让主串指针发生回溯，模式串的指针应回退到哪个位置才能保证正确匹配呢？首先，我们从上图中可以得到已匹配上的字符：

\[T[i \dots i+j-1] = P[0 \dots j-1]
\]

KMP算法思想便是利用已经匹配上的字符信息，使得模式串的指针回退的字符位置能将主串与模式串已经匹配上的字符结构重新对齐。当有重复字符结构时，下一次匹配如下图所示：

从图中可以看出，下一次匹配开始时，主串指针在失配位置i+j，模式串指针回退到m+1；模式串的重复字符结构：

\begin{equation}

T[i+j-m-1 \dots i+j-1] = P[j-m-1 \dots j-1] = P[0 \dots m]

\label{eq:overlap}

\end{equation}

且有

\[T[i+j] \neq P[j] \neq P[m+1]
\]

那么应如何选取\(m\)值呢？假定有满足式子\eqref{eq:overlap}的两个值\(m_1 > m_2\)，如下图所示：

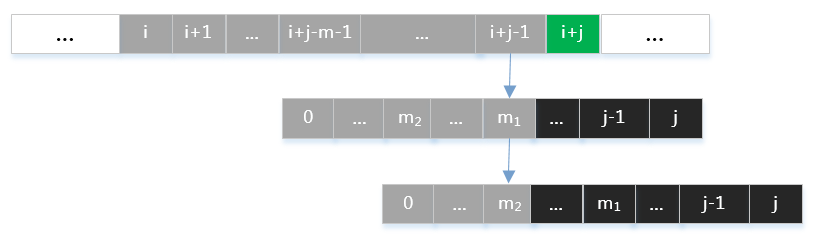
如果选取\(m=m_2\)，则会丢失\(m=m_1\)的这一种字符匹配情况。由数学归纳法容易知道，应取所有满足式子\eqref{eq:overlap}中最大的\(m\)值。

---

KMP算法中每一次的匹配，

• 主串的起始位置 = 上一轮匹配的失配位置；
• 模式串的起始位置 = 重复字符结构的下一位字符（无重复字符结构，则模式串的首字符）

模式串P="abcac"匹配主串T="ababcabcacbab"的KMP过程如下图：

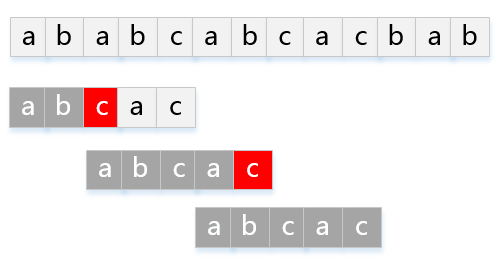
部分匹配函数

根据上面的讨论，我们定义部分匹配函数（Partial Match，在数据结构书[2]称之为失配函数）：

\[f(j) = \left\{ {\matrix{
{\max \{ m \} } & P[0\dots m]=P[{j-m}\dots {j}],0\le m < j \cr
{-1} & else \cr
} } \right.
\]

其表示字符串\(P[0 \dots j]\)的前缀与后缀完全匹配的最大长度，也表示了模式串中重复字符结构信息。KMP中大名鼎鼎的next[j]函数表示对于模式串失配位置j+1，下一轮匹配时模式串的起始位置（即对齐于主串的失配位置）；则

\[next[j] = f(j)+1
\]

如何计算部分匹配函数呢？首先来看一个例子，模式串P="ababababca"的部分匹配函数与next函数如下：

j	0	1	2	3	4	5	6	7	8	9
P[j]	a	b	a	b	a	b	a	b	c	a
f(j)	-1	-1	0	1	2	3	4	5	-1	0
next[j]	0	0	1	2	3	4	5	6	0	1

模式串的f(j)满足\(P[0 \dots f(j)]=P[j-f(j) \dots j]\)，在计算f(j+1)分为两类情况：

• 若\(P[j+1]=P[f(j)+1]\)，则有\(P[0 \dots f(j)+1]=P[j-f(j) \dots j+1]\)，因此f(j+1)=f(j)+1。
• 若\(P[j+1] \neq P[f(j)+1]\)，则要从\(P[0 \dots f(j)]\)中找出满足P[f(j+1)]=P[j+1]的f(j+1)，从而得到\(P[0 \dots f(j+1)]=P[j+1-f(j+1) \dots j+1]\)

其中，根据f(j)的定义有：

\[P[j]=P[f(j)]=P[f(f(j))]=\cdots = P[f^k(j)]
\]

其中，\(f^k(j)=f(f^{k-1}(j))\)。通过上面的例子可知，函数\(f^k(j)\)是随着\(k\)递减的，并最后收敛于-1。此外，P[j]与p[j+1]相邻；因此若存在P[f(j+1)]=P[j+1]，则必有

\[f(j+1)=f^k(j)+1
\]

为了求满足条件的最大的f(j+1)，因\(f^k(j)\)是随着\(k\)递减的，故应为满足上式的最小\(k\)值。

综上，部分匹配函数的计算公式如下：

\[f(j) = \left\{ {\matrix{
{f^k(j-1)+1} & \min \limits_{k} P[f^k(j-1)+1]=P[j] \cr
{-1} & else \cr
} } \right.
\]

代码实现

部分匹配函数（失配函数）的C实现代码：

int *fail(char *p) {
    int len = strlen(p);
    int *f = (int *) malloc(len * sizeof(int));
    f[0] = -1;
    int i, j;
    for(j = 1; j < len; j++) {
        for(i = f[j-1]; ; i = f[i]) {
            if(p[j] == p[i+1]) {
                f[j] = i + 1;
                break;
            }
            else if(i == -1) {
                f[j] = -1;
                break;
            }
        }
    }
    return f;
}

KMP的C实现代码：

int kmp(char *t, char *p) {
    int *f = fail(p);
    int i, j;
    for(i = 0, j = 0; i < strlen(t) && j < strlen(p); ) {
        if(t[i] == p[j]) {
            i++;
            j++;
        }
        else if(j == 0)
            i++;
        else
            j = f[j-1] + 1;
    }
    return j == strlen(p) ? i - strlen(p) : -1;
}

时间复杂度：fail函数的复杂度为\(O(p)\)，kmp函数的复杂度为\(O(n)\)，所以整个KMP算法的复杂度为\(O(n+p)\)。

3. 参考资料

[1] dekai, Lecture 16: String Matching.

[2] E. Horowitz, S. Sahni, S. A. Freed, 《Fundamentals of Data Structures in C》.

[3] Jake Boxer, The Knuth-Morris-Pratt Algorithm in my own words.