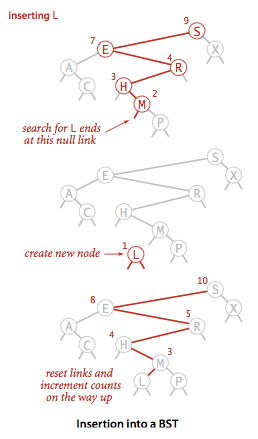
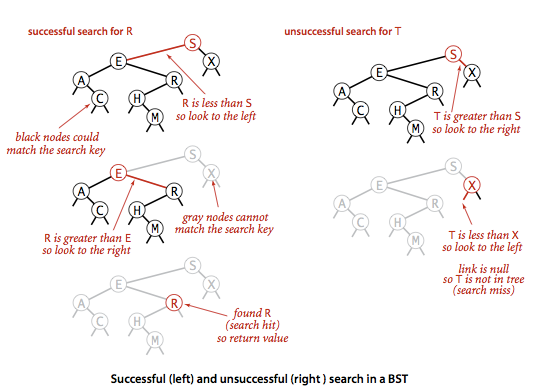
数据结构：JAVA_二叉数查找树基本实现（上）

数据结构：JAVA实现二叉查找树

写在前面

　　二叉查找树（搜索树）是一种能将链表插入的灵活性与有序数组查找的高效性结合在一起的一种数据结构。

　　

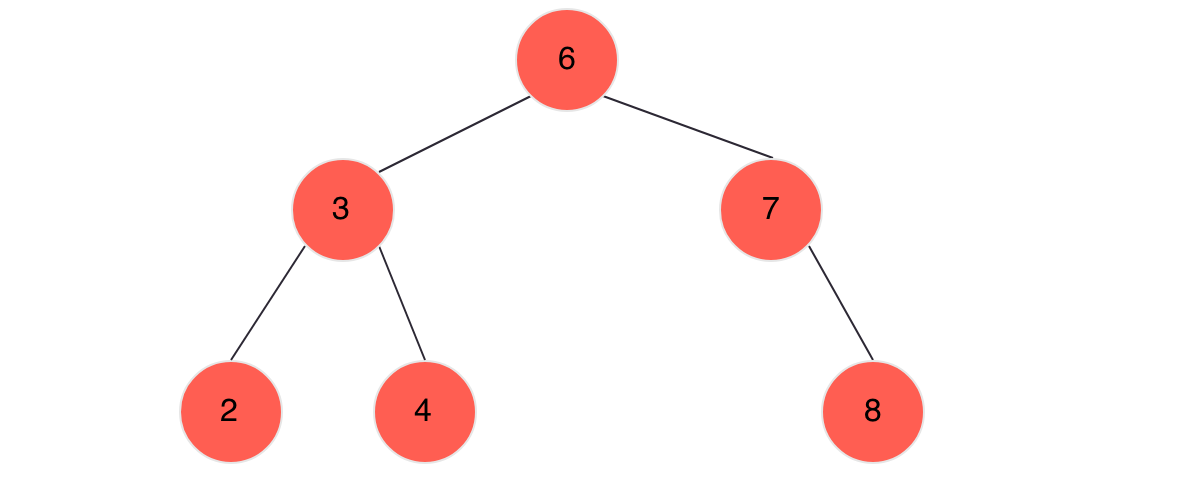
　　观察二叉查找树，我们发现任何一个节点大于左子节点且小于其右子节点，也就是说一个节点的左子树的所有值都小于当前节点，右子树中的所有值都大于当前节点，其中序遍历结果应该是[2,3,4,6,7,8]，这是一组排序值，在一组有序值中找到一个特定值最快的方法是二分搜索，也就是说我们在查找树中查找某个特点值的时候也是在做二路选择，即总会在两条路线中做出选择，一定会舍弃其中一条路线。这是完全等同于我们之前学过的二分搜索的。

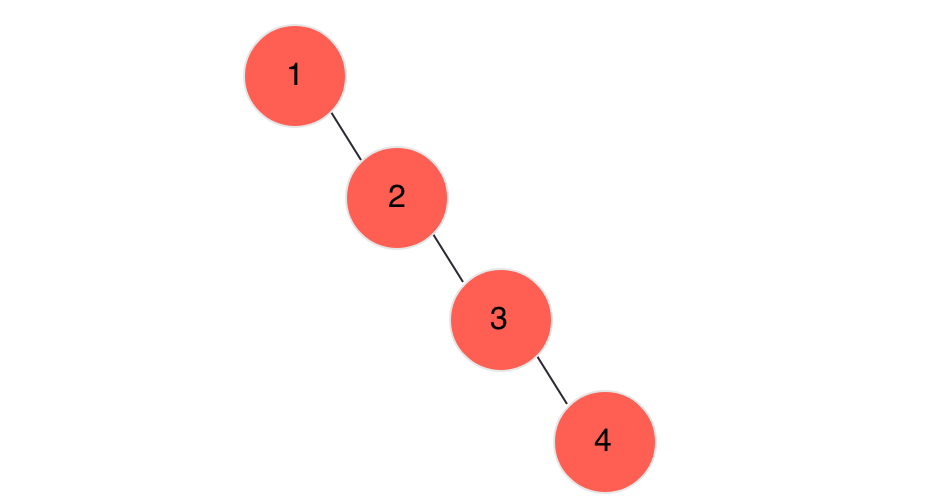
　　搜索、插入、删除的复杂度等于树高，期望O(log n)，最坏O(n)（数列有序，树退化成线性表，如下图所示）。

　　

代码分解

对节点的结构定义

public class BinaryTree <Key extends Comparable<Key>,Value>{
　　.......private class Node {
        private Key key;
        private Value val;
        private Node Left, Right;
        private int N; //以该节点为根的子树中的节点总数
        public Node(Key key,Value val,int N) {
            this.val = val;
            this.key = key;
        }
    }
　　......
}

　　　　

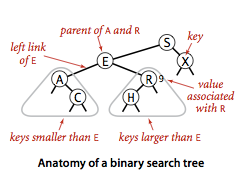
　说明

　　　　1.节点具有什么样的功能呢？首先应该拥有自己的键值，其次能指示左右节点，这是二叉树节点中最基本的内容。

　　　　2.上面的结构中将节点写为内部类，更好的封装了节点，对外提供更加简洁的接口。

插入(排序)操作

   public void put(Key k,Value v)
    {
        root = put(root,k,v);
    } 
 
     public Node put(Node x,Key k,Value v)
    {
        if(x==null) return new Node(k,v,1); //默认设置子树包含的节点个数为1
 
        int cmp = k.compareTo(x.key);
        if(cmp==0)
            x.val=v;
 
        if(cmp<0)
            x.Left=put(x.Left,k,v);
        else
            x.Right=put(x.Right,k,v);
 
        x.N=size(x.Left)+size(x.Right)+1;
        return x;
    }

说明：

　　　　1.插入的流程应该是什么样子的呢？

　　　　

　　　　2.由于二叉树的特殊结构，每次递归都是有意义的，不需要回溯重走等等操作便可以直接走到目标处。以下分析仅仅是一种特例情况。

　　　　3.对递归的简单分析：　　　　

　　　　　　首先从root节点开始，如果root节点不存在，就把root节点初始化为该节点。
                     　　　　如果root节点存在，判断键值与root的关系，如果大于往右边走，如果小于往左边走。 （此处往左边走！！）
                        　　　　如果root.Left节点存在，判断键值与root.Left的关系，如果大于往右边走，如果小于往左边走  （此处往左边走！！）
                           　　　　 如果root.left.left节点存在，判断键值与root.Left.Left的关系，如果大于往右边走，如果小于往左边走  
                          　　 　　 ....
                               　　　　 如果root....left不存在，建立节点。
                               　　　　 ..
                              　　　　  如果root....left节点存在，且键值存在相等则修改，并统计N，即子树中节点个数。

查找操作

public Value get(Key k)
    {
        return get(root,k);
    }
    public Value get(Node x,Key k)
    {
        if(x==null) return null;
        int cmp = k.compareTo(x.key);
        if(cmp==0)
            return x.val;
        if(cmp<0)
            return get(x.Left,k);
        else
            return get(x.Right,k);
    }

说明：

　　　　1.获取的流程是怎样的呢？其实就是插入的简化版咯。

　　　　　　

　　　　　　2.同样，由于二叉树的特殊性，我认为不存在无用递归，路径是直通目标节点的。

    　　　　  3.关于这里的递归，return方法并不是意味着要返回多个，每一次的return后面的语句都是在递归，所以直到返回目标节点。

 

关于Size方法和测试方法

public int size(Node X) //返回该节点的子树中的节点个数
{
    if(X==null) return 0;
    else return X.N;
}