GDUFE-OJ 1359校庆素数 埃氏筛法

Problem Description:

包含33的素数称为校庆素数。
她想知道在L和R之间（包含L和R）有多少个校庆素数。
比如 2333 就是一个校庆素数。

Input:

输入的第一行包括一个T(T <= 50)，代表有T组数据。
每组数据输入两个整数L和R (1<= L <= R <= 500000)。

Output:

对于每组数据，输出"Case #x: y"（不包括引号），其中x代表数据的编号，从1开始，y代表该组数据的结果。

Sample Input:

2
1 233
1 232

Sample Output:

Case #1: 1
Case #2: 0

Hints:
1到233中只有233是校庆素数。

 思路：先将1-500000的所有素数筛出，并在此过程中筛出含‘33’的数，最后在L到R之间计数。

 #include <stdio.h>
 #include <string.h>
 ],ch33[],k=;

 int is33(int l)//筛出包含‘33’的数
 {
     )
     {
         ==);
         l/=;
     }
     ;
 }

 void judge()//判断素数（埃氏筛法）
 {
     long long  i,j;
 memset(ch,-,sizeof(ch));//将ch所有元素初始化为-1
     ;i<=;i++)
         )
         {
             if(is33(i))
                 {
                     ch33[k++]=i;//存入ch33数组
                 }
         ;j+=i)
             ch[j]=;
         }
 }

 int main()
 {
     ,g,a,L,R,i;
     judge();
     while(scanf("%d",&n)!=EOF)
     while(n--)
     {
         s++;
         scanf("%d%d",&L,&R);
         ,a=;g<k;g++)
         {
                 if(ch33[g]>=L&&ch33[g]<=R)a++;
                 if(ch33[g]>R)break;
         }
         printf("Case #%d: %d\n",s,a);
     }
     ;
 }

以下是埃氏筛法的示意图：

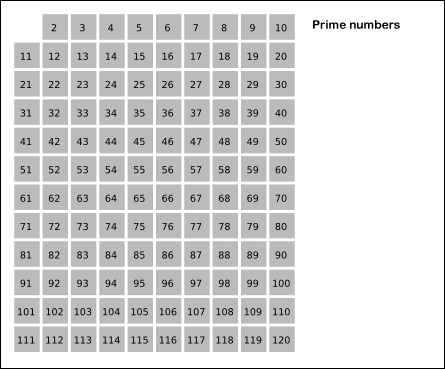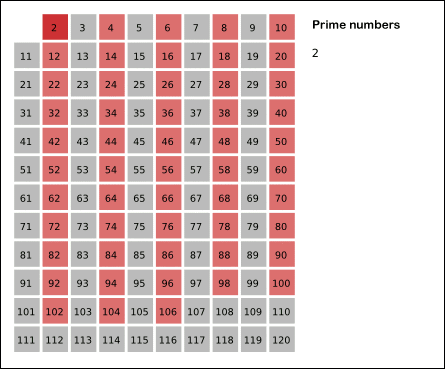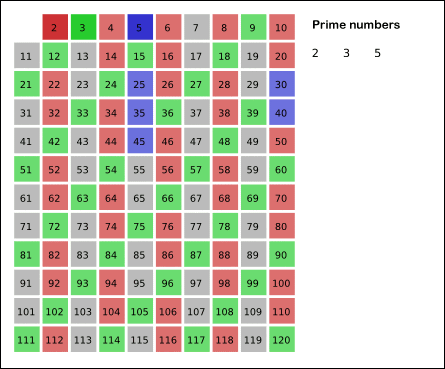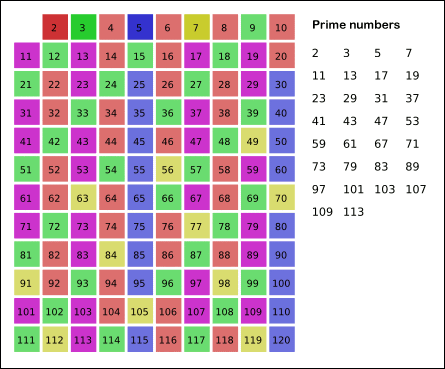
原理：

1.  根据算术基本定理（百度）：任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积。

2.  先用2筛，筛走不是素数的数（也就是2的倍数），接着用3,5,7……直到最后一位。

3.  被筛走的可以标记，后面就不再用这个数筛。

Tips：

1.sizeof是判断数据类型或者表达式长度符，用于计算有多少个字节。

sizeof(int)==4。

char ch[10]="abc",sizeof(ch)==10*1。

2.strlen是求字符串（仅字符串）长度的函数。char ch[10]="abc",strlen(ch)==3.

3.memset

void *memset(void *s, int ch, sizeof(n));

解释：将s中当前位置后面的n个字节 (typedef unsigned int size_t)用 ch 替换并返回 s 。

对数组操作时只能用于数组的置0或-1，其他值无效。

memset(ch,-1,sizeof(ch))就是将数组ch中所有元素替换为-1，返回ch。