Educational Codeforces Round 57 (Rated for Div. 2)

我好菜啊。

A - Find Divisible

好像没什么可说的。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<cmath>
#include<cctype>
using namespace std;

typedef long long ll;
const int Maxn=110000;

int t,l,r;

int main() {
	scanf("%d",&t);
	while(t--) {
		scanf("%d%d",&l,&r);
		printf("%d %d\n",l,l<<1);
	}
	return 0;
}

B - Substring Removal

如果所有的字符都是一样的，那就直接输出n*(n+1)/2。

如果开始的x个字符相同，最后的y个字符相同，那么如果第一个字符和最后一个字符相同，那么答案就是(x+1)*(y+1)，否则就是x+y+1。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<cmath>
#include<cctype>
using namespace std;

typedef long long ll;
const int Maxn=210000;

int n;
char s[Maxn];

int main() {
	scanf("%d",&n);
	scanf("%s",s);
	int flag=0;
	for(int i=1;i<n;i++) if(s[i]!=s[i-1]) {
		flag=1;
		break;
	}
	if(flag) {
		int temp=2,tempp=2;
		for(int i=1;i<n;i++) if(s[i]==s[i-1]) temp++;
		else break;
		for(int i=n-2;i>=0;i--) if(s[i]==s[i+1]) tempp++;
		else break;
		if(s[0]==s[n-1]) printf("%I64d\n",1ll*temp*tempp%998244353);
		else printf("%d\n",temp+tempp-1);
	}
	else printf("%I64d",1ll*n*(n+1)/2%998244353);
	return 0;
}

C - Polygon for the Angle

C的规律好难找啊。好像别人都是打表？那我来讲一下我是怎么证的吧。

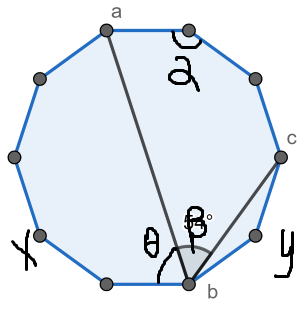
首先如图所示，正n边形的一个内角的度数为\(\alpha=\frac{(n-2)\cdot 180}{n}\)，而要求的角为\(\beta\)。

从b点到a点要走x条边，那么ab这条线左边构成了一个x+1边形，其内角和为\((x-1)\cdot 180\)，其中又有x-1个度数为\(\alpha\)的角，而剩下的两个角相等，那么\(\theta=\frac{(x-1)(180-\alpha)}{2}\)，右边的角同理，所以\(\beta=\alpha-\frac{(x+y-2)\cdot (180-\alpha)}{2}\)，化简并带入\(\alpha\)可得\(n\beta=(n-x-y)\cdot 180\)，因为\(1\le x,y\ and\ x+y<n\)，那么设\(d=n-x-y,1\le d\le n-2\)，那么我们令n为180，则d为\(\beta\)，然后化简公约数后如果d等于n-1，那么让两个数同乘2即可，最后输出n。大概这样最大的优点就是可以做分数的情况，而打表是打不了的。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<cmath>
#include<cctype>
using namespace std;

typedef long long ll;
const int Maxn=210000;

int gcd(int a,int b) {
	return b?gcd(b,a%b):a;
}

int main() {
	int t,n;
	scanf("%d",&t);
	while(t--) {
		scanf("%d",&n);
		int g=gcd(n,180);
		int temp=n,tempp=180;
		temp/=g,tempp/=g;
		if(temp==tempp-1) temp*=2,tempp*=2;
		printf("%d\n",tempp);
	}
	return 0;
}

D - Easy Problem

Easy。。确实是Easy啊，直接DP，设f[i][j]表示前i位匹配了hard的前j个字符，最小的代价，然后瞎转移一通就好了。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<cmath>
#include<cctype>
using namespace std;

typedef long long ll;
const int Maxn=210000;

int n,a[Maxn];
ll f[Maxn][4];
char s[Maxn];

int main() {
	scanf("%d",&n);
	scanf("%s",s);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	memset(f,0x3f,sizeof(f));
	f[0][0]=0;
	for(int i=1;i<=n;i++) {
		switch(s[i-1]) {
			case 'h' : {
				f[i][0]=f[i-1][0]+a[i];
				f[i][1]=min(f[i-1][1],f[i-1][0]);
				f[i][2]=f[i-1][2];
				f[i][3]=f[i-1][3];
				break;
			}
			case 'a' : {
				f[i][0]=f[i-1][0];
				f[i][1]=f[i-1][1]+a[i];
				f[i][2]=min(f[i-1][2],f[i-1][1]);
				f[i][3]=f[i-1][3];
				break;
			}
			case 'r' : {
				f[i][0]=f[i-1][0];
				f[i][1]=f[i-1][1];
				f[i][2]=f[i-1][2]+a[i];
				f[i][3]=min(f[i-1][3],f[i-1][2]);
				break;
			}
			case 'd' : {
				f[i][0]=f[i-1][0];
				f[i][1]=f[i-1][1];
				f[i][2]=f[i-1][2];
				f[i][3]=f[i-1][3]+a[i];
				break;
			}
			default : {
				f[i][0]=f[i-1][0];
				f[i][1]=f[i-1][1];
				f[i][2]=f[i-1][2];
				f[i][3]=f[i-1][3];
				break;
			}
		}
	}
	printf("%I64d\n",min(f[n][0],min(f[n][1],min(f[n][2],f[n][3]))));
	return 0;
}

G - Lucky Tickets

这好像还是我第一次做生成函数的题啊，因为被C卡了太长时间，所以做这道题的时候还剩半个小时了。看到这道题很容易想到可以背包，然后我刚想开始写，结果发现背包复杂度很明显不对啊，还有这个模数为什么是998244353呢？然后立刻就想到可以做多项式的幂函数，然而这个时间复杂度是\(O(n\log^2n)\)的吧，当然还有\(O(n\log n)\)的但是我不会啊，这怎么办啊，n最大可能到1e6肯定要超时了，但是现在也没有时间了，还不如试试，于是写完了之后调过样例直接交，然后就A了。

考完后我发现极限数据本地是6秒，然而cf上是3秒，说明了cf是真的快。。。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<cmath>
#include<cctype>
using namespace std;

typedef long long ll;
const int Maxn=2100000;
const int mod=998244353;
const ll gg=3;
const ll gi=332748118;

int limit,l,r[Maxn],a[Maxn],n,k;
ll b[Maxn],f[Maxn],ans,c[Maxn];

ll powp(ll a,ll b) {
	ll ans=1;
	while(b) {
		if(b&1) ans=ans*a%mod;
		a=a*a%mod;
		b>>=1;
	}
	return ans;
}

void ntt(ll *a,ll gg) {
	for(int i=0;i<limit;i++) if(i<r[i]) swap(a[i],a[r[i]]);
	for(int mid=1;mid<limit;mid<<=1) {
		ll Wn=powp(gg,(mod-1)/(mid<<1));
		for(int j=0;j<limit;j+=mid<<1) {
			ll w=1;
			for(int k=0;k<mid;k++,w=w*Wn%mod) {
				ll x=a[j+k],y=w*a[j+k+mid]%mod;
				a[j+k]=(x+y)%mod;
				a[j+k+mid]=(x-y+mod)%mod;
			}
		}
	}
}

void powp(ll *a,int n) {
	int temp=::a[k],tempp=0;
	b[0]=1;
	while(n) {
		if(n&1) {
			tempp+=temp;limit=1,l=0;
			while(limit<=tempp) limit<<=1,l++;
			for(int i=0;i<limit;i++) r[i]=r[i>>1]>>1|((i&1)<<l-1);
			for(int i=0;i<limit;i++) c[i]=a[i];
			ntt(b,gg),ntt(c,gg);
			for(int i=0;i<limit;i++) b[i]=c[i]*b[i]%mod;
			ntt(b,gi);
			ll inv=powp(limit,mod-2);
			for(int i=0;i<limit;i++) b[i]=b[i]*inv%mod;
		}
		temp<<=1;limit=1,l=0;
		while(limit<=temp) limit<<=1,l++;
		for(int i=0;i<limit;i++) r[i]=r[i>>1]>>1|((i&1)<<l-1);
		ntt(a,gg);
		for(int i=0;i<limit;i++) a[i]=a[i]*a[i]%mod;
		ntt(a,gi);
		ll inv=powp(limit,mod-2);
		for(int i=0;i<limit;i++) a[i]=a[i]*inv%mod;
		n>>=1;
	}
}

int main() {
	scanf("%d%d",&n,&k);
	for(int i=1;i<=k;i++) scanf("%d",&a[i]);
	sort(a+1,a+k+1);
	for(int i=1;i<=k;i++) f[a[i]]=1;
	n>>=1;powp(f,n);
	for(int i=0;i<=a[k]*n;i++)
		ans=(ans+1ll*b[i]*b[i])%mod;
	printf("%I64d",ans);
	return 0;
}