[luogu 2458][SDOI2006]保安站岗

题目描述

五一来临，某地下超市为了便于疏通和指挥密集的人员和车辆，以免造成超市内的混乱和拥挤，准备临时从外单位调用部分保安来维持交通秩序。

已知整个地下超市的所有通道呈一棵树的形状；某些通道之间可以互相望见。总经理要求所有通道的每个端点（树的顶点）都要有人全天候看守，在不同的通道端点安排保安所需的费用不同。

一个保安一旦站在某个通道的其中一个端点，那么他除了能看守住他所站的那个端点，也能看到这个通道的另一个端点，所以一个保安可能同时能看守住多个端点（树的结点），因此没有必要在每个通道的端点都安排保安。

编程任务：

请你帮助超市经理策划安排，在能看守全部通道端点的前提下，使得花费的经费最少。

输入输出格式

输入格式：

第1行 n，表示树中结点的数目。

第2行至第n+1行，每行描述每个通道端点的信息，依次为：该结点标号i（0<i<=n），在该结点安置保安所需的经费k（<=10000），该边的儿子数m，接下来m个数，分别是这个节点的m个儿子的标号r1，r2，...，rm。

对于一个n（0 < n <= 1500）个结点的树，结点标号在1到n之间，且标号不重复。

输出格式：

最少的经费。

如右图的输入数据示例

输出数据示例：

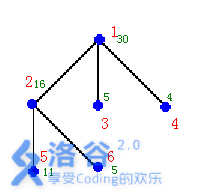
输入输出样例

输入样例#1： 复制

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

输出样例#1： 复制

25

说明

样例说明：在结点2，3，4安置3个保安能看守所有的6个结点，需要的经费最小：25

题解

树形dp经典题...同时贪心也可以做的，不过树形dp是$O(n)$，贪心是$O(nlogn)$

（可以算是四倍经验题了）

贪心做法可以看我这篇题解

这里讲树形dp做法

我们可以设$f[x][0]$被子节点控制，$f[x][1]$被自己控制，$f[x][2]$被父亲控制

那么显然$f[i][x]$可以从子节点中三个状态任意一个转移过来，所以

$f[x][1]+=min(f[e[i].to][0],min(f[e[i].to][1],f[e[i].to][2]))$

$f[x][2]$可以从子节点中除了被父亲控制的那个节点转移过来

$f[x][2]+=min(f[e[i].to][1],f[e[i].to][0])$

比较难办的是$f[x][0]$的转移

因为只要有一个子节点有人那么其他子节点都可以不放人了

有一个很妙的做法

如果在这个子节点放人比不放人更优，那肯定就不放人了，顺便标记一下

否则存下来放人与不放人的差值，对所有的差值取个min

到最后如果没有被标记就加上这个差值

转移方程为

$f[x][0]+=min(f[e[i].to][0],f[e[i].to][1])$

#include <bits/stdc++.h>

using namespace std;

int n;
int head[],c[],cnt;
int f[][];
//f[i][0]被子节点控制，f[i][1]被自己控制，f[i][2]被父亲控制 

struct edge {
    int to,nxt;
}e[];

void ins(int u,int v){
    e[++cnt].to=v;e[cnt].nxt=head[u];head[u]=cnt;
    e[++cnt].to=u;e[cnt].nxt=head[v];head[v]=cnt;
}

#define inf 0x3f3f3f3f

void dfs(int x,int fa){
    f[x][]=c[x];
    f[x][]=f[x][]=;
    int cnt=,tx=inf;
    for(int i=head[x];i;i=e[i].nxt){
        if(e[i].to==fa)continue;
        dfs(e[i].to,x);
        f[x][]+=min(f[e[i].to][],min(f[e[i].to][],f[e[i].to][]));
        f[x][]+=min(f[e[i].to][],f[e[i].to][]);
        if(f[e[i].to][]<f[e[i].to][])cnt=;
        else tx=min(tx,f[e[i].to][]-f[e[i].to][]);
        f[x][]+=min(f[e[i].to][],f[e[i].to][]);
    }
    if(!cnt)f[x][]+=tx;
}

int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        int x;
        scanf("%d",&x);
        scanf("%d",&c[x]);
        int m;
        scanf("%d",&m);
        for(int j=;j<=m;j++){
            int y;
            scanf("%d",&y);
            ins(x,y);
        }
    }
    dfs(,);
    printf("%d\n",min(f[][],f[][]));
}