2016年第七届蓝桥杯C/C++B组省赛题目解析

题目1：煤球数目

有一堆煤球，堆成三角棱锥形。具体：
第一层放1个，
第二层3个（排列成三角形），
第三层6个（排列成三角形），
第四层10个（排列成三角形），
....
如果一共有100层，共有多少个煤球？
请填表示煤球总数目的数字。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

解析：

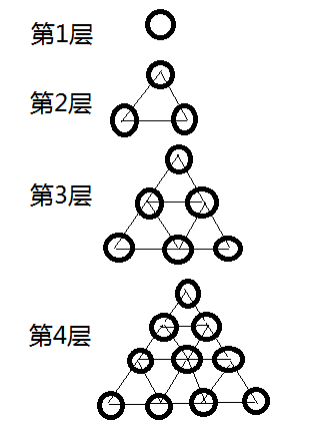
第一层：1个。

第二层：2*3-3=3个。

第三层：3*3-3=6个。

第四层：4*3-3=10个。

代码如下：

    int s=,a=;

    for(int i=;i<=;i++){

        a=a+i;

        s=s+a;

    }

    printf("%d\n",s);

答案：171700

其他参考代码

    int a[];

    int i,sum;

    a[]=;

    for(i=;i<=;++i)

        a[i]=a[i-]+i;

    sum=;

    for(i=;i<=;++i)

        sum=sum+a[i];

    printf("%d\n",sum);

    return ;

题目2：生日蜡烛

某君从某年开始每年都举办一次生日party，并且每次都要吹熄与年龄相同根数的蜡烛。
现在算起来，他一共吹熄了236根蜡烛。
请问，他从多少岁开始过生日party的？
请填写他开始过生日party的年龄数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

分析：

此题可以通过两个for循环实现，第一遍从他0岁开始循环，然后一步步累加到他现在的年龄，再通过if语句判断其是否在这个年龄段里吹熄了236根蜡烛。如果是，则输出最初的年龄，如果不是，则返回第一步继续循环。

代码如下：

    int newage,oldage,sum;  //newage为开始过生日party的年龄，oldage为现在的年龄

    for(newage=;newage<;++newage){

        sum=;

        for(oldage=newage;oldage<;++oldage){

            sum=sum+oldage;

            if(sum==)  //判断吹灭的蜡烛总数

                printf("%d,%d\n",newage,oldage);

        }

    }

    return ;

答案：26

题目3：凑算式

这个算式中A~I代表0~9的数字，不同的字母代表不同的数字。
比如： 6+8/3+952/714 就是一种解法， 5+3/1+972/486 是另一种解法。
这个算式一共有多少种解法？
注意：你提交应该是个整数，不要填写任何多余的内容或说明性文字。
修正：A~I代表1~9的数字

分析：

此题可以用9个for循环挨个穷举出来，中间用if判断是否有重复的数字，最后用if判断等式是否成立。

代码如下：

    int A,B,C,D,E,F,G,H,I;  //九个不重复的数字 

    int sum1,sum2,sum3,sum4;  //四个多项式 

    int ans;  //统计解法 

    ans=;

    for(A=;A<=;++A){

        for(B=;B<=;++B){

            if(B==A)continue;

            for(C=;C<=;++C){

                if(C==A||C==B)continue;

                for(D=;D<=;++D){

                    if(D==A||D==B||D==C)continue;

                    for(E=;E<=;++E){

                        if(E==A||E==B||E==C||E==D)continue;

                        for(F=;F<=;++F){

                            if(F==A||F==B||F==C||F==D||F==E)continue;

                            for(G=;G<=;++G){

                                if(G==A||G==B||G==C||G==D||G==E||G==F)continue;

                                for(H=;H<=;++H){

                                    if(H==A||H==B||H==C||H==D||H==E||H==F||H==G)continue;

                                    for(I=;I<=;++I){

                                        if(I==A||I==B||I==C||I==D||I==E||I==F||I==G||I==H)continue;

                                        sum1=A*C*(G*+H*+I);

                                        sum2=B*(G*+H*+I);

                                        sum3=(D*+E*+F)*C;

                                        sum4=*C*(G*+H*+I);

                                        //注意，要将题中的等式通分

                                        if(sum1+sum2+sum3==sum4){

                                            ++ans;

                                        }

                                    }

                                }

                            }

                        }

                    }

                }

            }

        }

    }

    printf("%d\n",ans);

    return ;

凑算式

答案：29。

题目4：快速排序

排序在各种场合经常被用到。
快速排序是十分常用的高效率的算法。
其思想是：先选一个“标尺”，
用它把整个队列过一遍筛子，
以保证：其左边的元素都不大于它，其右边的元素都不小于它。
这样，排序问题就被分割为两个子区间。
再分别对子区间排序就可以了。
下面的代码是一种实现，请分析并填写划线部分缺少的代码。

注意：只填写缺少的内容，不要书写任何题面已有代码或说明性文字。

代码如下：

#include <stdio.h>

void swap(int a[], int i, int j)

{

    int t = a[i];

    a[i] = a[j];

    a[j] = t;

}

int partition(int a[], int p, int r)

{

    int i = p;

    int j = r + ;

    int x = a[p];

    while(){

        while(i<r && a[++i]<x);

        while(a[--j]>x);

        if(i>=j) break;

        swap(a,i,j);

    }

    //______________________;

    swap(a,p,j);

    return j;

}

void quicksort(int a[], int p, int r)  //快排

{

    if(p<r){

        int q = partition(a,p,r);

        quicksort(a,p,q-);

        quicksort(a,q+,r);

    }

}

int main()

{

    int i;

    int a[] = {,,,,,,,,,,,};

    int N = ;

    quicksort(a, , N-);

    for(i=; i<N; i++) printf("%d ", a[i]);

    printf("\n");

    return ;

}

快速排序

题目5：抽签

X星球要派出一个5人组成的观察团前往W星。
其中：
A国最多可以派出4人。
B国最多可以派出2人。
C国最多可以派出2人。
....
那么最终派往W星的观察团会有多少种国别的不同组合呢？
下面的程序解决了这个问题。
数组a[] 中既是每个国家可以派出的最多的名额。
程序执行结果为：
DEFFF
CEFFF
CDFFF
CDEFF
CCFFF
CCEFF
CCDFF
CCDEF
BEFFF
BDFFF
BDEFF
BCFFF
BCEFF
BCDFF
BCDEF
....
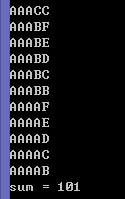
(以下省略，总共101行)

仔细阅读代码，填写划线部分缺少的内容。
注意：不要填写任何已有内容或说明性文字。

分析：

对于f(int a[],int k,int m,char b[]).a[] 是每个国度的最多指派人数,k表现当前是哪个国度,m表现还须要派送几小我私家(可认为负数).b表现已经派送的人的字符串。
以是这个问题在递归中心的的第一个轮回表现从0~a[i]中让i国选择指派人数，内轮回只是向b[]记载的历程。

代码如下：

#include <stdio.h>

#define N 6

#define M 5

#define BUF 1024

int sum=;  //sum为组合种类

void f(int a[], int k, int m, char b[])

{

    int i,j;

    if(k==N){

        b[M] = ;

        if(m==){

            printf("%s\n",b);

            ++sum;

        }

        return;

    }

    for(i=; i<=a[k]; i++){

        for(j=; j<i; j++) b[M-m+j] = k+'A';

        //______________________;  //填空位置

        //f(a,k+1,m-i,b);

        f(a,k+,m-j,b);

    }

}

int main()

{

    int  a[N] = {,,,,,};

    char b[BUF];

    f(a,,M,b);

    printf("sum = %d\n",sum);

    return ;

}

抽签

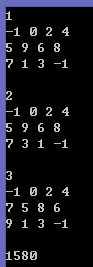
题目6：方格填数

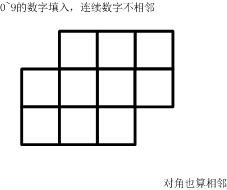
方格填数如下的10个格子 +--+--+--+ | | | | +--+--+--+--+ | | | | | +--+--+--+--+ | | | | +--+--+--+
（如果显示有问题，也可以参看图）
填入0~9的数字。
要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）
一共有多少种可能的填数方案？
请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

代码如下：

#include<stdio.h>

#include<string.h>

#include<math.h>

#include<algorithm>

int a[][];

bool used[];

int sum;

void display(){

    for(int i=;i<=;++i){

        for(int j=;j<=;++j){

            printf("%d ",a[i][j]);

        }

        printf("\n");

    }

    printf("\n");

}

void dfs(int i,int j){

    if(i==&&j==){

        ++sum;

        if(sum<=){

            printf("%d\n",sum);

            display();

        }

        return;

    }

    int k;

    int mi,mj;

    int mmi,mmj;

    bool flag;

    for(k=;k<=;++k){

        if(used[k])continue;

        flag=true;

        for(mi=-;mi<=;++mi){

            for(mj=-;mj<=;++mj){

                mmi=i+mi;

                mmj=j+mj;

                if( <=mmi&&mmi<= && <=mmj&&mmj<= ){

                    if(a[mmi][mmj]!=-){

                        if(abs(k-a[mmi][mmj])==){

                            flag=false;

                            break;

                        }

                    }

                }

            }

            if(flag==false)break;

        }

        if(flag){

            a[i][j]=k;

            used[k]=true;

            if(j==){

                dfs(i+,);

            }

            else{

                dfs(i,j+);

            }

            a[i][j]=-;

            used[k]=false;

        }

    }

}

int main(){

    memset(used,false,sizeof(used));

    memset(a,-,sizeof(a));

    sum=;

    dfs(,);

    printf("%d\n",sum);

    return ;

}

方格填数

题目7：剪邮票

如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。
请你计算，一共有多少种不同的剪取方法。
请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

分析：

可以先把所有五个数的组合找出来，然后再判断是否可行。

代码如下：

#include<stdio.h>

#include<string.h>

#include<algorithm>

using namespace std;

bool vis[][];

bool exist[][][][][];  //标志这5个位置是否搜过

int a[];  //记录访问的5个位置

int b[];  //5个位置排序

int sum;

void dfs(int m){

    if(m==){

        for(int i=;i<=;++i){

            b[i]=a[i];

        }

        sort(b+,b++);//5个位置排序

        if(exist[b[]][b[]][b[]][b[]][b[]]){//看看这5个位置有没有搜过

            return;

        }

        printf("%d %d %d %d %d\n",b[],b[],b[],b[],b[]);

        exist[b[]][b[]][b[]][b[]][b[]]=true;  //判断重复

        ++sum;

        return;

    }

    int i,j;

    int i1,i2;

    int j1,j2;

    bool flag;

    for(i=;i<;++i){

        for(j=;j<;++j){

            if(vis[i][j])continue;//已经选择了

            //如果是第一个，那么直接选

            if(m==){

                vis[i][j]=true;

                a[m]=i*+j;  //记录位置

                dfs(m+);

                vis[i][j]=false;

                continue;

            }

            //否则，必需当上、下、左、右四个位置中至少有一个位置已选择时，才能选

            i1=i-;

            i2=i+;

            j1=j-;

            j2=j+;

            flag=false;

            if(i1>=){

                if(vis[i1][j]){

                    flag=true;

                }

            }

            if(i2<){

                if(vis[i2][j]){

                    flag=true;

                }

            }

            if(j1>=){

                if(vis[i][j1]){

                    flag=true;

                }

            }

            if(j2<){

                if(vis[i][j2]){

                    flag=true;

                }

            }

            if(flag){//这个位置可以选了

                vis[i][j]=true;

                a[m]=i*+j;//记录位置

                dfs(m+);

                vis[i][j]=false;

            }

        }

    }

}

int main(){

    memset(vis,false,sizeof(vis));

    memset(exist,false,sizeof(exist));

    sum=;

    dfs();

    printf("sum = %d\n",sum);

    return ;

}

剪邮票

题目8：四平方和

四平方和定理，又称为拉格朗日定理：
每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去，就正好可以表示为4个数的平方和。
比如：
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2
（^符号表示乘方的意思）
对于一个给定的正整数，可能存在多种平方和的表示法。
要求你对4个数排序：
0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列，最后输出第一个表示法
程序输入为一个正整数N (N<5000000)
要求输出4个非负整数，按从小到大排序，中间用空格分开
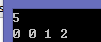
例如，输入：
5
则程序应该输出：
0 0 1 2
再例如，输入：
12
则程序应该输出：
0 2 2 2
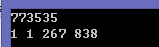
再例如，输入：
773535
则程序应该输出：
1 1 267 838
资源约定：
峰值内存消耗 < 256M
CPU消耗 < 3000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>，不能通过工程设置而省略常用头文件。
提交时，注意选择所期望的编译器类型。

代码如下：

#include<iostream>

#include<stdio.h>

#include<math.h>

using namespace std;

const int MAXN=;

int pow_2[];

int main(){

    int N;

    int i;

    int a,b,c,d;

    int sum;

    bool flag;

    int p,q;

    for(i=;i<;++i){

        pow_2[i]=i*i;

    }

    while(~scanf("%d",&N)){

        flag=false;

        sum=;

        for(a=;a<MAXN;++a){

            sum=pow_2[a];

            for(b=a;b<MAXN;++b){

                sum=sum+pow_2[b];

                if(sum>N){

                    sum=sum-pow_2[b];

                    continue;

                }

                for(c=b;c<MAXN;++c){

                    sum=sum+pow_2[c];

                    if(sum>N){

                        sum=sum-pow_2[c];

                        continue;

                    }

                    p=N-sum;

                    q=sqrt(p);

                    if(pow_2[q]==p){

                        printf("%d %d %d %d\n",a,b,c,q);

                        flag=true;

                        break;

                    }

                    else{

                        sum=sum-pow_2[c];

                    }

                }

                sum=sum-pow_2[b];

                if(flag)break;

            }

            sum=sum-pow_2[a];

            if(flag)break;

        }

    }

    return ;

}

四平方和

题目9：交换瓶子

有N个瓶子，编号 1 ~ N，放在架子上。
比如有5个瓶子：
2 1 3 5 4
要求每次拿起2个瓶子，交换它们的位置。
经过若干次后，使得瓶子的序号为：
1 2 3 4 5
对于这么简单的情况，显然，至少需要交换2次就可以复位。
如果瓶子更多呢？你可以通过编程来解决。
输入格式为两行：
第一行: 一个正整数N（N<10000）, 表示瓶子的数目
第二行：N个正整数，用空格分开，表示瓶子目前的排列情况。
输出数据为一行一个正整数，表示至少交换多少次，才能完成排序。
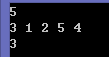
例如，输入：
5
3 1 2 5 4
程序应该输出：
3
再例如，输入：
5
5 4 3 2 1
程序应该输出：
2
资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>，不能通过工程设置而省略常用头文件。
提交时，注意选择所期望的编译器类型。

分析：

从位置1枚举到N，如果编号不对，那么就与对应位置的瓶子交换。

代码如下：

#include<iostream>

#include<stdio.h>

using namespace std;

int a[];//a[i]表示位置i的瓶子编号

int b[];//b[i]表示i号瓶子的位置。没有这个数组的话，需要在a数组中循环找到i号瓶子（O(n)），用这个数组的话是O(1)

int main(){

    int N;

    int i;

    int id;

    int sum;

    //设瓶子1为位置i的瓶子，瓶子2为i号瓶子

    int id1,id2;  //瓶子1的编号，瓶子2的编号

    int pos1,pos2;//瓶子1的位置，瓶子2的位置

    while(~scanf("%d",&N)){

        for(i=;i<=N;++i){

            scanf("%d",&id);

            a[i]=id;//位置i放id号瓶子

            b[id]=i;//id号瓶子放到位置i

        }

        sum=;

        for(i=;i<=N;++i){//位置从1遍历到N

            if(a[i]==i)continue;//位置i放的是i号瓶子

            //否则，瓶子2与瓶子1交换

            id1=a[i];

            pos1=i;

            id2=i;

            pos2=b[i];//没有b数组的话，需要在a数组中找到i号瓶子

            ++sum;

            //瓶子1放到瓶子2的位置

            a[pos2]=id1;//瓶子2的位置（pos2）放瓶子1（id1）

            b[id1]=pos2;//瓶子1（id1）放到瓶子2的位置（pos2）

            //瓶子2放到瓶子1的位置

            a[pos1]=id2;//瓶子1的位置放瓶子2

            b[id2]=pos1;//瓶子2放到瓶子1的位置

        }

        printf("%d\n",sum);

    }

    return ;

}

交换瓶子-贪心

#include<iostream>

#include<stdio.h>

using namespace std;

int sum;

void SelectSort(int R[],int n){

    int i,j,k;

    int tmp;

    for(i=;i<n-;++i){//做第i趟排序

        k=i;

        for(j=i+;j<n;++j){//在当前无序区R[i..n-1]中选最小的R[k]

            if(R[j]<R[k])k=j;//k记下目前找到的最小关键字所在的位置

        }

        if(k!=i){//交换R[i]和R[k]

            tmp=R[i];

            R[i]=R[k];

            R[k]=tmp;

            ++sum;

        }

    }

}

int main(){

    int N;

    int a[];

    int i;

    while(~scanf("%d",&N)){

        for(i=;i<N;++i){

            scanf("%d",&a[i]);

        }

        sum=;

        SelectSort(a,N);

        printf("%d\n",sum);

    }

    return ;

}

交换瓶子-选择排序

题目10：最大比例

X星球的某个大奖赛设了M级奖励。每个级别的奖金是一个正整数。
并且，相邻的两个级别间的比例是个固定值。
也就是说：所有级别的奖金数构成了一个等比数列。比如：
16,24,36,54
其等比值为：3/2
现在，我们随机调查了一些获奖者的奖金数。
请你据此推算可能的最大的等比值。
输入格式：
第一行为数字N，表示接下的一行包含N个正整数
第二行N个正整数Xi(Xi<1 000 000 000 000)，用空格分开。每个整数表示调查到的某人的奖金数额
要求输出：
一个形如A/B的分数，要求A、B互质。表示可能的最大比例系数
测试数据保证了输入格式正确，并且最大比例是存在的。
例如，输入：
3
1250 200 32
程序应该输出：
25/4
再例如，输入：
4
3125 32 32 200
程序应该输出：
5/2
再例如，输入：
3
549755813888 524288 2
程序应该输出：
4/1
资源约定：
峰值内存消耗 < 256M
CPU消耗 < 3000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>，不能通过工程设置而省略常用头文件。
提交时，注意选择所期望的编译器类型。

代码如下：

#include <stdio.h>

#include <algorithm>

#include <queue>

using namespace std;

#define LL long long

struct fs

{

    LL up,down;

};

int n;

LL arr[];

fs Fs[];  

bool cmp(LL a,LL b)

{

    return a > b;

}  

LL Gcd(LL a,LL b)

{

    if( b ==  )return a;

    return Gcd(b,a%b);

}

LL Get(LL a, LL b)

{

    if( a < b) a ^= b ^= a ^= b;

    LL v[];

    queue<LL>team;

    if( a == b || a / b == a) return b;

    v[] = a, v[] = b;

    v[] = a / b;

    int top = ,i,j;

    team.push(a/b);

    while(team.size())

    {

        LL now = team.front();

        team.pop();

        for(i =  ; i < top ; i ++)

        {

            LL temp = (v[i] > now) ? v[i] / now : now / v[i];

            bool find = false;

            for(j =  ; j < top ; j ++)

                if( v[j] == temp) find = true;

            if(find == true) continue;

            team.push(temp);

            v[top++] = temp;

        }

    }

    LL ans = v[];

    for(i =  ; i < top ; i ++)

        if(v[i] != )

        {

            ans = v[i];

            break;

        }

    for(i =  ; i < top ; i ++)

        if( v[i] < ans && v[i] != ) ans = v[i];

    return ans;

}

int main()

{

    int i,j;

    scanf("%d",&n);

    for(i =  ; i < n ; i ++) scanf("%lld",&arr[i]);

    sort(arr,arr+n,cmp);

    int top = ;

    for(i = ; i < n ; i ++)

        if(arr[i] != arr[i-]) arr[top++] = arr[i];

    n = top;

    for(i =  ; i < n - ; i ++)

    {

        LL gcd = Gcd(arr[i],arr[i+]);

        Fs[i].up = arr[i] / gcd;

        Fs[i].down = arr[i+] / gcd;

    }

    LL x = Fs[].up;

    for(i =  ; i < n -  ; i ++)

        x = Get(x,Fs[i].up);

    LL y = Fs[].down;

    for(i =  ; i < n - ; i ++)

        y = Get(y,Fs[i].down);

    printf("%lld/%lld\n",x,y);

    return ;

}

最大比例