机器学习【算法】：KNN近邻

引言

　　本文讨论的kNN算法是监督学习中分类方法的一种。所谓监督学习与非监督学习，是指训练数据是否有标注类别，若有则为监督学习，若否则为非监督学习。监督学习是根据输入数据（训练数据）学习一个模型，能对后来的输入做预测。在监督学习中，输入变量与输出变量可以是连续的，也可以是离散的。若输入变量与输出变量均为连续变量，则称为回归；输出变量为有限个离散变量，则称为分类；输入变量与输出变量均为变量序列，则称为标注

　　有监督的分类学习

KNN算法的基本要素大致有三个：

　　1、K 值的选择（即输入新实例要取多少个训练实例点作为近邻）

　　2、距离的度量（欧氏距离，曼哈顿距离等）

　　3、分类决策规则（常用的方式是取k个近邻训练实例中类别出现次数最多者作为输入新实例的类别）

使用方式：

　　K 值会对算法的结果产生重大影响。K值较小意味着只有与输入实例较近的训练实例才会对预测结果起作用，容易发生过拟合；如果 K 值较大，优点是可以减少学习的估计误差，缺点是学习的近似误差增大，这时与输入实例较远的训练实例也会对预测起作用，是预测发生错误。在实际应用中，K 值一般选择一个较小的数值，通常采用交叉验证的方法来选择最有的 K 值。随着训练实例数目趋向于无穷和 K=1 时，误差率不会超过贝叶斯误差率的2倍，如果K也趋向于无穷，则误差率趋向于贝叶斯误差率。

　　距离度量一般采用 Lp 距离，当p=2时，即为欧氏距离，在度量之前，应该将每个属性的值规范化，这样有助于防止具有较大初始值域的属性比具有较小初始值域的属性的权重过大（规范）

　　算法中的分类决策规则往往是多数表决，即由输入实例的 K 个最临近的训练实例中的多数类决定输入实例的类别

简述

　　KNN分类算法，是理论上比较成熟的方法，也是最简单的机器学习算法之一。

　　该方法的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

　　KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

　　一个对于KNN算法解释最清楚的图如下所示：

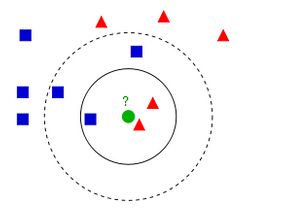
　　蓝方块和红三角均是已有分类数据，当前的任务是将绿色圆块进行分类判断，判断是属于蓝方块或者红三角。

　　当然这里的分类还跟K值是有关的：

　　如果K=3(实线圈)，红三角占比2/3，则判断为红三角；

　　如果K=5(虚线圈)，蓝方块占比3/5，则判断为蓝方块。

　　由此可以看出knn算法实际上根本就不用进行训练，而是直接进行计算的，训练时间为0，计算时间为训练集规模n。

　　knn算法在分类时主要的不足是，当样本不平衡时，如果一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的 K 个邻居中大容量类的样本占多数。

*算法实现

1、函数

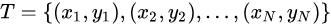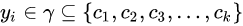输入：训练数据集，其中为训练实例的特征向量（ $x$ i为特征值），为训练实例的类别（ $y$ i为 $x$ i对应的类别）

输出：新输入实例 $x$ 所属类别 $y$ （实例类别）

1、根据给定的距离度量，在训练集T中找到与 $x$ 最近的k个点，涵盖这k个点的邻域记为 $N_k(x)$ （上图中实体圆圈包含的数据）

2、在 $N_k(x)$ 中根据分类决策规则（如多数表决）决定 $x$ 所属的类别 $y$ （即统计 $N_k(x)$ 哪个 $y$ 类别出现的次数多，则取哪个）：

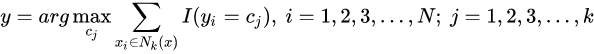
其中I为指示函数，仅当 $y_i = c_j$ 时I(*)的值为1，否则为0.（argmax公式表示后面取值最大时，Cj的变量值，公式的目的也是求此值； $x$ i为 $N_k(x)$ 中的值，Cj为涵盖领域存在的类别；利用求和公式∑，当Cj为C1时， $x$ i∈ $N_k(x)$ 分别代入，得出值; $x$ i为已知数据，Cj值不断变化,求出公式的最大值，得出最终 $y$ 得取值）

2、距离度量方式

较为常用的距离度量方式是欧式距离，定义可以使用其他更为一般的 $L_p$ 距离或闵科夫斯基（Minkowski）距离。

设特征空间 $\chi$ 为n为实数向量空间 $R^n$ ， $x_i,x_j \in \chi,x_i=(x^{(1)}_i,x^{(2)}_i,x^{(3)}_i,...,x^{(n)}_i)^T$ ， $x_j=(x^{(1)}_j,x^{(2)}_j,x^{(3)}_j,...,x^{(n)}_j)^T$ ， $x_i,x_j$ 的 $L_p$ 距离可定义为：

　　 $L_p(x_i,x_j) = (\sum_{l=1}^{n}{|x_i^{(l)}-x_j^{(l)}|^p} )^{1/p}$ 　　　　闵科夫斯基距离

　　 $L_p(x_i,x_j) = (\sum_{l=1}^{n}{|x_i^{(l)}-x_j^{(l)}|^2} )^{1/2}$ 　　　　欧氏距离，p取2

　　 $L_p(x_i,x_j) = \sum_{l=1}^{n}{|x_i^{(l)}-x_j^{(l)}} |$ 　　　　　　　曼哈顿距离，p取1

　　 $L_p(x_i,x_j) = \max \limits_l {|x_i^{(l)}-x_j^{(l)}} |$ 　　　　　　 p取 $\infty$

3、K值选择

　　一般会先选择较小的k值，然后进行交叉验证选取最优的k值。k值较小时，整体模型会变得复杂，且对近邻的训练实例点较为敏感，容易出现过拟合。k值较大时，模型则会趋于简单，此时较远的训练实例点也会起到预测作用，容易出现欠拟合，特殊的，当k取N时，此时无论输入实例是什么，都会将其预测为属于训练实例中最多的类别。

4、分类决策规则

　　KNN学习模型：输入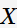

　　通过学习得到决策函数：输出类别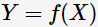

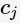假设分类损失函数为0-1损失函数，即分类正确时损失函数值为0，分类错误时则为1。假如给预测类别为,即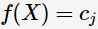；同时由式子（1）可知k邻域的样本点对学习模型的贡献度是均等的，则kNN学习模型误分类率为

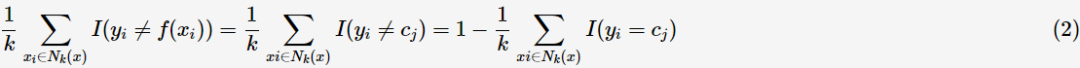
若要最小化误分类率，则应

所以，最大表决规则等价于经验风险最小化。

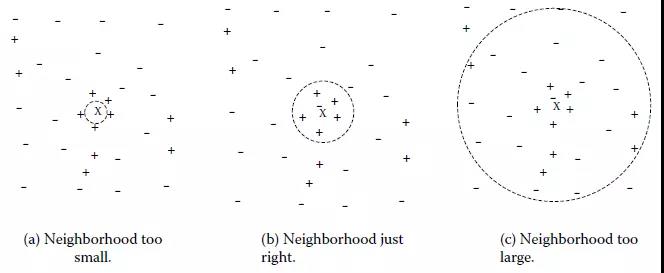
k值得选取对kNN学习模型有着很大的影响。若k值过小，预测结果会对噪音样本点显得异常敏感。特别地，当k等于1时，kNN退化成最近邻算法，没有了显式的学习过程。若k值过大，会有较大的邻域训练样本进行预测，可以减小噪音样本点的减少；但是距离较远的训练样本点对预测结果会有贡献，以至于造成预测结果错误。下图给出k值的选取对于预测结果的影响：

前面提到过，k邻域的样本点对预测结果的贡献度是相等的；但距离更近的样本点应有更大的相似度，其贡献度应比距离更远的样本点大。可以加上权值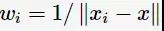进行修正，则最大表决原则变成：

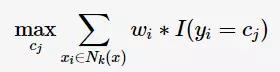
应用案例

对data2.txt中的数据进行运算，取前10%的数据进行验证，90%的数据做训练，根据K值的不同，算出误差率，选出最佳K值；

    8.326976    0.953952

    7.153469    1.673904

    1.441871    0.805124

    13.147394    0.428964

    1.669788    0.134296

    10.141740    1.032955

    6.830792    1.213192

    13.276369    0.543880

    8.631577    0.749278

    12.273169    1.508053

    3.723498    0.831917

    8.385879    1.669485

    4.875435    0.728658

    4.680098    0.625224

    15.299570    0.331351

    1.889461    0.191283

    7.516754    1.269164

    14.239195    0.261333

    0.000000    1.250185

    10.528555    1.304844

    3.540265    0.822483

    2.991551    0.833920

    5.297865    0.638306

    6.593803    0.187108

    2.816760    1.686209

    12.458258    0.649617

    0.000000    1.656418

    9.968648    0.731232

    1.364838    0.640103

    0.230453    1.151996

    11.865402    0.882810

    0.120460    1.352013

    8.545204    1.340429

    5.856649    0.160006

    9.665618    0.778626

    9.778763    1.084103

    4.932976    0.632026

    2.216246    0.587095

    14.305636    0.632317

    12.591889    0.686581

    3.424649    1.004504

    0.000000    0.147573

    8.533823    0.205324

    9.829528    0.238620

    11.492186    0.263499

    3.570968    0.832254

    1.771228    0.207612

    3.513921    0.991854

    4.398172    0.975024

    4.276823    1.174874

    5.946014    1.614244

    13.798970    0.724375

    10.393591    1.663724

    3.007577    0.297302

    1.031938    0.486174

    4.751212    0.064693

    3.692269    1.655113

    10.448091    0.267652

    10.585786    0.329557

    1.604501    0.069064

    3.679497    0.961466

    3.795146    0.696694

    2.531885    1.659173

    9.733340    0.977746

    6.093067    1.413798

    7.712960    1.054927

    11.470364    0.760461

    2.886529    0.934416

    10.054373    1.138351

    9.972470    0.881876

    2.335785    1.366145

    11.375155    1.528626

    0.000000    0.605619

    4.126787    0.357501

    6.319522    1.058602

    8.680527    0.086955

    14.856391    1.129823

    2.454285    0.222380

    7.292202    0.548607

    8.745137    0.857348

    8.579001    0.683048

    2.507302    0.869177

    11.415476    1.505466

    4.838540    1.680892

    10.339507    0.583646

    6.573742    1.151433

    6.539397    0.462065

    2.209159    0.723567

    11.196378    0.836326

    4.229595    0.128253

    9.505944    0.005273

    8.652725    1.348934

    17.101108    0.490712

    7.871839    0.717662

    8.262131    1.361646

    9.015635    1.658555

    9.215351    0.806762

    6.375007    0.033678

    2.262014    1.022169

    5.677110    0.709469

    11.293017    0.207976

    6.590043    1.353117

    4.711960    0.194167

    8.768099    1.108041

    11.502519    0.545097

    4.682812    0.578112

    12.446578    0.300754

    12.908384    1.657722

    12.601108    0.974527

    3.929456    0.025466

    9.751503    1.182050

    3.043767    0.888168

    4.391522    0.807100

    11.695276    0.679015

    7.879742    0.154263

    5.613163    0.933632

    9.140172    0.851300

    4.258644    0.206892

    6.799831    1.221171

    8.752758    0.484418

    1.123033    1.180352

    10.833248    1.585426

    3.051618    0.026781

    5.308409    0.030683

    1.841792    0.028099

    2.261978    1.605603

    11.573696    1.061347

    8.038764    1.083910

    10.734007    0.103715

    9.661909    0.350772

    9.005850    0.548737

    0.000000    0.539131

    5.757140    1.062373

    9.164656    1.624565

    1.318340    1.436243

    14.075597    0.695934

    10.107550    1.308398

    7.960293    1.219760

    6.317292    0.018209

    12.664194    0.595653

    2.906644    0.581657

    2.388241    0.913938

    6.024471    0.486215

    7.226764    1.255329

    4.183997    1.275290

    11.850211    1.096981

    11.661797    1.167935

    3.574967    0.494666

    0.000000    0.107475

    7.937657    0.904799

    3.365027    1.014085

    0.000000    0.367491

    13.860672    1.293270

    10.306714    1.211594

    7.228002    0.670670

    4.508740    1.036192

    0.366328    0.163652

    3.299444    0.575152

    0.573287    0.607915

    9.183738    0.012280

    7.842646    1.060636

    4.750964    0.558240

    11.438702    1.556334

    8.243063    1.122768

    7.949017    0.271865

    7.875477    0.227085

    9.569087    0.364856

    7.750103    0.869094

    0.000000    1.515293

    3.396030    0.633977

    11.916091    0.025294

    0.460758    0.689586

    13.087566    0.476002

    4.589016    1.672600

    8.397217    1.534103

    5.562772    1.689388

    10.905159    0.619091

    1.311441    1.169887

    10.647170    0.980141

    0.000000    0.481918

    8.503025    0.830861

    0.436880    1.395314

    6.127867    1.102179

    12.112492    0.359680

    1.264968    1.141582

    6.067568    1.327047

    8.010964    1.681648

    3.791084    0.304072

    11.773195    1.262621

    8.339588    1.443357

    2.563092    1.464013

    5.954216    0.953782

    9.288374    0.767318

    3.976796    1.043109

    8.585227    1.455708

    1.271946    0.796506

    0.000000    0.242778

    0.000000    0.089749

    11.521298    0.300860

    1.139447    0.415373

    5.699090    1.391892

    2.449378    1.322560

    0.000000    1.228380

    3.168365    0.053993

    10.428610    1.126257

    2.943070    1.446816

    10.441348    0.975283

    12.478764    1.628726

    5.856902    0.363883

    2.476420    0.096075

    1.826637    0.811457

    4.324451    0.328235

    1.376085    1.178359

    5.342462    0.394527

    11.835521    0.693301

    12.423687    1.424264

    12.161273    0.071131

    8.148360    1.649194

    1.531067    1.549756

    3.200912    0.309679

    8.862691    0.530506

    6.370551    0.369350

    2.468841    0.145060

    11.054212    0.141508

    2.037080    0.715243

    13.364030    0.549972

    10.249135    0.192735

    10.464252    1.669767

    9.424574    0.013725

    4.458902    0.268444

    0.000000    0.575976

    9.686082    1.029808

    13.649402    1.052618

    13.181148    0.273014

    3.877472    0.401600

    1.413952    0.451380

    4.248986    1.430249

    8.779183    0.845947

    4.156252    0.097109

    5.580018    0.158401

    15.040440    1.366898

    12.793870    1.307323

    3.254877    0.669546

    10.725607    0.588588

    8.256473    0.765891

    8.033892    1.618562

    10.702532    0.204792

    5.062996    1.132555

    10.772286    0.668721

    1.892354    0.837028

    1.019966    0.372320

    15.546043    0.729742

    11.638205    0.409125

    3.427886    0.975616

    11.246174    1.475586

    0.000000    0.645045

    0.000000    1.424017

    8.242553    0.279069

    8.700060    0.101807

    0.812344    0.260334

    2.448235    1.176829

    13.230078    0.616147

    0.236133    0.340840

    11.155826    0.335131

    11.029636    0.505769

    2.901181    1.646633

    3.924594    1.143120

    2.524806    1.292848

    3.527474    1.449158

    3.384281    0.889268

    0.000000    1.107592

    11.898890    0.406441

    3.529892    1.375844

    11.442677    0.696919

    10.308145    0.422722

    8.540529    0.727373

    7.156949    1.691682

    0.720675    0.847574

    0.229405    1.038603

    3.399331    0.077501

    6.157239    0.580133

    1.239698    0.719989

    6.036854    0.016548

    5.258665    0.933722

    12.393001    1.571281

    9.627613    0.935842

    11.130453    0.597610

    8.842595    0.349768

    10.690010    1.456595

    5.714718    1.674780

    3.052505    1.335804

    0.000000    0.059025

    9.945307    1.287952

    2.719723    1.142148

    11.154055    1.608486

    2.687918    0.660836

    10.037847    0.962245

    12.404762    1.112080

    10.237305    0.633422

    4.745392    0.662520

    4.639461    1.569431

    3.149310    0.639669

    13.406875    1.639194

    6.068668    0.881241

    9.477022    0.899002

    3.897620    0.560201

    5.463615    1.203677

    3.369267    1.575043

    5.234562    0.825954

    0.000000    0.722170

    12.979069    0.504068

    5.376564    0.557476

    13.527910    1.586732

    2.196889    0.784587

    10.691748    0.007509

    1.659242    0.447066

    8.369667    0.656697

    13.157197    0.143248

    8.199667    0.908508

    4.441669    0.439381

    9.846492    0.644523

    0.019540    0.977949

    8.253774    0.748700

    6.038620    1.509646

    6.091587    1.694641

    8.986820    1.225165

    11.508473    1.624296

    8.807734    0.713922

    0.000000    0.816676

    8.889202    1.665414

    3.178117    0.542752

    7.013795    0.139909

    9.605014    0.065254

    1.230540    1.331674

    10.412811    0.890803

    0.000000    0.567161

    9.699991    0.122011

    0.000000    0.061191

    4.455293    0.272135

    3.020977    1.502803

    8.099278    0.216317

    1.157764    1.603217

    10.105396    0.121067

    11.230148    0.408603

    9.070058    0.011379

    0.566460    0.478837

    0.000000    0.487300

    8.956369    1.193484

    1.523057    0.620528

    2.749006    0.169855

    9.235393    0.188350

    10.555573    0.403927

    6.956372    1.519308

    0.636281    1.273984

    3.574737    0.075163

    9.032486    1.461809

    5.958993    0.023012

    2.435300    1.211744

    10.539731    1.638248

    7.646702    0.056513

    20.919349    0.644571

    1.424726    0.838447

    6.748663    0.890223

    2.289167    0.114881

    5.548377    0.402238

    6.057227    0.432666

    10.828595    0.559955

    11.318160    0.271094

    13.265311    0.633903

    0.000000    1.496715

    6.517133    0.402519

    4.934374    1.520028

    10.151738    0.896433

    2.425781    1.559467

    9.778962    1.195498

    12.219950    0.657677

    7.394151    0.954434

    8.518535    0.742546

    2.798700    0.662632

    0.637930    0.617373

    10.750490    0.097415

    0.625382    0.140969

    10.027968    0.282787

    9.817347    0.364197

    0.646828    1.266069

    3.347111    0.914294

    11.816892    0.193798

    0.000000    1.480198

    10.945666    0.993219

    10.244706    0.280539

    2.579801    1.149172

    2.630410    0.098869

    11.746200    1.695517

    8.104232    1.326277

    12.409743    0.790295

    12.167844    1.328086

    3.198408    0.299287

    16.055513    0.541052

    7.138659    0.158481

    4.831041    0.761419

    10.082890    1.373611

    10.066867    0.788470

    8.129538    0.329913

    3.012463    1.138108

    3.720391    0.845974

    0.773493    1.148256

    10.962941    1.037324

    0.177621    0.162614

    3.085853    0.967899

    8.426781    0.202558

    1.825927    1.128347

    2.185155    1.010173

    7.184595    1.261338

    0.000000    0.116525

    8.901752    1.033527

    2.451497    1.358795

    3.213631    0.432044

    3.974739    0.723929

    9.601306    0.619232

    8.363897    0.445341

    6.381484    1.365019

    0.000000    1.403914

    9.609836    1.438105

    9.904741    0.985862

    7.185807    1.489102

    5.466703    1.216571

    0.000000    0.915898

    4.575443    0.535671

    3.277076    1.010868

    10.246623    1.239634

    2.341735    1.060235

    3.201046    0.498843

    6.066013    0.120927

    8.829379    0.895657

    15.833048    1.568245

    13.516711    1.220153

    0.664284    1.116755

    6.325139    0.605109

    8.677499    0.344373

    8.188005    0.964896

    9.414263    0.384030

    9.196547    1.138253

    10.202968    0.452363

    2.119439    1.481661

    13.635078    0.858314

    0.083443    0.701669

    9.149096    1.051446

    1.933803    1.374388

    14.115544    0.676198

    8.933736    0.943352

    2.661254    0.946117

    0.988432    1.305027

    2.063741    1.125946

    2.220590    0.690754

    6.424849    0.806641

    1.156153    1.613674

    3.032720    0.601847

    3.076828    0.952089

    0.000000    0.318105

    7.750480    0.554015

    10.958135    1.482500

    10.222018    0.488678

    2.367988    0.435741

    7.686054    1.381455

    11.464879    1.481589

    11.075735    0.089726

    3.543989    0.345853

    8.123889    1.282880

    4.331769    0.754467

    0.120865    1.211961

    6.116109    0.701523

    7.474534    0.505790

    8.819454    0.649292

    6.802144    0.615284

    12.666325    0.931960

    8.636180    0.399333

    11.730991    1.289833

    8.132449    0.039062

    10.296589    1.496144

    7.583906    1.005764

    9.777806    0.496377

    8.833546    0.513876

    4.907899    1.518036

    8.362736    1.285939

    9.084726    1.606312

    14.164141    0.560970

    9.080683    0.989920

    6.522767    0.038548

    3.690342    0.462281

    3.563706    0.242019

    1.065870    1.141569

    6.683796    1.456317

    1.712874    0.243945

    13.109929    1.280111

    11.327910    0.780977

    4.545711    1.233254

    3.367889    0.468104

    8.326224    0.567347

    8.978339    1.442034

    5.655826    1.582159

    8.855312    0.570684

    6.649568    0.544233

    3.966325    0.850410

    1.924045    1.664782

    6.004812    0.280369

    0.000000    0.375849

    9.923018    0.092192

    2.389084    0.119284

    13.663189    0.133251

    11.434976    0.321216

    0.358270    1.292858

    9.598873    0.223524

    6.375275    0.608040

    11.580532    0.458401

    5.319324    1.598070

    4.324031    1.603481

    2.358370    1.273204

    0.000000    1.182708

    12.824376    0.890411

    1.587247    1.456982

    8.510324    1.520683

    10.428884    1.187734

    8.346618    0.042318

    7.541444    0.809226

    2.540946    1.583286

    9.473047    0.692513

    0.352284    0.474080

    0.000000    0.589826

    12.405171    0.567201

    4.126775    0.871452

    0.034087    0.335848

    1.177634    0.075106

    0.000000    0.479996

    0.994909    0.611135

    11.053664    1.180117

    0.000000    1.679729

    2.495011    1.459589

    11.516831    0.001156

    9.213215    0.797743

    5.332865    0.109288

    0.000000    1.689771

    0.000000    1.126053

    12.640062    1.690903

    2.693142    1.317518

    3.328969    0.268271

    7.193166    1.117456

    6.615512    1.521012

    8.000567    0.835341

    4.017541    0.512104

    13.245859    0.927465

    5.970616    0.813624

    11.668719    0.886902

    4.283237    1.272728

    10.742963    0.971401

    12.326672    1.592608

    0.000000    0.344622

    0.000000    0.922846

    10.602095    0.573686

    10.861859    1.155054

    1.229094    1.638690

    0.410392    1.313401

    14.552711    0.616162

    14.178043    0.616313

    14.136260    0.362388

    0.093534    1.207194

    10.929021    0.403110

    11.432919    0.825959

    9.134527    0.586846

    5.071432    1.421420

    11.460254    1.541749

    11.620039    1.103553

    4.022079    0.207307

    3.057842    1.631262

    7.782169    0.404385

    7.981741    0.929789

    4.601363    0.268326

    2.595564    1.115375

    10.049077    0.391045

    3.265444    1.572970

    11.780282    1.511014

    3.075975    0.286284

    1.795307    0.194343

    11.106979    0.202415

    5.994413    0.800021

    9.706062    1.012182

    10.582992    0.836025

    7.038266    1.458979

    0.023771    0.015314

    12.823982    0.676371

    3.617770    0.493483

    8.346684    0.253317

    6.104317    0.099207

    16.207776    0.584973

    6.401969    1.691873

    2.298696    0.559757

    7.661515    0.055981

    6.353608    1.645301

    10.442780    0.335870

    3.834509    1.346121

    10.998587    0.584555

    2.695935    1.512111

    3.356646    0.324230

    14.677836    0.793183

    1.551934    0.130902

    2.464739    0.223502

    1.533216    1.007481

    12.473921    0.162910

    6.491596    0.032576

    10.506276    1.510747

    4.380388    0.748506

    13.670988    1.687944

    8.317599    0.390409

    0.000000    0.556245

    0.000000    0.290218

    10.095799    1.188148

    0.860695    1.482632

    1.557564    0.711278

    10.072779    0.756030

    0.000000    0.431468

    7.140817    0.883813

    11.384548    1.438307

    3.214568    1.083536

    11.720655    0.301636

    6.374475    1.475925

    5.749684    0.198875

    3.871808    0.552602

    8.336309    0.636238

    9.710442    1.503735

    1.532611    1.433898

    9.785785    0.984614

    2.633627    1.097866

    9.238935    0.494701

    1.205656    1.398803

    3.124909    1.670121

    7.935489    1.585044

    12.746636    1.560352

    10.732563    0.545321

    3.977403    0.766103

    4.194426    0.450663

    9.610286    0.142912

    4.797555    1.260455

    1.615279    0.093002

    4.614771    1.027105

    0.000000    1.369726

    0.608457    0.512220

    6.558239    0.667579

    12.315116    0.197068

    7.014973    1.494616

    8.822304    1.194177

    10.086796    0.570455

    7.241614    1.661627

    4.602395    1.511768

    7.434921    0.079792

    10.467570    1.595418

    9.948127    0.003663

    2.478529    1.568987

    5.938545    0.878540

    0.000000    0.948004

    5.559181    1.357926

    9.776654    0.535966

    3.092056    0.490906

    0.000000    1.623311

    4.459495    0.538867

    8.334306    1.646600

    11.226654    0.384686

    3.904737    1.597294

    7.038205    1.211329

    9.836120    1.054340

    1.990976    0.378081

    9.005302    0.485385

    1.772510    1.039873

    0.458674    0.819560

    10.003919    0.231658

    0.520807    1.476008

    10.678214    1.431837

    4.425992    1.363842

    12.035355    0.831222

    10.606732    1.253858

    1.568653    0.684264

    2.545434    0.024271

    10.264062    0.982593

    9.866276    0.685218

    0.142704    0.057455

    9.853270    1.521432

    6.596604    1.653574

    2.602287    1.321481

    10.411776    0.664168

    7.083449    0.622589

    2.080068    1.254441

    0.522844    1.622458

    10.362000    1.544827

    3.412967    1.035410

    6.796548    1.112153

    4.092035    0.075804

    2.763811    1.564325

    12.547439    1.402443

    5.708052    1.596152

    4.558025    0.375806

    11.642307    0.438553

    3.222443    0.121399

    4.736156    0.029871

    10.839526    0.836323

    4.194791    0.235483

    14.936259    0.888582

    3.310699    1.521855

    2.971931    0.034321

    9.261667    0.537807

    7.791833    1.111416

    1.480470    1.028750

    3.677287    0.244167

    2.202967    1.370399

    5.796735    0.935893

    3.063333    0.144089

    11.233094    0.492487

    1.965570    0.005697

    8.616719    0.137419

    6.609989    1.083505

    1.712639    1.086297

    10.117445    1.299319

    0.000000    1.104178

    9.824777    1.346821

    1.653089    0.980949

    18.178822    1.473671

    6.781126    0.885340

    8.206750    1.549223

    10.081853    1.376745

    6.288742    0.112799

    3.695937    1.543589

    6.726151    1.069380

    12.969999    1.568223

    2.661390    1.531933

    7.072764    1.117386

    9.123366    1.318988

    3.743946    1.039546

    2.341300    0.219361

    0.541913    0.592348

    2.310828    1.436753

    6.226597    1.427316

    7.277876    0.489252

    0.000000    0.389459

    7.218221    1.098828

    8.777129    1.111464

    2.813428    0.819419

    2.268766    1.412130

    6.283627    0.571292

    7.520081    1.626868

    11.739225    0.027138

    3.746883    0.877350

    12.089835    0.521631

    12.310404    0.259339

    0.000000    0.671355

    2.728800    0.331502

    10.814342    0.607652

    12.170268    0.844205

    6.698371    0.240084

    3.632672    1.643479

    10.059991    0.892361

    1.887674    0.756162

    8.229125    0.195886

    7.817082    0.476102

    12.277230    0.076805

    10.055337    1.115778

    3.596002    1.485952

    2.755530    1.420655

    7.780991    0.513048

    0.093705    0.391834

    8.481567    0.520078

    3.865584    0.110062

    9.683709    0.779984

    10.617255    1.359970

    7.203216    1.624762

    7.601414    1.215605

    1.386107    1.417070

    9.129253    0.594089

    1.363447    0.620841

    3.181399    0.359329

    13.365414    0.217011

    4.207717    1.289767

    4.088395    0.870075

    3.327371    1.142505

    1.303323    1.235650

    7.999279    1.581763

    2.217488    0.864536

    7.751808    0.192451

    14.149305    1.591532

    8.765721    0.152808

    3.408996    0.184896

    1.251021    0.112340

    6.160619    1.537165

    1.034538    1.585162

    0.000000    1.034635

    2.355051    0.542603

    6.614543    0.153771

    10.245062    1.450903

    3.467074    1.231019

    7.487678    1.572293

    4.624115    1.185192

    8.995957    1.436479

    11.564476    0.007195

    3.440948    0.078331

    1.673603    0.732746

    4.719341    0.699755

    10.304798    1.576488

    2.086915    1.199312

    6.338220    1.131305

    8.254926    0.710694

    16.067108    0.974142

    1.723201    0.310488

    3.785045    0.876904

    2.557561    0.123738

    9.852220    1.095171

    3.679147    1.557205

    9.789681    0.852971

    14.958998    0.526707

    11.182148    1.288459

    7.528533    1.657487

    5.253802    1.378603

    13.946752    1.426657

    15.557263    1.430029

    12.483550    0.688513

    2.317302    1.411137

    10.069724    0.766119

    5.792231    1.615483

    4.138435    0.475994

    12.929517    0.304378

    9.378238    0.307392

    8.361362    1.643204

    7.939406    1.325042

    10.735384    0.705788

    11.592723    0.286188

    10.098356    0.704748

    9.299025    0.545337

    11.158297    0.218067

    16.143900    0.558388

    10.971700    1.221787

    0.000000    0.681478

    3.178961    1.292692

    17.625350    0.339926

    1.995833    0.267826

    10.640467    0.416181

    9.628339    0.985462

    4.662664    0.495403

    5.754047    1.382742

    0.000000    0.037146

    9.334332    0.198118

    3.846162    0.619968

    10.685084    0.678179

    4.752134    0.359205

    0.697630    0.966786

    10.365836    0.505898

    0.461478    0.352865

    11.339537    1.068740

    5.420280    0.127310

    3.469955    1.619947

    8.517067    0.994858

    8.306512    0.413690

    2.628690    0.444320

    0.000000    0.802985

    0.000000    1.170397

    7.298767    1.582346

    7.331319    1.277988

    9.392269    0.151617

    5.541201    1.180596

    15.149460    0.537540

    5.515189    0.250562

    7.728898    0.920494

    11.318785    1.510979

    3.574709    1.531514

    7.350965    0.026332

    7.122363    1.630177

    1.828412    1.013702

    10.117989    1.156862

    11.309897    0.086291

    8.342034    1.388569

    0.241714    0.715577

    10.482619    1.694972

    9.289510    1.428879

    4.269419    0.134181

    0.000000    0.189456

    0.817119    0.143668

    1.508394    0.652651

    9.359918    0.052262

    10.052333    0.550423

    11.111660    0.989159

    11.265971    0.724054

    10.383830    0.254836

    3.878569    1.377983

    13.679237    0.025346

    10.526846    0.781569

    0.000000    0.924198

    4.106727    1.085669

    8.118856    1.470686

    7.796874    0.052336

    2.789669    1.093070

    6.226962    0.287251

    10.169548    1.660104

    0.000000    1.370549

    7.513353    0.137348

    8.240793    0.099735

    14.612797    1.247390

    3.562976    0.445386

    3.230482    1.331698

    3.612548    1.551911

    0.000000    0.332365

    3.931299    0.487577

    14.752342    1.155160

    10.261887    1.628085

    2.787266    1.570402

    15.112319    1.324132

    5.184553    0.223382

    3.868359    0.128078

    3.507965    0.028904

    11.019254    0.427554

    3.812387    0.655245

    11.056784    0.378725

    8.826880    1.002328

    11.173861    1.478244

    11.506465    0.421993

    7.798138    0.147917

    10.155081    1.370039

    10.645275    0.693453

    9.663200    1.521541

    10.790404    1.312679

    2.810534    0.219962

    9.825999    1.388500

    1.421316    0.677603

    11.123219    0.809107

    13.402206    0.661524

    1.212255    0.836807

    1.568446    1.297469

    3.343473    1.312266

    5.400155    0.193494

    3.818754    0.590905

    7.973845    0.307364

    9.078824    0.734876

    0.153467    0.766619

    8.325167    0.028479

    7.092089    1.216733

    5.192485    1.094409

    10.340791    1.087721

    2.077169    1.019775

    10.151966    0.993105

    0.046826    0.809614

    11.221874    1.395015

    14.497963    1.019254

    3.554508    0.533462

    3.522673    0.086725

    14.531655    0.380172

    3.027528    0.885457

    1.845967    0.488985

    10.226164    0.804403

    10.965926    1.212328

    2.129921    1.477378

    0.000000    1.606849

    9.489005    0.827814

    0.000000    1.020797

    0.000000    1.270167

    6.556676    0.055183

    9.959588    0.060020

    7.436056    1.479856

    0.404888    0.459517

    9.952942    1.650279

    15.600252    0.021935

    2.723846    0.387455

    0.513866    1.323448

    0.000000    0.861859

    7.280602    1.438470

    9.161978    1.110180

    0.991725    0.730979

    7.398380    0.684218

    12.149747    1.389088

    9.149678    0.874905

    9.666576    1.370330

    3.620110    0.287767

    5.238800    1.253646

    14.715782    1.503758

    14.445740    1.211160

    13.609528    0.364240

    3.141585    0.424280

    0.000000    0.120947

    0.454750    1.033280

    0.510310    0.016395

    3.864171    0.616349

    6.724021    0.563044

    4.289375    0.012563

    0.000000    1.437030

    3.733617    0.698269

    2.002589    1.380184

    2.502627    0.184223

    6.382129    0.876581

    8.546741    0.128706

    2.694977    0.432818

    3.951256    0.333300

    9.856183    0.329181

    2.068962    0.429927

    3.410627    0.631838

    9.974715    0.669787

    10.650102    0.866627

    9.134528    0.728045

    7.882601    1.332446

data.txt

代码:

import numpy as np

import operator

import matplotlib.pyplot as plt

def knn_classifier(inX, train_data, labels, k):

    """

    Knn_Classifier k近邻核心实现代码

    :param inX: 输入待测试实例

    :param train_data: 输入的训练数据集

    :param labels: 训练数据集对应的标签

    :param k: 分为k类

    :return: 返回对应的类别

    """

    train_data_size = train_data.shape[0]  # 获取数据集的

    diff_matrix = np.tile(inX, (train_data_size, 1)) - train_data  # 计算inx与训练数据集中所有数据的差值

    lp_diff_matrix = diff_matrix**2  # 这里采用的是欧氏距离

    lp_distances = lp_diff_matrix.sum(axis=1)

    distances = lp_distances**0.5

    sorted_dist_indicies = np.argsort(distances)  # 按照欧氏距离的大小进行排序

    class_count = {}

    for i in range(k):

        vote_I_label = labels[sorted_dist_indicies[i]]  # 依次存入欧氏距离前k个最小距离的编号

        class_count[vote_I_label] = class_count.get(vote_I_label, 0) + 1  # 对应一个字典

    sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)  # 对字典进行排序

    return sorted_class_count[0][0]  # 最高值对应类别即为inX的类别

def file_to_matrix(filename):

    '''

    文件数据转换为矩阵类型

    :param filename:

    :return:

    '''

    f = open(filename)

    lines = f.readlines()

    lines_number = len(lines)

    feature = len(lines[1].split('\t'))

    matrix = np.zeros((lines_number, feature - 1))

    class_label_vector = []

    index = 0

    for line in lines:

        line = line.strip()

        item = line.split('\t')

        matrix[index, :] = item[0:3]

        class_label_vector.append(item[-1])

        index += 1

    return matrix, class_label_vector

def auto_norm(data_set):

    """

    auto_norm 归一化函数，消除量纲不同，不同属性的大小差异过大的影响

    归一化公式 newValue = (oldValue - min)/(max - min)  取值0-1

    :param dataSet:

    :return:

    """

    min_vals = data_set.min(0)

    max_vals = data_set.max(0)

    ranges = max_vals - min_vals

    # print(type(min_vals))

    m = data_set.shape[0]

    data_set = data_set - np.tile(min_vals, (m, 1))

    data_set = data_set/(np.tile(ranges, (m, 1)))

    return data_set, ranges, min_vals

def dating_class_test():

    """

    dating_class_test 测试约会数据集data2的聚类预测结果

    return: null

    """

    ho_ratio = 0.1

    dating_matrix, dating_labels = file_to_matrix('data2.txt')  # 读入数据

    norm_matrix, ranges, min_vals = auto_norm(dating_matrix)  # 归一化数据

    m = norm_matrix.shape[0]  # 获取行数

    num_test_vecs = int(m * ho_ratio)  # 取出其中的10%作为测试数据

    error_count = 0.0  # 记录错误率

    for i in range(num_test_vecs):

        classifier = knn_classifier(norm_matrix[i, :], norm_matrix[num_test_vecs:m, :], dating_labels[num_test_vecs:m], 4)  #利用KNN聚类算法进行预测

        print("the classifier came back with: " +classifier + " the real answer is: " + dating_labels[i])

        if(classifier != dating_labels[i]) :

            error_count += 1.0

    print('the total error rate is: %f' % (error_count/float(num_test_vecs)))

if __name__ == "__main__":

    dating_class_test()