C/C++二叉树搜索树操作集

啥是二叉查找树

在数据结构中，有一个奇葩的东西，说它奇葩，那是因为它重要，这就是树。而在树中，二叉树又是当中的贵族。二叉树的一个重要应用是它们在查找中的应用，于是就有了二叉查找树。 使二叉树成为一颗二叉查找树，需要满足以下两点：

1. 对于树中的每个节点X，它的左子树中所有项的值都要小于X中的项；
2. 对于树中的每个节点Y，它的右子树中所有项的值都要大于Y中的项。

二叉查找树的基本操作

以下是对于二叉查找树的基本操作定义类，然后慢慢分析是如何实现它们的。

template<class T>
class BinarySearchTree
{
public:
    // 构造函数，初始化root值
    BinarySearchTree() : root(NULL){}

    // 析构函数，默认实现
    ~BinarySearchTree() {}

    // 查找最小值，并返回最小值
    const T &findMin() const;

    // 查找最大值，并返回最大值
    const T &findMax() const;

    // 判断二叉树中是否包含指定值的元素
    bool contains(const T &x) const;

    // 判断二叉查找树是否为空
    bool isEmpty() const { return root ? false : true; }

    // 打印二叉查找树的值
    void printTree() const;

    // 向二叉查找树中插入指定值
    void insert(const T &x);

    // 删除二叉查找树中指定的值
    void remove(const T &x);

    // 清空整个二叉查找树
    void makeEmpty() const;

private:
    // 指向根节点
    BinaryNode<T> *root;

    void insert(const T &x, BinaryNode<T> *&t) const;
    void remove(const T &x, BinaryNode<T> *&t) const;
    BinaryNode<T> *findMin(BinaryNode<T> *t) const;
    BinaryNode<T> *findMax(BinaryNode<T> *t) const;
    bool contains(const T &x, BinaryNode<T> *t) const;
    void printTree(BinaryNode<T> *t) const;
    void makeEmpty(BinaryNode<T> *&t) const;
};

findMin和findMax实现

根据二叉查找树的性质：

1. 对于树中的每个节点X，它的左子树中所有项的值都要小于X中的项；
2. 对于树中的每个节点Y，它的右子树中所有项的值都要大于Y中的项。

我们可以从root节点开始：

1. 一直沿着左节点往下找，直到子节点等于NULL为止，这样就可以找到最小值了；
2. 一直沿着右节点往下找，直到子节点等于NULL为止，这样就可以找到最大值了。

如下图所示：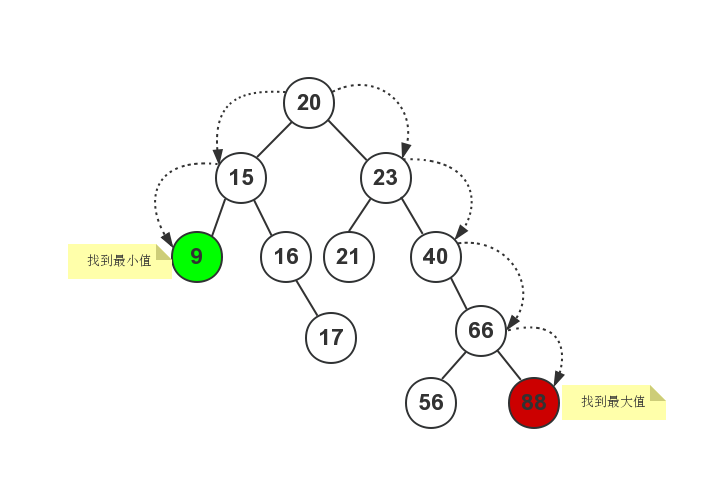 

在程序中实现时，有两种方法：

1. 使用递归实现；
2. 使用非递归的方式实现。

对于finMin的实现，我这里使用递归的方式，代码参考如下：

BinaryNode<T> *BinarySearchTree<T>::findMin(BinaryNode<T> *t) const
{
    if (t == NULL)
    {
        return NULL;
    }
    else if (t->left == NULL)
    {
        return t;
    }
    else
    {
        return findMin(t->left);
    }
}

在findMin()的内部调用findMin(BinaryNode<T> *t)，这样就防止了客户端知道了root根节点的信息。上面使用递归的方式实现了查找最小值，下面使用循环的方式来实现findMax。

template<class T>
BinaryNode<T> *BinarySearchTree<T>::findMax(BinaryNode<T> *t) const
{
    if (t == NULL)
    {
        return NULL;
    }

    while (t->right)
    {
        t = t->right;
    }
    return t;
}

在很多面试的场合下，面试官一般都是让写出非递归的版本；而在对树进行的各种操作，很多时候都是使用的递归实现的，所以，在平时学习时，在理解递归版本的前提下，需要关心一下对应的非递归版本。

contains实现

contains用来判断二叉查找树是否包含指定的元素。代码实现如下：

template<class T>
bool BinarySearchTree<T>::contains(const T &x, BinaryNode<T> *t) const
{
    if (t == NULL)
    {
        return false;
    }
    else if (x > t->element)
    {
        return contains(x, t->right);
    }
    else if (x < t->element)
    {
        return contains(x, t->left);
    }
    else
    {
        return true;
    }
}

算法规则如下：

1. 首先判断需要查找的值与当前节点值的大小关系；
2. 当小于当前节点值时，就在左节点中继续查找；
3. 当大于当前节点值时，就在右节点中继续查找；
4. 当找到该值时，直接返回true。

insert实现

insert函数用来向二叉查找树中插入新的元素，算法处理如下：

1. 首先判断需要插入的值与当前节点值得大小关系；
2. 当小于当前节点值时，就在左节点中继续查找插入点；
3. 当大于当前节点值时，就在右节点中继续查找插入点；
4. 当等于当前节点值时，什么也不干。

代码实现如下：

template<class T>
void BinarySearchTree<T>::insert(const T &x, BinaryNode<T> *&t) const
{
    if (t == NULL)
    {
        t = new BinaryNode<T>(x, NULL, NULL);
    }
    else if (x < t->element)
    {
        insert(x, t->left);
    }
    else if (x > t->element)
    {
        insert(x, t->right);
    }
}

remove实现

remove函数用来删除二叉查找树中指定的元素值，这个处理起来比较麻烦。在删除子节点时，需要分以下几种情况进行考虑（结合下图进行说明）： 如下图所示：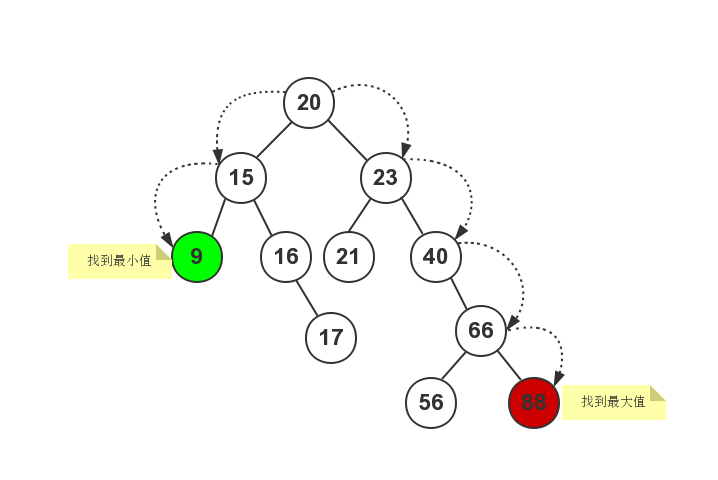 

1. 需要删除的子节点，它没有任何子节点；例如图中的节点9、节点17、节点21、节点56和节点88；这些节点它们都没有子节点；
2. 需要删除的子节点，只有一个子节点（只有左子节点或右子节点）；例如图中的节点16和节点40；这些节点它们都只有一个子节点；
3. 需要删除的子节点，同时拥有两个子节点；例如图中的节点66等。

对于情况1，直接删除对应的节点即可；实现起来时比较简单的；

对于情况2，直接删除对应的节点，然后用其子节点占据删除掉的位置；

对于情况3，是比较复杂的。首先在需要被删除节点的右子树中找到最小值节点，然后使用该最小值替换需要删除节点的值，然后在右子树中删除该最小值节点。
假如现在需要删除包含值23的节点，步骤如下图所示：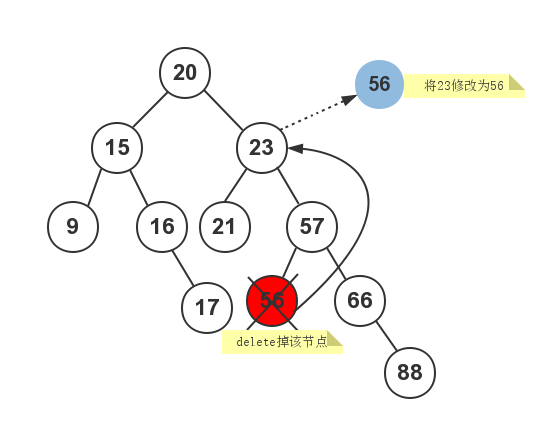 

代码实现如下：

template<class T>
void BinarySearchTree<T>::remove(const T &x, BinaryNode<T> *&t) const
{
    if (t == NULL)
    {
        return;
    }

    if (x < t->element)
    {
        remove(x, t->left);
    }
    else if (x > t->element)
    {
        remove(x, t->right);
    }
    else if (t->left != NULL && t->right != NULL)
    {
        // 拥有两个子节点
        t->element = findMin(t->right)->element;
        remove(t->element, t->right);
    }
    else if (t->left == NULL && t->right == NULL)
    {
        // 没有子节点，直接干掉
        delete t;
        t = NULL;
    }
    else if (t->left == NULL || t->right == NULL)
    {
        // 拥有一个子节点
        BinaryNode *pTemp = t;
        t = (t->left != NULL) ? t->left : t->right;
        delete pTemp;
    }
}

makeEmpty实现

makeEmpty函数用来释放整个二叉查找树占用的内存空间，同理，也是使用的递归的方式来实现的。具体代码请下载文中最后提供的源码。

转载：http://www.jellythink.com/archives/692

@2017-03-29 20:25:17 测试通过：

/*!
 * \file 二叉搜索树的实现.cpp
 *
 * \author ranjiewen
 * \date 2017/03/29 17:13
 *
 *
 */

#include <stdio.h>
#include <stdlib.h>

typedef int ELementType;
typedef struct BSTreeNode* BSTree;

struct BSTreeNode  //不可以typedef;然后再次typedef;
{
    ELementType Data;
    BSTree Left;
    BSTree Right;
};

//typedef BSTreeNode* Position;
typedef BSTree Position;

Position Find(ELementType x, BSTree BST); //返回所在节点的地址
Position FindMin(BSTree BST);
Position FinMax(BSTree BST);
BSTree Insert(ELementType x, BSTree BST);
BSTree Delete(ELementType x, BSTree BST);

//查找的效率取决于树的高度，和树的组织方法有关
Position Find(ELementType x, BSTree BST)
{
    if (!BST)
    {
        return NULL;
    }
    if (x > BST->Data)
    {
        return Find(x, BST->Right);  //尾递归都可以用循环的实现
    }
    else if (x < BST->Data)
    {
        return Find(x, BST->Left);
    }
    else  //x==BST->Data
    {
        return BST;
    }
}

//非递归的执行效率高，可将“尾递归”函数改为迭代函数实现
Position IterFinde(ELementType x, BSTree BST)
{
    while (BST)
    {
        if (x > BST->Data)
        {
            BST = BST->Right;
        }
        else if (x < BST->Data)
        {
            BST = BST->Left;
        }
        else
        {
            return BST;
        }
    }
    return NULL;
}

//递归实现
Position FindMin(BSTree BST)
{
    if (!BST)
    {
        return NULL;
    }
    else if (!BST->Left)
    {
        return BST;    //找到最左叶节点并返回
    }
    else
    {
        return FindMin(BST->Left);
    }
}

Position FinMax(BSTree    BST)
{
    if (!BST)
    {
        return NULL;
    }
    while (BST->Right)
    {
        BST = BST->Right;  //沿右分支继续查找，直到最右节点
    }
    return BST;
}

//关键是要找到元素应该插入的位置，可以采用与Find类似的方法
BSTree Insert(ELementType x, BSTree BST)
{
    if (!BST)
    {
        BST = (BSTree)malloc(sizeof(BSTreeNode));
        BST->Data = x;
        BST->Left = NULL;
        BST->Right = NULL;
    }
    else  //开始找到要插入元素的位置
    {
        if (x < BST->Data)
        {
            BST->Left = Insert(x, BST->Left);  //将子树的根节点挂在父节点下
        }
        else if (x > BST->Data)
        {
            BST->Right = Insert(x, BST->Right);
        }
        //else x已经存在
    }
    return BST;
}

//删除节点的三种情况：
//     1.要删除的是叶节点：直接删除，并修改其父节点为NULL
//     2.要删除的结点只有一个孩子结点: 将其父结点的指针指向要删除结点的孩子结点
//     3.要删除的结点有左、右两棵子树： 用另一结点替代被删除结点：右子树的最小元素 或者 左子树的最大元素

BSTree Delete(ELementType x, BSTree BST)
{
    Position temp;
    if (!BST)
    {
        printf("要删除的元素未找到...\n");
    }
    else if (x < BST->Data)
    {
        BST->Left = Delete(x, BST->Left);
    }
    else if (x > BST->Data)
    {
        BST->Right = Delete(x, BST->Right);
    }
    else  //找到要删除的节点
    {
        if (BST->Left&&BST->Right) /*被删除的节点有左右两个子节点*/
        {
            temp = FindMin(BST->Right);

            BST->Data = temp->Data;
            BST->Right = Delete(BST->Data, BST->Right);
        }
        else   //被删除节点有一个或者无子节点 //这里的理解：已经到尾节点了，只有一个元素了
        {
            temp = BST;
            if (!BST->Left) //有右孩子
            {
                BST = BST->Right;
            }
            else if (!BST->Right)
            {
                BST = BST->Left;
            }
            free(temp);
        }
    }
    return BST;
}

BSTree CreateBST(BSTree BST)
{
    int N = ;
    printf("请输入创建二叉搜索树的元素个数：\n");
    scanf("%d", &N);
    int data = ;
    for (int i = ; i < N; i++)
    {
        //scanf("%d", data);
        BST=Insert(i + , BST);//
    }
    return BST;
}

void PrintBST(BSTree BST)  //考虑怎么可视化的输出
{
    if (BST) //中序打印
    {
        PrintBST(BST->Left);
        printf("%3d", BST->Data);
        PrintBST(BST->Right);
    }
}

int main()
{
    BSTree root = NULL;
    //CreateBST(root);void 不行，要考虑怎么将节点传出来； 1.根据返回值   2.用传指针的方式，所有函数形参改为指针的指针&root

    root = CreateBST(root);
    PrintBST(root);
    printf("\n");

    BSTree temp;
    temp = Find(, root);
    if (temp)
    {
        printf("search success!,search data is %d.\n", temp->Data);
    }
    else
    {
        printf("search failed!\n");
    }

    temp = IterFinde(, root);
    if (temp)
    {
        printf("search success!,search data is %d.\n", temp->Data);
    }
    else
    {
        printf("search failed!\n");
    }

    root=Insert(, root);
    PrintBST(root);
    printf("\n");

    root=Delete(, root);
    PrintBST(root);
    printf("\n");

    return ;
}

补充：今天做了一个实验，感觉删除操作没有理解

#include <stdio.h>
#include <stdlib.h>

typedef struct node {
    int key;
    struct node *LChild, *RChild; //孩子指针
}BSTNode, *BSTree;   //定义二叉树----查找树

void CreatBST(BSTree *bst);
BSTree SearchBST(BSTree bst, int key);
void InsertBST(BSTree *bst, int key);
BSTNode * DelBST(BSTree t, int k);//以上是函数的声明

void print_bst(BSTree t) //打印
{
    if (t)//中序顺序打印
    {
        print_bst(t->LChild);
        printf("%d\t", t->key);
        print_bst(t->RChild);
    }
}
const int n = ;
/*创建树*/
void CreatBST(BSTree *bst)
{
    printf("请输入%d个数创建二叉搜索树：",n);
    int i;
    int key;
    *bst = NULL;
    for (i = ; i <= n; i++)
    {
        scanf("%d", &key);
        InsertBST(bst, key); //创建
    };
}
/*寻找*/
BSTree SearchBST(BSTree bst, int key)
{
    if (!bst)
        return nullptr;       //bst为空
    else   if (bst->key == key)
    {
        printf("查找成功！");
        return bst;           //找到，返回节点
    }
    else   if (key < bst->key)
        return SearchBST(bst->LChild, key); //左孩子递归调用查找
    else
        return SearchBST(bst->RChild, key); //右孩子递归
}
/*插入*/
void InsertBST(BSTree *bst, int key)
{
    BSTree t;
    if (*bst == NULL)
    {
        t = (BSTree)malloc(sizeof(BSTNode)); //树为空，申请空间
        t->key = key;
        t->LChild = NULL;
        t->RChild = NULL;
        *bst = t; //插入
        //printf("插入成功！");
    }
    else if (key <(*bst)->key)
        InsertBST(&((*bst)->LChild), key); //插到左子树
    else if (key>(*bst)->key)
        InsertBST(&((*bst)->RChild), key); //插到右子树
}
/*删除*/   //有问题？没有理解！
BSTNode * DelBST(BSTree t, int k)  //根据LR为0或1,删除T中p所指结点的左或右子树
{
    BSTNode *p, *f, *s, *q;
    p = t;
    s = t;//
    f = NULL;
    while (p) //树非空,先找到key的位置
    {
        if (p->key == k) //根节点等于K
            break;
        f = p;          //f记录k所在的节点的 双亲节点
        if (p->key > k) //向左子树方向
            p = p->LChild;
        else
            p = p->RChild; //右
    }
    if (p == NULL) //为空
        return t;
    if (p->LChild == nullptr)  //左空 ，下边就是删除过程
    {
        if (f == NULL)
            t = p->RChild;
        else if (f->LChild == p)
            f->LChild = p->RChild;
        else
            f->RChild = p->LChild;
        free(p); //释放空间
    }
    else //右，下边就是删除过程
    {
        q = p;
        s = s->LChild;
        while (s->RChild)
        {
            q = s;
            s = s->RChild;
        }
        if (q == p)
            q->LChild = s->LChild;
        else
            q->RChild = s->LChild;
        p->key = s->key;
        free(s); //释放空间
    }
    return t;
}

int main()
{
    BSTNode * root=nullptr;
    int loop, i, data;
    loop = true;
    while (loop)
    {
        printf("\n***************二叉树操作菜单**************\n");
        printf(" 1.创建\n");
        printf(" 2.查找\n");
        printf(" 3.插入\n");
        printf(" 4.删除\n");
        printf(" 5.打印\n");
        printf(" 0.退出\n");
        scanf("%d", &i);
        switch (i)
        {
        case :
        {
                  loop = false;
                  break;
        }
        case :
        {
                  CreatBST(&root);
        }break;
        case :
        {
                  printf("Please input the data you want search.\n");
                  scanf("%d", &data);
                  SearchBST(root, data);

        }break;
        case :
        {         printf("Please input the data you want insert.\n");
                  scanf("%d", &data);
                  InsertBST(&root, data);
                  printf("插入成功！");
        }break;
        case :
        {
                  printf("Please input the data you want delete.\n");
                  scanf("%d", &data);
                  root = DelBST(root, data);
        }break;
        case :{
                   printf("\n");
                   if (root != NULL)
                       printf("The BSTree's root is:%d\n", root->key);
                   print_bst(root);
                   break;
        }
        }
    }
}

//C++实现
#include <iostream>
#include <cstring>
using namespace std;

typedef int KeyType;
#define NUM 11

class BinStree;
class BinSTreeNode
{
public:
    KeyType key;
    BinSTreeNode *lchild;
    BinSTreeNode *rchild;
    BinSTreeNode()
    {
        lchild = NULL;
        rchild = NULL;
    }
};

class BinSTree
{
public:
    BinSTreeNode *root;
    BinSTree()
    {
        root = NULL;
    }
    ~BinSTree()
    {
        //delete root;
    }
    BinSTreeNode *BSTreeSearch(BinSTreeNode *bt, KeyType k, BinSTreeNode *&p);
    void BSTreeInsert(BinSTreeNode *&bt, KeyType k);
    int BSTreeDelete(BinSTreeNode *&bt, KeyType k);
    void BSTreePreOrder(BinSTreeNode *bt);
    bool IsEmpty()
    {
        return root == NULL;
    }
};

/**
*  二叉树排序查找算法
*  在根指针为bt的二叉排序树中查找元素k的节点，若查找成功，则返回指向该节点的指针
*  参数p指向查找到的结点，否则返回空指针，参数p指向k应插入的父结点
*/
BinSTreeNode* BinSTree::BSTreeSearch(BinSTreeNode *bt, KeyType k, BinSTreeNode *&p)
{
    BinSTreeNode *q = NULL;
    q = bt;
    while (q)
    {
        p = q;
        if (q->key == k)
        {
            return(p);
        }
        if (q->key > k)
            q = q->lchild;
        else
            q = q->rchild;
    }
    return NULL;
}

/**
*  二叉排序树的插入节点算法
*  bt指向二叉排序树的根结点，插入元素k的结点
*/
void BinSTree::BSTreeInsert(BinSTreeNode *&bt, KeyType k)
{
    BinSTreeNode *p = NULL, *q;
    q = bt;
    if (BSTreeSearch(q, k, p) == NULL)
    {
        BinSTreeNode *r = new BinSTreeNode;
        r->key = k;
        r->lchild = r->rchild = NULL;
        if (q == NULL)
        {
            bt = r;         //被插入节点做为树的根节点
        }
        if (p && k < p->key)
            p->lchild = r;
        else if (p)
            p->rchild = r;
    }
}
/**
* 先序遍历
*/
void BinSTree::BSTreePreOrder(BinSTreeNode *bt)
{
    if (bt != NULL)
    {
        cout << bt->key << " ";
        BSTreePreOrder(bt->lchild);
        BSTreePreOrder(bt->rchild);
    }
}
/**
* 二叉排序树的删除结点算法
* 在二叉排序树中删除元素为k的结点，*bt指向二叉排序树的根节点
* 删除成功返回1，不成功返回0.
*/
int BinSTree::BSTreeDelete(BinSTreeNode *&bt, KeyType k)
{
    BinSTreeNode *f, *p, *q, *s;
    p = bt;
    f = NULL;
    //查找关键字为k的结点，同时将此结点的双亲找出来
    while (p && p->key != k)
    {
        f = p;  //f为双亲
        if (p->key > k)
            p = p->lchild;
        else
            p = p->rchild;
    }
    if (p == NULL)   //找不到待删除的结点时返回
        return ;
    if (p->lchild == NULL)  //待删除结点的左子树为空
    {
        if (f == NULL)  //待删除结点为根节点
            bt = p->rchild;
        else if (f->lchild == p)  //待删结点是其双亲结点的左节点
            f->lchild = p->rchild;
        else
            f->rchild = p->rchild;  //待删结点是其双亲结点的右节点
        delete p;
    }
    else                    //待删除结点有左子树，相当于有二个节点
    {
        q = p;
        s = p->lchild;
        while (s->rchild)  //在待删除结点的左子树中查找最右下结点
        {
            q = s;
            s = s->rchild;  //找左子树的最大值
        }
        if (q == p)
            q->lchild = s->lchild;
        else
            q->rchild = s->lchild;

        p->key = s->key;
        delete s;
    }
    return ;
}
int main(void)
{
    int a[NUM] = { , , , , , , , , , ,  };
    int i;
    BinSTree bst;
    BinSTreeNode *pBt = NULL, *p = NULL, *pT = NULL;

    for (i = ; i < NUM; i++)
    {
        bst.BSTreeInsert(pBt, a[i]); //创建二叉排序树
    }
    pT = bst.BSTreeSearch(pBt, , p); //搜索排序二叉树
    bst.BSTreePreOrder(pBt);
    cout << endl;
    bst.BSTreeDelete(pBt, );   //删除无左孩子的情况
    bst.BSTreePreOrder(pBt);
    cout << endl;
    bst.BSTreeDelete(pBt, );   //删除有左孩子的情况
    bst.BSTreePreOrder(pBt);
    cout << endl;
    return ;
}

C++实现二叉查找树