CodeForces 757D Felicity's Big Secret Revealed（状压DP）

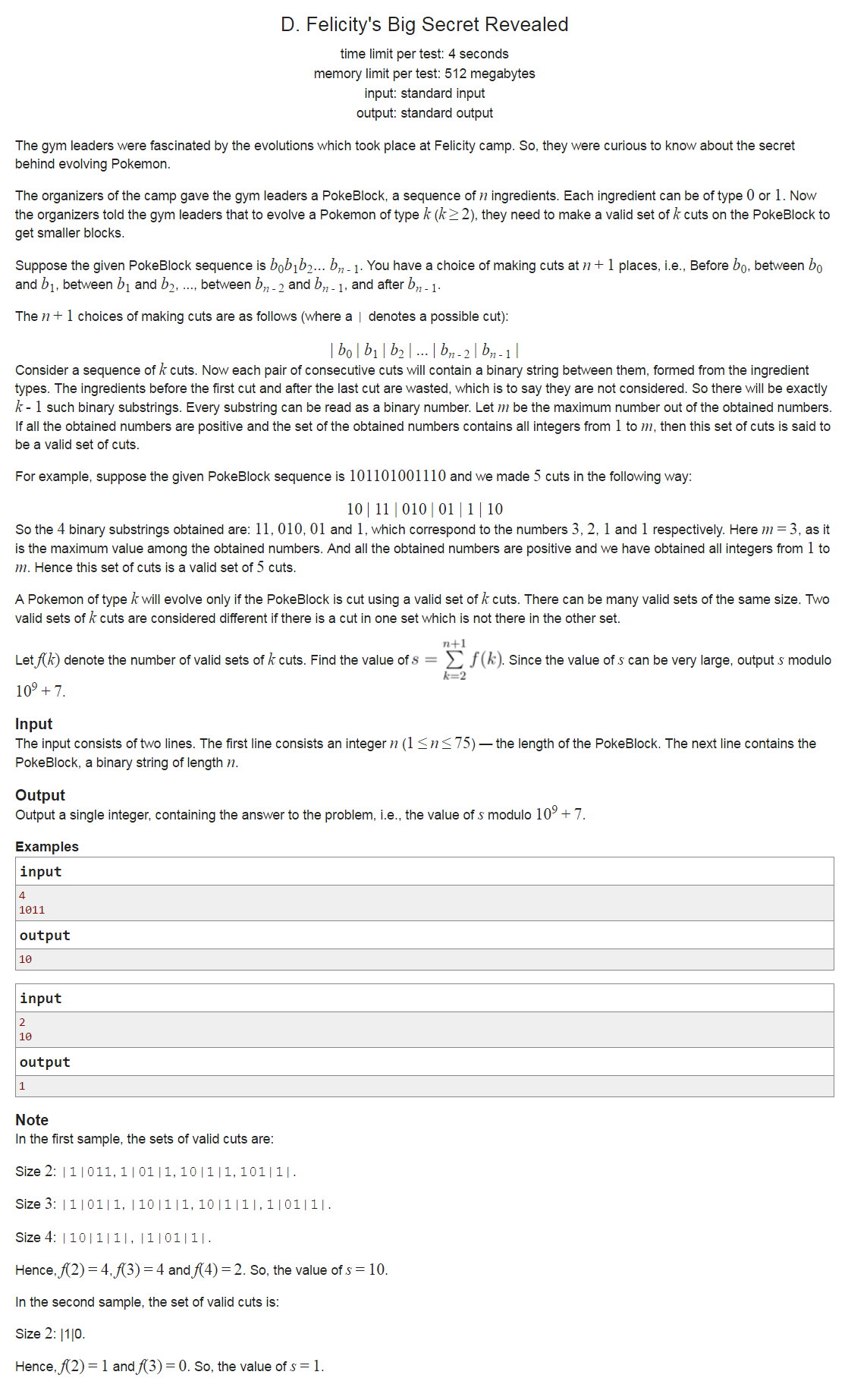
题意：给定一个01串，一个有效的n切割定义如下：一个横杠代表一次切割，第一条横杠前面的01串不算，最后一条横杠后面的01串不算，将两个横杠中的01串转化成十进制数字，假设这些数字的最大值是MAX且这些数字囊括了1-MAX的所有数字，则称为一次有效切割。求2~n+1次有效切割的切法。

思路: 由于题目要求包含所有1—MAXN的数字，且n<=75，所以MAXN<=20。另dp[i][j]表示第i位前面有一个横杆且存在j这个状态，接着从第i位开始枚举到第j位为下一个横杆的位置，设这两段横杆之间的数字为p（十进制），则递推式子为

dp[j+1][k|(1<<p-1)]+=dp[i][k]，k为1～（1<<20）的状态。最后把dp[i][(1<<t)-1]（0<=i<=n，1<=t<=20）加起来就可以了。

 #include <iostream>
 #include <queue>
 #include <stack>
 #include <cstdio>
 #include <vector>
 #include <map>
 #include <set>
 #include <bitset>
 #include <algorithm>
 #include <cmath>
 #include <cstring>
 #include <cstdlib>
 #include <string>
 #include <sstream>
 #include <time.h>
 #define x first
 #define y second
 #define pb push_back
 #define mp make_pair
 #define lson l,m,rt*2
 #define rson m+1,r,rt*2+1
 #define mt(A,B) memset(A,B,sizeof(A))
 #define mod 1000000007
 using namespace std;
 typedef long long LL;
 const double PI = acos(-);
 const int N=1e5+;
 const int inf = 0x3f3f3f3f;
 const LL INF=0x3f3f3f3f3f3f3f3fLL;
 int dp[][(<<)+];
 int a[];
 int main()
 {
 #ifdef Local
     freopen("data","r",stdin);
 #endif
      int n,p,ans=;
      cin>>n;
      mt(dp,);
      for(int i=;i<n;i++)scanf("%1d",&a[i]);
      for(int i=;i<n;i++)
      {
          dp[i][]=;
          for(int k=;k<(<<);k++)
          {
              if(!dp[i][k])continue;
              for(int j=i,p=a[i];j<n&&p<=;j++,p=((p<<)+a[j]))
              {
                  if(p)dp[j+][k|(<<p-)]=(dp[j+][k|(<<p-)]+dp[i][k])%mod;
              }
          }
      }
      for(int i=;i<=n;i++)
      {
          for(int k=;k<=;k++)
          {
             ans=(ans+dp[i][(<<k)-])%mod;
          }
      }
      cout<<ans<<endl;
 #ifdef Local
     cerr << "time: " << (LL) clock() *  / CLOCKS_PER_SEC << " ms" << endl;
 #endif
 }