最短路径Shortest Path algorithm

最短路径问题：

如果从图中某一顶点（称为端点）到达另一顶点（称为终点）的路径可能不止一条，如何找到一条路径使得沿此路径上各边上的权值总和达到最小。

（1）Dijkstra 算法 (2) Floyd 算法

1、边上权值非负情形的单源最短路径问题

为求得这些最短路径，Dijkstra提出按路径长度的递增次序，逐步产生最短路径的算法。首先求出长度最短的一条路径，在参照它求出长度次短的一条路径，以此类推，直到从顶点v到其他各顶点的最短路径全部求出为止。

1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

引入辅助数组dist。它的每一个分量dist[i]表示当前找到的从源点v0到终点vi的最短路径长度。

初始状态：

若从源点v0到顶点有边，则dist[i]为该边上的权值；

若从源点v0到顶点vi无边，则dist[i]为无穷。

2)算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

dtst[j]=Edge[0][j], j=1,2 ,..., n-1;

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

dist[k]=min{dist[i]}

c.修改以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

void ShortestPath(MTGraph G, int v)
{
	//MTGraph是一个n顶点的带权有向图
	EdgeData dist[G.n]; //最短路径长度数组
	int path[G.n];      //最短路径数组
	int S[G.n];      //最短路径顶点集合

	for（int i=0;i<n;i++)
    {
       dist[i]=G.Edge[v][i];   //dist 数组初始化
       S[i]=0;     //集合S初始化
       if(i!=v && dist[i]<MaxValue)
          path[i]=v;
       else path[i]=-1;     //path数组初始化
    }
    //顶点v加入顶点集合
    S[v]=1;
    dist[v]=0;

    //扩充集合S
    for(int i=0;i<n-1;i++)
    {
    	double min = MaxValue;
    	int u=v;
    	for(int j=0;j<n;j++)
    		if(!S[j] && dist[j] < min)
    		{
    			u=j;
    			min=dist[j];
    		}
    	S[u]=1;   //将顶点u加入集合S
    	for(int w=0;w<n;w++)   //修改
    		if(!S[w] && G.Edge[u][w] < MaxValue
    			&& dist[u]+G.Edge[u][w] < dist[w])
    		{
    			dist[w]=dist[u]+G.Edge[u][w];
    			path[w]=u;
    		}
    }

    //打印各顶点的最短路径：路径逆向输出
    for(int i=0;i<G.n;i++)
    {
    	cout<<endl;
    	cout<<"Distence:"<<dist[i]<<"Path:"<<i;

    	int pre = path[i];
    	while(pre!=v)
    	{
    		cout<<","<<pre;
    		pre=path[pre];
    	}
    }
}

　　

时间复杂度为O(n^2)

(2) Floyd-Warshall算法

算法思想：
对于顶点i和j:

首先：

考虑从i到j 是否有以顶点1为中间点的路径： i, 1, j, 即考虑图中是否有边<i, 1>和<1, j>，若有，则新路径i，1，j的长度是C[i][1]+C[1][j]，比较路径i, j和i,1,j的长度，并以较短者为当前所求得的最短路径。该路径是中间点序号不大于1的最短路径。

其次：

考虑，从i到j是否包含顶点2为中间点的路径，若没有，则从i到j 的最短路径任然是第一步中求出的，若有，则 i, ... , 2, ... , j可分解成两条路径 i，... , 2和2，... , j, 相加比较，取最短者为当前求得的从i到j的中间点序号不大于2的最短路径。

以此类推。。。

算法的基本思想是：

从最初的邻接矩阵A0开始，递推地生成矩阵序列A1，A2，。。。，An

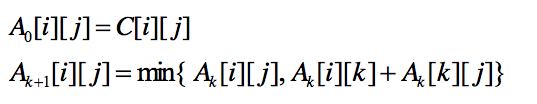
若要求的最短路径本身，还必须要设置一个路径矩阵P[n][n]，在第k次迭代中求得的path[i][j]，是从i到j的中间点序号不大于k的最短路径上顶点i的后继顶点。算法结束时，由path[i][j]的值就可以得到从i到j的最短路径上的各个顶点。

计算A矩阵序列方法：十字交叉法

http://blog.csdn.net/winbobob/article/details/38272679