java面试必知必会——排序

二、排序

时间复杂度分析

排序算法	平均时间复杂度	最好	最坏	空间复杂度	稳定性
冒泡	O(n²)	O(n)	O(n²)	O(1)	稳定
选择	O(n²)	O(n²)	O(n²)	O(1)	不稳定
插入	O(n²)	O(n)	O(n²)	O(1)	稳定
希尔	O(n^1.3)	O(n)	O(n²)	O(1)	不稳定
堆	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	不稳定
快排	O(nlogn)	O(nlogn)	O(n²)	O(logn)	不稳定
归并	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定
计数	O(n+k)	O(n+k)	O(n+k)	O(k)	稳定
基数	O(n x k)	O(n x k)	O(n x k)	O(n+k)	稳定
桶	O(n+k)	O(n+k)	O(n²)	O(n+k)	稳定

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。

不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。

时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。

空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。

冒泡排序

• 思路：

  • 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
  • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
  • 针对所有的元素重复以上的步骤，除了最后一个；
  • 重复步骤1~3，直到排序完成。

• 动图：

  

• 代码：

public static int[] bubbleSort(int[] array){
    if(array.length > 0){
        for (int i = 0; i < array.length; i++) {
            // array.length - 1 - i的解释：
            // -1表示最后一位不用重复交换步骤
            // -i表示每次排序都会有一个已经排好序了，-i就是表示末尾已经有i个元素排好序，不用再去遍历他们
            for (int j = 0; j < array.length - 1 - i; j++) {
                if(array[j] > array[j+1]){
                    int temp = array[j];
                    array[j] = array[j+1];
                    array[j+1] = temp;
                }
            }
        }
    }
    return array;
}

选择排序

• 思路：

  • 将数组分为有序区和无序区，刚刚开始时，有序区大小为0，无序区大小为整个数组；
  • 找出无序区中最小的元素，与无序区的第一个元素交换，就会变成有序区的一部分；
  • n-1趟后就全变成有序区了。

• 动图：

  

• 代码：

public static int[] selectionSort(int[] array){
    if(array.length > 0){
        // 先选定有序区的边界，刚刚开始时0
        for(int i = 0; i < array.length; i++){
            //选定无序区最小元素要出现的位置的索引
            int minIndex = i;
            //遍历无序区，将最小的位置放到索引处
            for (int j = i; j < array.length; j++) {
                if(array[j] < array[minIndex]){
                    int temp = array[j];
                    array[j] = array[minIndex];
                    array[minIndex] = temp;
                }
            }
        }
    }
    return array;
}

插入排序

• 思路：

  • 从第一个元素开始，假定整个元素已经被排序了，被排序的区域称为有序区，其他称为无序区；
  • 从下一个元素开始，在有序区从后向前遍历，找到等于或小于这个元素的元素，插入到它后面；
    • 在比较时，如果被比较的元素大于这个元素，就将被比较的元素后移一位，注意！是后移，不是交换。
  • 一直重复这个步骤直到都被排序

• 动图：

  

• 代码：

public static int[] insertSort(int[] array){
    if(array.length > 0){
        // 注意：边界条件是array.length - 1
        for (int i = 0; i < array.length - 1; i++) {
            // 要插入的元素
            int cur = array[i + 1];
            // 有序区的最后一个元素
            int index = i;
            // 遍历有序区，如果被比较元素大于要插入元素，就往后移一位
            while(index >= 0 && cur < array[index]){
                array[index + 1] = array[index];
                index--;
            }
            // 找到对的位置插入进去
            array[index + 1] = cur;
        }
    }
    return array;
}

希尔排序

• 思路：

  • 设定一个初始增量gap，称为间隔
  • 间隔会将数组分为几部分，然后对这些部分依次进行简单插入排序
  • 排序之后数组会有序得多，小的数在前，大的数在后
  • 第二遍在对数组分组排序，然后更有序
  • 最后简单调整一下序列即可

• 示意图和动图：

  

动图：

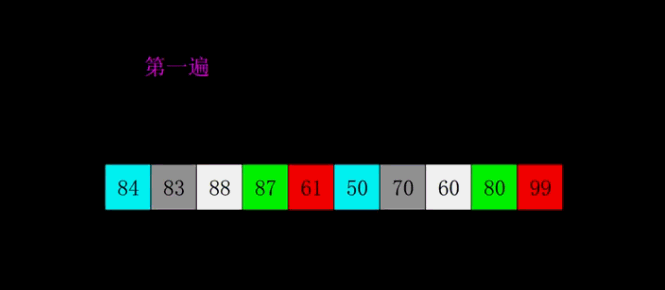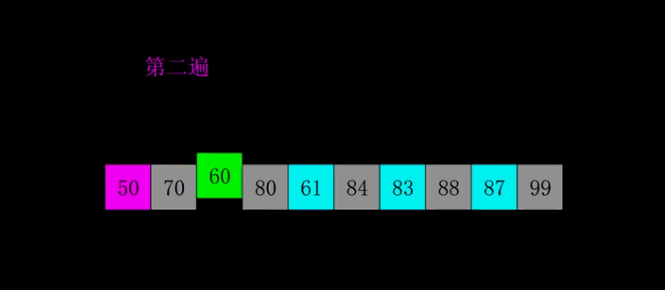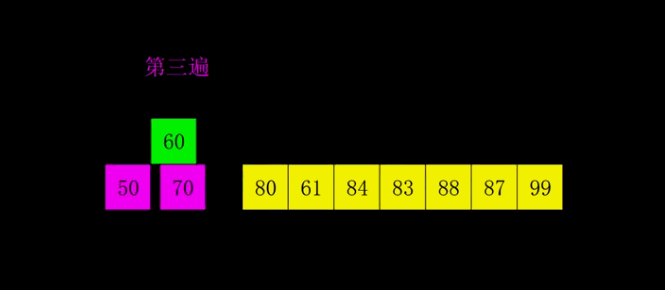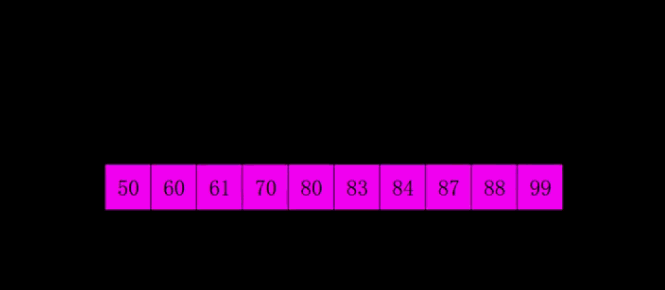
• 代码：

public static int[] shellSort(int[] array){
    if(array.length > 0){
        int len = array.length;
        // 初始间隔
        int gap = len / 2;
        while(gap > 0){
            for (int i = gap; i < len; i++) {
                int temp = array[i];
                // 这一步用来选同一组元素
                int index = i - gap;
                // 插入排序的思想
                while(index >= 0 && array[index] > temp){
                    array[index + gap] = array[index];
                    index -= gap;
                }
                array[index + gap] = temp;
            }
            // 间隔缩减
            gap /= 2;
        }
    }
    return array;
}

归并排序

• 思路：

  • 把长度为n的输入序列分成两个长度为n/2的子序列；
  • 对这两个子序列分别采用归并排序；（分治）
  • 将两个排序好的子序列合并成一个最终的排序序列。

• 动图：

  

  

• 代码：

public static int[] mergeSort(int[] array){
    if(array.length < 2){
        return array;
    }
    int mid = array.length / 2;
    int[] left = Arrays.copyOfRange(array, 0 , mid);
    int[] right = Arrays.copyOfRange(array, mid, array.length);
    return merge(mergeSort(left), mergeSort(right));
}

public static int[] merge(int[] left, int[] right){
    int[] result = new int[left.length + right.length];
    for (int i = 0, j = 0, index = 0; index < result.length; index++) {
        if(i >= left.length){               // 说明left数组已经遍历完了，添加上right数组就行
            result[index] = right[j++];
        }else if(j >= right.length){        // 说明right数组已经遍历完了，添加上left数组就行
            result[index] = left[i++];
        }else if(left[i] > right[j]){       // 如果左边的元素比右边元素大，右边元素存入result，指针后移
            result[index] = right[j++];
        }else{
            result[index] = left[i++];      // 如果右边的元素比左边元素大，左边元素存入result，指针后移
        }
    }
    return result;
}

快速排序

• 思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

• 思路：

  • 从数组中选择一个元素做为“基准”
  • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

• 动图：

  

• 代码

public static void quickSort(int[] arr, int left, int right) {
    if (left >= right) {
        return;
    }
    int x = arr[left];//以左边界的值为基准值
    int i = left;
    int j = right;
    while (i<j){
        // 当
        while(arr[i] < x)
            i++;
        while(arr[j] > x)
            j--;
        if (i<j){
            int temp=arr[i];
            arr[i]=arr[j];
            arr[j]=temp;
        }
    }
    //以j为分界值进行递归，基准值就不能是右边界的值
    quickSort(arr,left,j);
    quickSort(arr,j+1,right);
}

堆排序

• 思想：

  • 可以将堆看做是一个完全二叉树。并且，每个结点的值都大于等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于等于其左右孩子结点的值，称为小顶堆。
  • 将待排序列构造成一个大顶堆(或小顶堆)，整个序列的最大值(或最小值)就是堆顶的根结点，将根节点的值和堆数组的末尾元素交换，此时末尾元素就是最大值(或最小值)，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次大值(或次小值)，如此反复执行，最终得到一个有序序列。

• 思路：

  • 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；
  • 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
  • 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

• 动图：

  

• 代码

public static int[] heapSort(int[] array){
    int len = array.length;
    //初始化堆
    for(int i = len / 2 - 1; i >= 0; i--){
        heapAdjust(array, i, len);
    }
    //将堆顶的元素和最后一个元素交换，然后重新调整堆
    for(int i = len - 1; i > 0; i--){
        int temp = array[i];
        array[i] = array[0];
        array[0] = temp;
        heapAdjust(array, 0, i);
    }
    return array;
}

/**
     * 构造一个最大堆
     */
public static  void heapAdjust(int[] array, int index, int length){
    // 当前节点的下标
    int max = index;
    // 当前节点的左子节点下标
    int lchild = 2 * index;
    // 当前节点的右子节点下标
    int rchild = 2 * index + 1;
    // 左右子节点的值是否大于当前下标
    if(length > lchild && array[max] < array[lchild])
        max = lchild;
    if(length > rchild && array[max] < array[rchild])
        max = rchild;
    // 如果当前节点的值小于左右节点，就要将其和最大值交换位置，并且重新调整堆
    if(max != index){
        int temp = array[max];
        array[max] = array[index];
        array[index] = temp;
        heapAdjust(array, max, length);
    }
}

计数排序

• 思路：

  • 找出待排序的数组中最大和最小的元素；
  • 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
  • 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
  • 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

• 动图：

  

• 代码：

public static int[] countingSort(int[] array){
    if(array.length == 0){
        return array;
    }
    int bias ,min = array[0],max = array[0];
    //找出最小值和最大值
    for(int i = 0;i < array.length;i++){
        if(array[i] < min){
            min = array[i];
        }
        if(array[i] > max){
            max = array[i];
        }
    }
    //偏差
    bias = 0 - min;
    //新开辟一个数组
    int[] bucket = new int[max - min +1];
    //数据初始化为0
    Arrays.fill(bucket, 0);
    for(int i = 0;i < array.length;i++){
        bucket[array[i] + bias] += 1;
    }

    int index = 0;
    for(int i = 0;i < bucket.length;i++){
        int len = bucket[i];
        while(len > 0){
            array[index++] = i - bias;
            len --;
        }
    }

    return array;
}

桶排序

• 思路：

  • 人为设置一个BucketSize，作为每个桶所能放置多少个不同数值（例如当BucketSize==5时，该桶可以存放｛1,2,3,4,5｝这几种数字，但是容量不限，即可以存放100个3）；
  • 遍历输入数据，并且把数据一个一个放到对应的桶里去；
  • 对每个不是空的桶进行排序，可以使用其它排序方法，也可以递归使用桶排序；
  • 从不是空的桶里把排好序的数据拼接起来。

• 动图：

  

  

• 代码：

public static ArrayList<Integer> BucketSort(ArrayList<Integer> array, int bucketSize) {
    if (array == null || array.size() < 2)
        return array;
    int max = array.get(0), min = array.get(0);
    // 找到最大值最小值
    for (int i = 0; i < array.size(); i++) {
        if (array.get(i) > max)
            max = array.get(i);
        if (array.get(i) < min)
            min = array.get(i);
    }
    int bucketCount = (max - min) / bucketSize + 1;
    ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketCount);
    ArrayList<Integer> resultArr = new ArrayList<>();
    //构造桶
    for (int i = 0; i < bucketCount; i++) {
        bucketArr.add(new ArrayList<Integer>());
    }
    //往桶里塞元素
    for (int i = 0; i < array.size(); i++) {
        bucketArr.get((array.get(i) - min) / bucketSize).add(array.get(i));
    }
    for (int i = 0; i < bucketCount; i++) {
        if (bucketSize == 1) {
            for (int j = 0; j < bucketArr.get(i).size(); j++)
                resultArr.add(bucketArr.get(i).get(j));
        } else {
            if (bucketCount == 1)
                bucketSize--;
            ArrayList<Integer> temp = BucketSort(bucketArr.get(i), bucketSize);
            for (int j = 0; j < temp.size(); j++)
                resultArr.add(temp.get(j));
        }
    }
    return resultArr;
}

基数排序

• 思路：

  • 取得数组中的最大数，并取得位数；
  • arr为原始数组，从最低位开始取每个位组成radix数组；
  • 对radix进行计数排序（利用计数排序适用于小范围数的特点）；

• 动图：

  

• 代码：

public static int[] RadixSort(int[] array) {
    if (array == null || array.length < 2)
        return array;
    // 1.先算出最大数的位数；
    int max = array[0];
    for (int i = 1; i < array.length; i++) {
        max = Math.max(max, array[i]);
    }
    int maxDigit = 0;
    while (max != 0) {
        max /= 10;
        maxDigit++;
    }
    int mod = 10, div = 1;
    ArrayList<ArrayList<Integer>> bucketList = new ArrayList<ArrayList<Integer>>();
    for(int i = 0; i < 10;i++){
        bucketList.add(new ArrayList<Integer>());
    }
    for(int i = 0;i < maxDigit;i++,mod *= 10 ,div *= 10){
        for(int j = 0;j < array.length;j++){
            int num = (array[j] % mod) / div;
            bucketList.get(num).add(array[j]);
        }
        int index = 0;
        for(int j = 0;j < bucketList.size();j++){
            for(int k = 0;k < bucketList.get(j).size();k++){
                array[index++] = bucketList.get(j).get(k);
            }
            bucketList.get(j).clear();
        }
    }

    return array;
}