[刷题] 70 Climbing Stairs

要求

• 楼梯共有n个台阶，每次上一个台阶或两个台阶，一共有多少种上楼梯的方法？

示例

• 输入：n=3
• [1,1,1],[1,2,],[2,1]
• 输出：n=3

实现

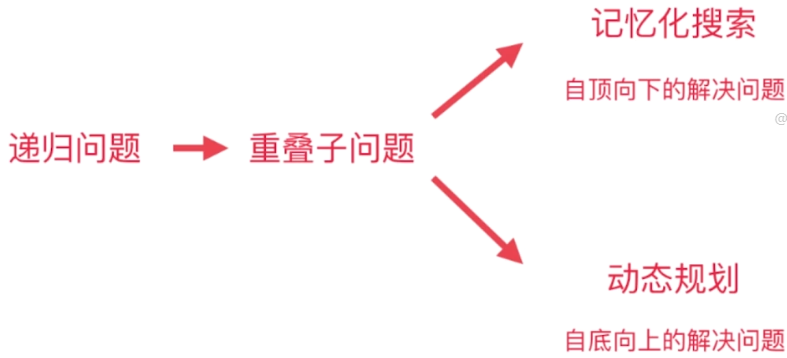
• 自顶向下（递归）

递归

 1 class Solution {
 2
 3 private:
 4     int calcWays(int n){
 5
 6         if( n == 0 || n == 1 )
 7             return 1;
 8
 9         return calcWays(n-1) + calcWays(n-2);
10     }
11
12 public:
13     int climbStairs(int n) {
14
15         return calcWays(n);
16     }
17 };

递归+记忆化搜索

 1 class Solution {
 2
 3 private:
 4     vector<int> memo;
 5
 6     int calcWays(int n){
 7
 8         if( n == 0 || n == 1 )
 9             return 1;
10
11         if( memo[n] == -1 )
12             memo[n] = calcWays(n-1) + calcWays(n-2);
13
14         return memo[n];
15     }
16
17 public:
18     int climbStairs(int n) {
19
20         memo = vector<int>(n+1,-1);
21         return calcWays(n);
22     }
23 };

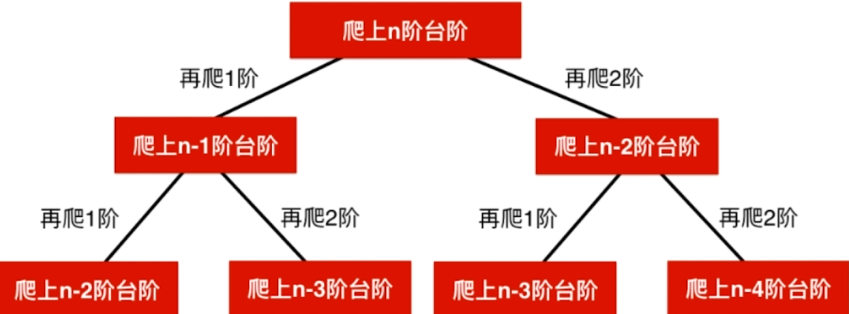
• 自底向上（动态规划）
  • 将原问题拆解成若干子问题，同时保存子问题的答案，使得每个问题只求解一次，最终获得原问题的答案

 1 class Solution {
 2
 3 public:
 4     int climbStairs(int n) {
 5
 6         vector<int> memo(n+1,-1);
 7
 8         memo[0] = 1;
 9         memo[1] = 1;
10         for( int i = 2 ; i <= n ; i ++ )
11             memo[i] = memo[i-1]+memo[i-2];
12         return memo[n];
13     }
14 };

相关

• 120 Triangle
• 64 Minimum Path Sum