AcWing09. 分组背包问题

有\(N\)组物品和一个容量是\(V\)的背包。

每组物品有若干个，同一组内的物品最多只能选一个。

每件物品的体积是\(v_{ij}\)，价值是\(w_{ij}\)，其中\(i\)是组号，\(j\)是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行有两个整数\(N\)，\(V\)，用空格隔开，分别表示物品组数和背包容量。

接下来有\(N\)组数据：

每组数据第一行有一个整数\(S_i\)，表示第\(i\)个物品组的物品数量；

每组数据接下来有\(S_i\)行，每行有两个整数\(v_{ij}\),\(w_{ij}\)，用空格隔开，分别表示第\(i\)个物品组的第\(j\)个物品的体积和价值；

输出格式

输出一个整数，表示最大价值。

数据范围

\(0<N,V≤100\)

\(0<S_i≤100\)

\(0<v_{ij},w_{ij}≤100\)

输入样例

3 5

2

1 2

2 4

1

3 4

1

4 5

输出样例：

8

---

思路：



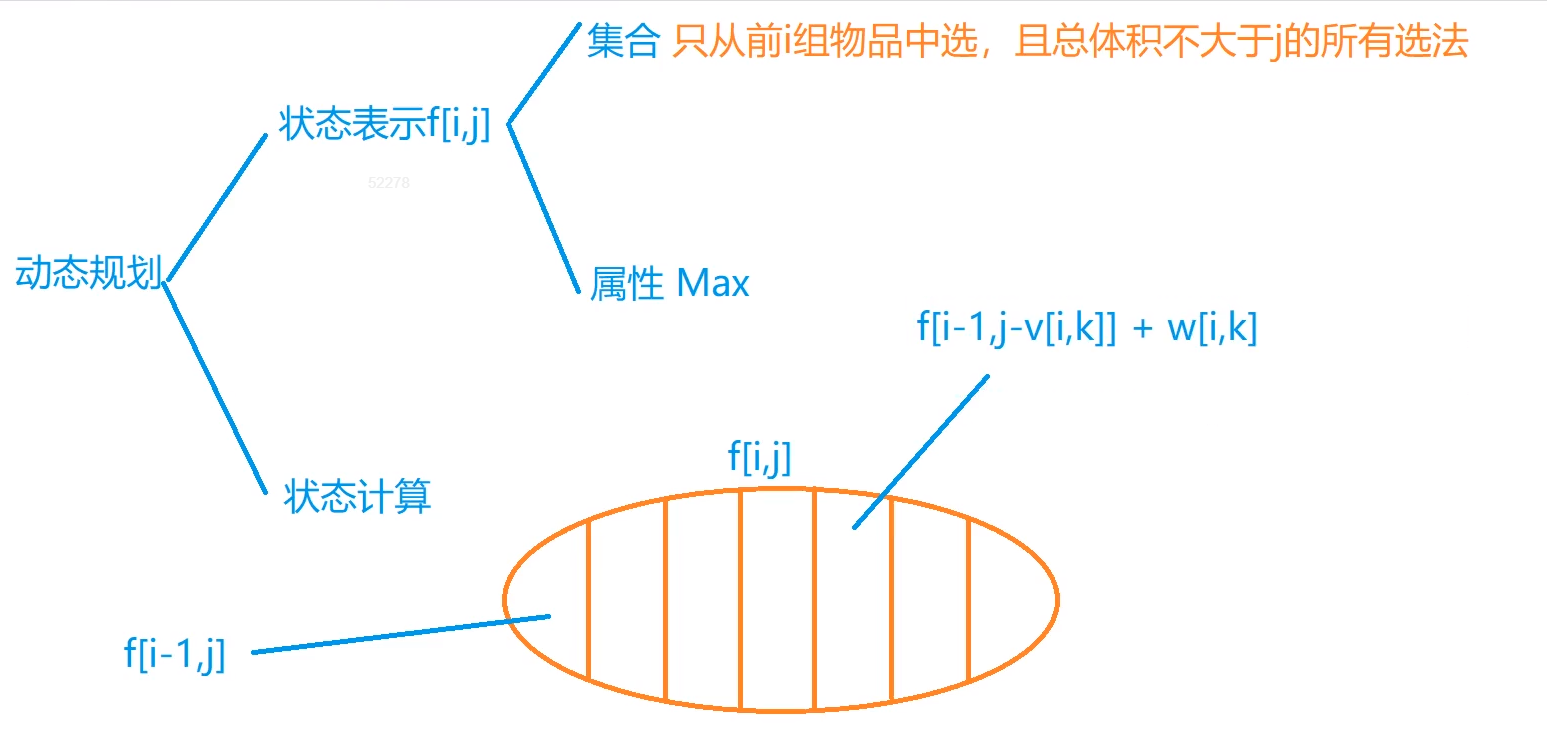
按照如上图所示的方式、对该集合进行集合划分、不难得出、不选\(i\)的状态表示为\(f[i - 1, j]\)、选\(i\)的状态表示为\(f[i - 1, j - v[i , k]] + w[i , k]\)，分析过程在我之前的01背包有过类似的

分析、此处不再赘述。指路链接

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int f[N][N], v[N][N], w[N][N];
int s[N];

int main()
{
    int n, m;
    cin >> n >> m;

    // input
    for(int i = 1 ; i <= n ; i ++ )
    {
        cin >> s[i];
        for(int j = 0 ; j < s[i] ; j ++ )
            cin >> v[i][j] >> w[i][j];
    }

    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = 0 ; j <= m ; j ++ )
        {
            // 不选的情况
            f[i][j] = f[i - 1][j];
            // 选的情况
            for(int k = 0 ; k < s[i] ; k ++ ){
                // 大于的时候才是这个状态
                if( j >= v[i][k])
                {
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
                }
            }
        }
    }

    // output
    cout << f[n][m] << endl;

    return 0;
}