Noip模拟41 2021.8.16

T1 你相信引力吗

对于区间的大小关系问题，往往使用单调栈来解决

这道题的优弧和劣弧很烦，考虑将其等价的转化

由于所有的合法情况绕过的弧都不会经过最高的冰锥，

又因为环可以任意亲定起点，这样可以直接把最大的点当作起点

那么我们所找的合法的答案就应该是：

在起点的右侧的冰锥配对，以及可以绕过来和起点配对的组合

这样就可以用单调栈维护，去重再开一个数组记录栈顶元素个数就行

 1 #include<bits/stdc++.h>
 2 #define LL long long
 3 using namespace std;
 4 inline int AE86(){
 5     int x=0,f=1; char ch=getchar();
 6     while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
 7     while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar();}
 8     return x*f;
 9 }
10 const int NN=1e7+5;
11 int n,a[NN],top,stk[NN],maxn,bin[NN];
12 LL ans;
13 namespace WSN{
14     inline short main(){
15         n=AE86();
16         for(register int i=1;i<=n;++i) a[i+n]=a[i]=AE86();
17         for(register int i=1;i<=n;++i) if(a[maxn]<a[i]) maxn=i;
18         for(register int i=maxn;i<=maxn+n-1;++i){
19             while(top&&stk[top]<a[i]) ++ans,--top;
20             stk[top]>a[i] ? (++ans):(ans+=bin[top]+(a[i]!=a[maxn]));
21             stk[++top]=a[i];
22             bin[top]=(a[i]==stk[top-1]?(bin[top-1]+1):(1));
23         }
24         while(top>2){
25             if(stk[top]==stk[2]) break;
26             ++ans,--top;
27         }
28         printf("%lld\n",ans);
29         return 0;
30     }
31 }
32 signed main(){return WSN::main();}

T2 marshland

一眼网络流，可是忘记了$dinic$，考场上比较傻眼

不过没事，这不是最大流，费用流我还没学过，所以就没什么抱怨的

这种题比较套路的做法是一个偶点旁边有上下左右四个奇点，在奇数行的和偶点的入点连边

偶数行的和偶点的出点连边，最后大概长这样：

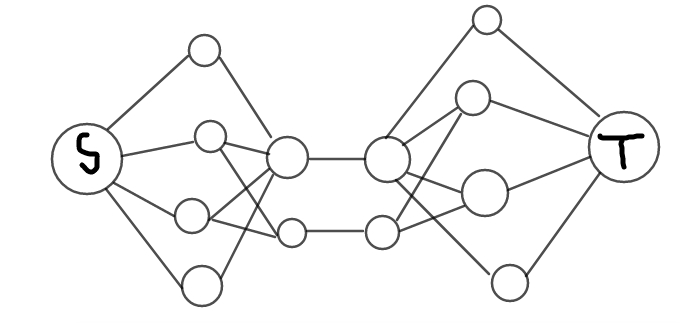
然后跑费用流$EK$板子，稍微魔改一下，跑的过程中记录答案就行

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 inline int AE86(){
 4     int x=0,f=1; char ch=getchar();
 5     while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
 6     while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar();}
 7     return x*f;
 8 }
 9 const int NN=1100,inf=2e9,MM=1e6+5;
10 int n,m,k,S,T,g[NN][NN];
11 int maxflow,mincost,ans,sum;
12 int pre[MM],incf[MM],dis[MM];
13 bool vis[MM],jin[NN][NN];
14 struct SNOW{int to,next,flow,val;}; SNOW e[MM<<1]; int head[MM],rp=1;
15 inline void add(int x,int y,int w,int c){
16     e[++rp]=(SNOW){y,head[x],w,c}; head[x]=rp;
17     e[++rp]=(SNOW){x,head[y],0,-c};head[y]=rp;
18 }
19 queue<int> q;
20 inline bool spfa(){
21     memset(dis,-0x3f,sizeof(dis));
22     memset(vis,0,sizeof(vis));
23     dis[S]=0; vis[S]=1; q.push(S); incf[S]=1<<30;
24     while(!q.empty()){
25         int x=q.front(); q.pop(); vis[x]=0;
26         for(register int i=head[x],y;i;i=e[i].next){
27             if(!e[i].flow) continue;
28             if(dis[y=e[i].to]<dis[x]+e[i].val){
29                 dis[y]=dis[x]+e[i].val;    pre[y]=i;
30                 incf[y]=min(incf[x],e[i].flow);
31                 if(!vis[y]) vis[y]=1,q.push(y);
32             }
33         }
34     }
35     if(dis[T]<0) return 0;
36     return 1;
37 }
38 inline void EK(){
39     while(spfa()){
40         int x=T;
41         if(maxflow+incf[T]>m) break;
42         maxflow+=incf[T];
43         mincost=max(mincost,mincost+dis[T]*incf[T]);
44         while(x!=S){
45             int i=pre[x];
46             e[i].flow-=incf[T];
47             e[i^1].flow+=incf[T];
48             x=e[i^1].to;
49         }
50         ans=min(ans,sum-mincost);
51     }
52 }
53 inline int id(int x,int y,int opt){return n*(x-1)+y+opt*n*n;}
54 namespace WSN{
55     inline short main(){
56         n=AE86(); m=AE86(); k=AE86(); S=n*n*2+1; T=S+1;
57         for(register int i=1;i<=n;++i) for(register int j=1;j<=n;++j){
58             g[i][j]=AE86(); sum+=g[i][j];
59             if(!g[i][j])
60                 if(i&1) add(S,id(i,j,0),1,0);
61                 else add(id(i,j,0),T,1,0);
62         }
63         for(register int i=1;i<=k;++i) jin[AE86()][AE86()]=1;
64         for(register int i=1;i<=n;++i) for(register int j=1;j<=n;++j) if(g[i][j]){
65             if(i&1){
66                 if(j-1>0&&!jin[i][j-1]) add(id(i,j-1,0),id(i,j,0),1,0);
67                 if(j+1<=n&&!jin[i][j+1]) add(id(i,j+1,0),id(i,j,0),1,0);
68                 if(i+1<=n&&!jin[i+1][j]) add(id(i,j,1),id(i+1,j,0),1,0);
69                 if(i-1>0&&!jin[i-1][j]) add(id(i,j,1),id(i-1,j,0),1,0);
70             }else{
71                 if(i+1<=n&&!jin[i+1][j]) add(id(i+1,j,0),id(i,j,0),1,0);
72                 if(i-1>0&&!jin[i-1][j]) add(id(i-1,j,0),id(i,j,0),1,0);
73                 if(j-1>0&&!jin[i][j-1]) add(id(i,j,1),id(i,j-1,0),1,0);
74                 if(j+1<=n&&!jin[i][j+1]) add(id(i,j,1),id(i,j+1,0),1,0);
75             }add(id(i,j,0),id(i,j,1),1,g[i][j]);
76         }
77         ans=sum; EK();
78         printf("%d\n",ans);
79         return 0;
80     }
81 }
82 signed main(){return WSN::main();}

T3 party？

考场上做完了预处理的工作，然后就傻眼了，因为T2看出网络流

这题就没有往那里想，网络流可以拿到暴力分其实

先用$bitset$预处理出每一条路径有多少中可能选择的特产，线段树+树剖比较显然

然后就是考虑如何满足题意找到最大合法情况

我们建一个二分图，左部点是人，右部点是特产，每个人分裂成答案个

这样的话，让二分图实现完美匹配即可。

问题转化成要找到一个满足可以二分图完美匹配的最大的$k$

然后引入一个霍尔定理（雾）

一个二分图(G)存在完美匹配, 当且仅当(X)中的任意(k)个点都至少与(Y)中的(k)个点邻接.

左部$c*k$个点只有$c$种邻接关系不同的点，所以$2^c$枚举子集，用$bitset$取并找邻接点个数

则最大的$k$即为邻接点个数和子集个数比值最小值

 1 #include<bits/stdc++.h>
 2 #define bs bitset<1005>
 3 #define lid (id<<1)
 4 #define rid (id<<1|1)
 5 using namespace std;
 6 inline int AE86(){
 7     int x=0,f=1; char ch=getchar();
 8     while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
 9     while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar();}
10     return x*f;
11 }
12 inline int min(int a,int b){return a<b?a:b;}
13 inline void swap(int &a,int &b){a^=b^=a^=b;}
14 const int NN=3e5+1;
15 bs b[NN];
16 int n,m,q,a[NN],ci[NN],num,ans,c,lca;
17 int dfn[NN],rk[NN],son[NN],fa[NN],siz[NN],dep[NN],top[NN],cnt;
18 struct SNOW{int to,next;};SNOW e[NN<<1]; int head[NN],rp;
19 inline void add(int x,int y){
20     e[++rp]=(SNOW){y,head[x]};head[x]=rp;
21     e[++rp]=(SNOW){x,head[y]};head[y]=rp;
22 }
23 struct SNOWtree{
24     int ll[NN<<2],rr[NN<<2]; bs te[NN<<2];
25     inline void pushup(int id){
26         if(ll[id]==rr[id]) return;
27         te[id]=te[lid]|te[rid];
28     }
29     inline void build(int id,int l,int r){
30         ll[id]=l;rr[id]=r;
31         if(l==r){te[id][a[rk[l]]]=1;return;}
32         int mid=l+r>>1;
33         build(lid,l,mid); build(rid,mid+1,r);
34         pushup(id);
35     }
36     inline bs query(int id,int l,int r){
37         if(l<=ll[id]&&rr[id]<=r) return te[id];
38         int mid=ll[id]+rr[id]>>1; bs ans;
39         if(l<=mid) ans|=query(lid,l,r);
40         if(r>mid) ans|=query(rid,l,r);
41         return ans;
42     }
43 }tr;
44 inline void dfs1(int f,int x){
45     dep[x]=dep[f]+1; siz[x]=1;
46     for(register int i=head[x],y;i;i=e[i].next) if((y=e[i].to)!=f){
47         dfs1(x,y); siz[x]+=siz[y];
48         if(siz[son[x]]<siz[y]) son[x]=y;
49     }
50 }
51 inline void dfs2(int x,int t){
52     top[x]=t; dfn[x]=++cnt; rk[cnt]=x;
53     if(x!=t) b[x]=b[fa[x]]; b[x].set(a[x]);
54     if(son[x]) dfs2(son[x],t);
55     for(register int i=head[x],y;i;i=e[i].next) if((y=e[i].to)!=fa[x]&&y!=son[x]) dfs2(y,y);
56 }
57 inline int LCA(int x,int y){
58     while(top[x]!=top[y]){
59         if(dep[top[x]]<dep[top[y]]) swap(x,y);
60         x=fa[top[x]];
61     }if(dfn[x]>dfn[y]) swap(x,y);
62     return x;
63 }
64 inline bs query(int x,int y){
65     bs ans;
66     while(top[x]!=top[y]){
67         if(dep[top[x]]<dep[top[y]]) swap(x,y);
68         ans|=b[x];
69         x=fa[top[x]];
70     }if(dfn[x]>dfn[y]) swap(x,y);
71     ans|=tr.query(1,dfn[x],dfn[y]);
72     return ans;
73 }
74 namespace WSN{
75     inline short main(){
76         n=AE86();m=AE86();q=AE86(); if(!q) return 0;
77         for(register int i=2;i<=n;++i) fa[i]=AE86(),add(i,fa[i]);
78         for(register int i=1;i<=n;++i) a[i]=AE86();
79         dfs1(0,1);dfs2(1,1);tr.build(1,1,n);
80         while(q--){
81             c=AE86(); bs tmp[6]; ci[1]=AE86(); ci[2]=AE86();
82             ans=0x3fffffff; lca=LCA(ci[1],ci[2]);
83             for(register int i=3;i<=c;++i) ci[i]=AE86(),lca=LCA(lca,ci[i]);
84             for(register int i=1;i<=c;++i) tmp[i]=query(ci[i],lca);
85             for(register int s=1;s<(1<<c);++s){
86                 bs cc;num=0;
87                 for(register int i=0;i<c;++i) if((1<<i)&s) ++num,cc|=tmp[i+1];
88                 ans=min(ans,(int)cc.count()/num);
89             }printf("%d\n",ans*c);
90         }
91         return 0;
92     }
93 }
94 signed main(){return WSN::main();}

T4 半夜

沽沽沽