BUAA_2020_软件工程_个人项目作业

作业抬头(1')

项目	内容
这个作业属于哪个课程	2020春季计算机学院软件工程(罗杰任健)
这个作业的要求在哪里	个人项目作业
我在这个课程的目标是	了解软件工程的技术，掌握工程化开发的能力
这个作业在哪个具体方面帮助我实现目标	初步学习掌握测试和效能分析等工具
教学班级	006
项目地址	https://github.com/Reliacrt/IntersectionSolution.git

解题思路描述。即刚开始拿到题目后，如何思考，如何找资料的过程。（3'）

本次作业需要求交点的个数，所以我采取的办法是计算出所有的交点并插入一个集合中，最后输出集合内元素的个数。

所以查找了直线直线交点、直线圆交点、圆圆交点的计算方法，具体的计算方法由代码说明一节给出。

设计实现过程。设计包括代码如何组织，比如会有几个类，几个函数，他们之间关系如何，关键函数是否需要画出流程图？单元测试是怎么设计的？（4'）

类说明

Point类：用来保存计算得到的交点结果，并重载了比较相关操作符，便于使用set容器
Shape类：Line和Circle的基类，用来提供统一的抽象接口intersect
Line : Shape类：Shape的子类，用来描述直线
Circle : Shape类：Shape的子类，用来描述圆

函数说明(关键)(intersect接口背后使用的函数)

以下三个函数返回值都是vector<Point>：

line_inter_line(Shape*, Shape*)：直线与直线交点函数
line_inter_circle(Shape*, Shape*)：直线与圆交点函数
circle_inter_circle(Shape*, Shape*)：圆与圆交点函数

类、函数关系说明

为避免重复代码，子类对intersect接口的实现统统调用的上述三个函数，在Shape类中保留类型字段用以区分Line还是Circle，然后分派到不同的函数。

关键函数流程由数学计算的方法给出。

单元测试设计

由于子类的成员函数的实现都是通过的上述三个关键函数，所以单元测试就针对上述三个函数写了三个单元测试：

线线：分别测试相交一点和不相交的情况（4个测试用例）
线圆：分别测试相交两点、相切和不相交的情况（4个测试用例）
圆圆：分别测试相交两点、相切和不相交的情况（3个测试用例）

记录在改进程序性能上所花费的时间，描述你改进的思路，并展示一张性能分析图（由 VS 2019 的性能分析工具自动生成），并展示你程序中消耗最大的函数。（3'）

性能分析图

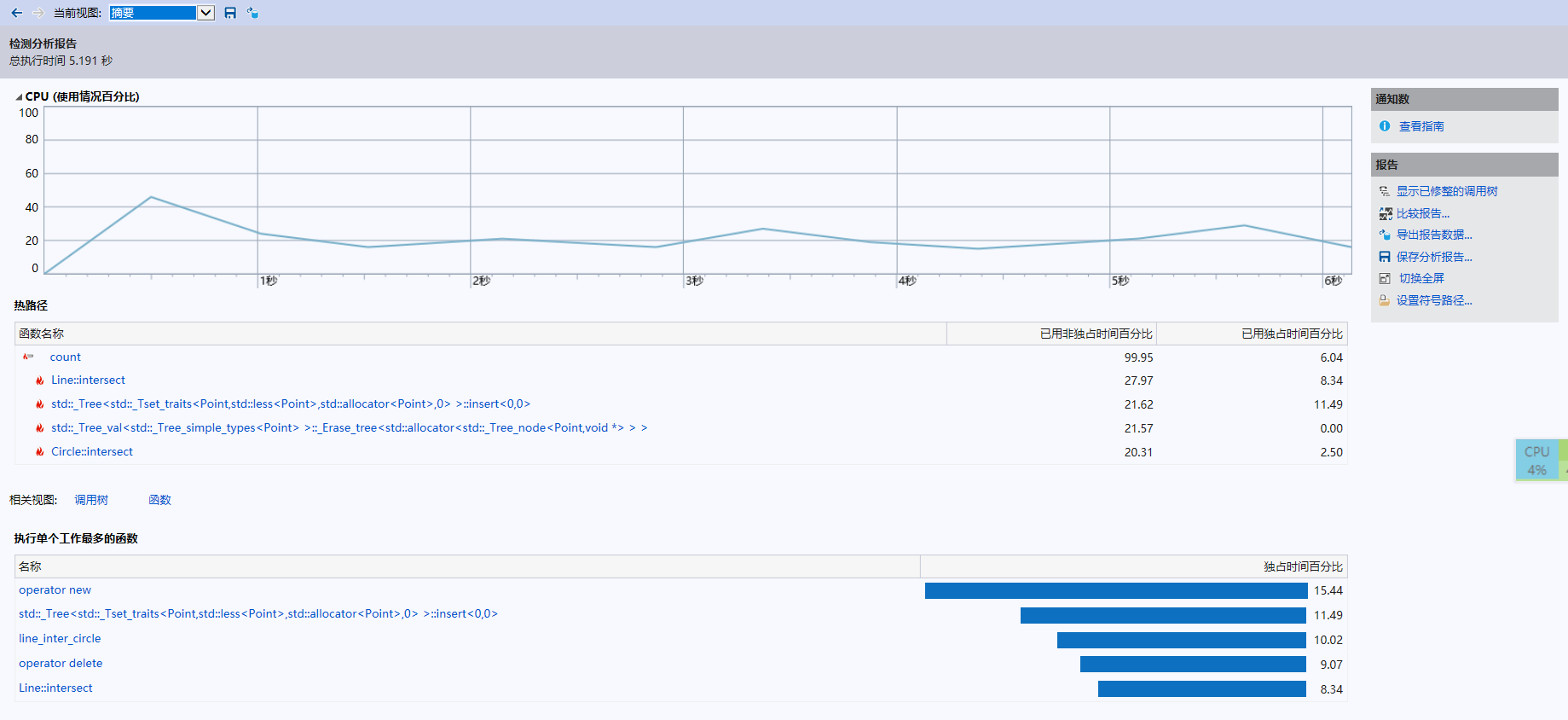
函数运行时间

函数名	调用数	已用非独占时间百分比	已用独占时间百分比	平均已用非独占时间
performance	1	100	0.02	5,190.55
__scrt_common_main_seh	1	100	0	5,190.67
main	1	100	0	5,190.57
mainCRTStartup	1	100	0	5,190.67
count	1	99.95	6.04	5,188.20
line_inter_circle	338,605	35.5	10.02	0.01
Line::intersect	239,418	27.97	8.34	0.01
std::_Tree::insert	533,463	21.62	11.49	0
std::_Tree_val::_Erase_tree	533,463	21.57	7.25	55.98
Circle::intersect	260,082	20.31	2.5	0
operator delete	1,066,945	18.33	3.43	0
std::vector::_Emplace_reallocate	533,463	16.81	3.09	0
operator new	1,156,991	15.44	15.44	0
operator delete	1,066,945	14.9	9.07	0
__security_check_cookie	598,690	7.34	7.34	0
std::_Tree_val::_Insert_node	533,463	7.31	7.31	0
_free	1,066,945	5.83	5.83	0
sqrt<int,void>	338,605	2.81	2.81	0
rand	6,000	0.01	0.01	0

这是采用Instrumentation的方式测试后的函数部分的时间数据，由于是自动选择的标记函数，3个关键函数只标记了line_inter_circle，但是即便只标记了他，也可以从上述数据看出其消耗时间，在计算交点的过程中是最大的，而且后续的插入set消耗的时间更是占了这个程序的20%以上，更小一级的操作符也就是内存分配函数new和delete，也是消耗时间超过了20%，所以这就是3个优化程序运行时间的方向：

优化交点的计算：可以通过简化计算过程优化交点计算耗时
优化最后统计交点所用的容器：set容器内部使用的红黑树，插入消耗相当大
优化中间计算过程所用的容器：中间计算所用的vector不断创建并删除，这是大量的内存分配工作

我觉得我能做的优化只有第三点了，目前只做了基本的将函数内联的操作。

代码说明。展示出项目关键代码，并解释思路与注释说明。（3'）

line_inter_line

inline vector<Point> line_inter_line(Shape* s1, Shape* s2)

{

	double x, y;

	Line* l1 = (Line*)s1;

	Line* l2 = (Line*)s2;

	vector<Point> ret;

	auto a1 = l1->x_coeff, a2 = l2->x_coeff;

	auto b1 = l1->y_coeff, b2 = l2->y_coeff;

	auto c1 = l1->c_coeff, c2 = l2->c_coeff;

	if (a1 * b2 - a2 * b1 != 0)

	{

		x = ((double)c2 * b1 - (double)c1 * b2) / ((double)a1 * b2 - (double)a2 * b1);

		y = ((double)c1 * a2 - (double)c2 * a1) / ((double)a1 * b2 - (double)a2 * b1);

		ret.push_back(Point(x, y));

	}

	return ret;

}

线线交点计算思路

首先直线在内部转化为$Ax+By+C=0$的表示；然后根据线性代数：

\[\begin{bmatrix} A_1 & B_1 \\ A_2 & B_2 \\ \end{bmatrix}
\begin{bmatrix} x \\ y \\ \end{bmatrix} =
\begin{bmatrix} C_1 \\ C_2 \\ \end{bmatrix}
\]

可得：

\[\begin{bmatrix} x \\ y \\ \end{bmatrix}=\begin{bmatrix} A_1 & B_1 \\ A_2 & B_2 \\ \end{bmatrix} ^{-1}\begin{bmatrix} C_1 \\ C_2 \\ \end{bmatrix}={1\over A_1B_2-A_2B_1}\begin{bmatrix} {B_2} & {-B_1} \\ {-A_2} & {A_1} \\ \end{bmatrix} \begin{bmatrix} C_1 \\ C_2 \\ \end{bmatrix}
\]

进一步可得：

\[x = {B_2C_1-B_1C_2 \over A_1B_2-A_2B_1} \\y = {A_1C_2-A_2C_1 \over A_1B_2-A_2B_1}
\]

line_inter_circle

inline vector<Point> line_inter_circle(Shape* s1, Shape* s2)

{

	Line* l = (Line*)s1;

	Circle* c = (Circle*)s2;

	vector<Point> ret;

	auto A = l->x_coeff, B = l->y_coeff, C = l->c_coeff;

	auto x0 = c->x_coeff, y0 = c->y_coeff, r = c->r_coeff;

	const int ssum_a_b = SSUM(A, B);

	const double squa_ssum = sqrt(ssum_a_b);

	double d = abs(A * x0 + B * y0 + C) / squa_ssum;

	if (d > r) return ret;

	double x_d = ((double)-A * C + (double)B * B * x0 - (double)A * B * y0) / ssum_a_b;

	double y_d = ((double)-B * C - (double)A * B * x0 + (double)A * A * y0) / ssum_a_b;

	if (r > d) // 相交于两点

	{

		double ano_d = sqrt((double)r * r - d * d);

		double vec_x = 1.0 * (-B) / squa_ssum;

		double vec_y = 1.0 * (A) / squa_ssum;

		ret.push_back(Point(x_d + vec_x * ano_d, y_d + vec_y * ano_d));

		ret.push_back(Point(x_d - vec_x * ano_d, y_d - vec_y * ano_d));

	}

	if (r == d) // 相切于一点

	{

		ret.push_back(Point(x_d, y_d));

	}

	return ret;

}

线圆交点计算思路

首先确定圆心与直线的距离，采用点到直线距离公式：

\[d = {|Ax_0+By_0+C|\over \sqrt{A^2+B^2}}
\]

然后比较$d$与$r$的大小判断有几个交点：

$d<r$：2个
$d=r$：1个
$d>r$：0个

然后求过圆心与该直线的垂线与该直线的交点（如果上一步判断只有一个交点，则该点即交点，停止计算）：

\[({-AC+B^2x_0-ABy_0 \over A^2+B^2},
{-BC-ABx_0+A^2y_0 \over A^2+B^2})
\]

然后根据以上交点和直线方程以及$\sqrt{r^2-d^2}$求出两交点：

\[({-AC+B^2x_0-ABy_0 \over A^2+B^2} \pm {-B\over \sqrt{A^2+B^2}} \times \sqrt{r^2-d^2},
{-BC-ABx_0+A^2y_0 \over A^2+B^2} \pm {A \over \sqrt{A^2+B^2}} \times \sqrt{r^2-d^2})
\]

circle_inter_circle

inline vector<Point> circle_inter_circle(Shape* s1, Shape* s2)

{

	Circle* c1 = (Circle*)s1;

	Circle* c2 = (Circle*)s2;

	vector<Point> ret;

	auto x1 = c1->x_coeff, y1 = c1->y_coeff, r1 = c1->r_coeff;

	auto x2 = c2->x_coeff, y2 = c2->y_coeff, r2 = c2->r_coeff;

	auto d_2 = SSUM(x2 - x1, y2 - y1);

	auto r_r_2 = SQUA(r1 + r2);

	if (r_r_2 >= d_2)

	{

		Shape* line = new Line(

			2 * (x2 - x1),

			2 * (y2 - y1),

			x1 * x1 - x2 * x2 + y1 * y1 - y2 * y2 - r1 * r1 + r2 * r2);

		return line_inter_circle(line, s1);

	}

	return ret;

}

圆圆交点计算思路

首先确定两圆心的距离：$d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

然后比较$d$与$r$的大小判断有几个交点：

$d<r_1+r_2$：2个
$d=r_1+r_2$：1个
$d>r_1+r_2$：0个

然后将两方程相减得到交点的直线方程，转换圆圆交点为线圆交点：

\[(x-x_1)^2+(y-y_1)^2 = r_1^2 \\
(x-x_2)^2+(y-y_2)^2 = r_1^2 \\
\]

相减得：

\[2(x_2-x_1)x+2(y_2-y_1)y+x_1^2-x_2^2+y_1^2-y_2^2+r_2^2-r_1^2=0
\]

将该方程与任意一个圆方程联立采用线圆交点计算即可得结果。

Code Analysis的警告消除

通过输出部分可以看出，两个成功（项目和测试项目），没有错误和警告。

时间花费(1')

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	10	10
· Estimate	· 估计这个任务需要多少时间	10	10
Development	开发	325	410
· Analysis	· 需求分析 (包括学习新技术)	20	30
· Design Spec	· 生成设计文档	30	30
· Design Review	· 设计复审 (和同事审核设计文档)	\	\
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	15	0
· Design	· 具体设计	30	50
· Coding	· 具体编码	120	180
· Code Review	· 代码复审	30	30
· Test	· 测试（自我测试，修改代码，提交修改）	80	90
Reporting	报告	60	60
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	20	20
	合计	395	480

本次项目的收获

主要是学会了VS项目中单元测试的使用和性能探查器的使用（我的电脑CPU Sampling不可用），以及利用Code Analysis消除错误和警告来完善代码。