如何直观的解释back propagation算法？

转自:知乎-https://www.zhihu.com/question/27239198

作者：匿名用户
链接：https://www.zhihu.com/question/27239198/answer/89853077
来源：知乎
著作权归作者所有，转载请联系作者获得授权。

BackPropagation算法是多层神经网络的训练中举足轻重的算法。
简单的理解，它的确就是复合函数的链式法则，但其在实际运算中的意义比链式法则要大的多。
要回答题主这个问题“如何直观的解释back propagation算法？” 需要先直观理解多层神经网络的训练。

机器学习可以看做是数理统计的一个应用，在数理统计中一个常见的任务就是拟合，也就是给定一些样本点，用合适的曲线揭示这些样本点随着自变量的变化关系。

深度学习同样也是为了这个目的，只不过此时，样本点不再限定为(x, y)点对，而可以是由向量、矩阵等等组成的广义点对(X,Y)。而此时，(X,Y)之间的关系也变得十分复杂，不太可能用一个简单函数表示。然而，人们发现可以用多层神经网络来表示这样的关系，而多层神经网络的本质就是一个多层复合的函数。借用网上找到的一幅图[1]，来直观描绘一下这种复合关系。
<img src="https://pic4.zhimg.com/808254232cd4983cac374c5cc2a1fc87_b.png" data-rawwidth="400" data-rawheight="282" class="content_image" width="400">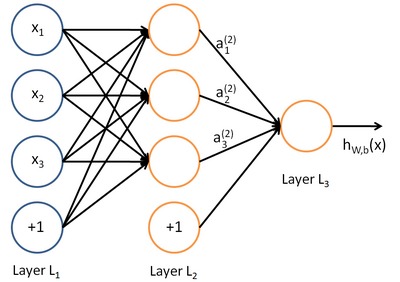

其对应的表达式如下：

<img src="https://pic4.zhimg.com/e62889afe359c859e9a6a1ad2a432ebb_b.png" data-rawwidth="474" data-rawheight="128" class="origin_image zh-lightbox-thumb" width="474" data-original="https://pic4.zhimg.com/e62889afe359c859e9a6a1ad2a432ebb_r.png">上面式中的Wij就是相邻两层神经元之间的权值，它们就是深度学习需要学习的参数，也就相当于直线拟合y=k*x+b中的待求参数k和b。

上面式中的Wij就是相邻两层神经元之间的权值，它们就是深度学习需要学习的参数，也就相当于直线拟合y=k*x+b中的待求参数k和b。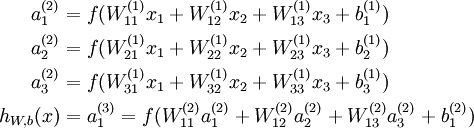

和直线拟合一样，深度学习的训练也有一个目标函数，这个目标函数定义了什么样的参数才算一组“好参数”，不过在机器学习中，一般是采用成本函数（cost function），然后，训练目标就是通过调整每一个权值Wij来使得cost达到最小。cost函数也可以看成是由所有待求权值Wij为自变量的复合函数，而且基本上是非凸的，即含有许多局部最小值。但实际中发现，采用我们常用的梯度下降法就可以有效的求解最小化cost函数的问题。

梯度下降法需要给定一个初始点，并求出该点的梯度向量，然后以负梯度方向为搜索方向，以一定的步长进行搜索，从而确定下一个迭代点，再计算该新的梯度方向，如此重复直到cost收敛。那么如何计算梯度呢？

假设我们把cost函数表示为, 那么它的梯度向量[2]就等于, 其中表示正交单位向量。为此，我们需求出cost函数H对每一个权值Wij的偏导数。而BP算法正是用来求解这种多层复合函数的所有变量的偏导数的利器。

我们以求e=(a+b)*(b+1)的偏导[3]为例。
它的复合关系画出图可以表示如下：
<img src="https://pic1.zhimg.com/ee59254c9432b47cfcc3b11eab3e5984_b.png" data-rawwidth="1383" data-rawheight="800" class="origin_image zh-lightbox-thumb" width="1383" data-original="https://pic1.zhimg.com/ee59254c9432b47cfcc3b11eab3e5984_r.png">在图中，引入了中间变量c,d。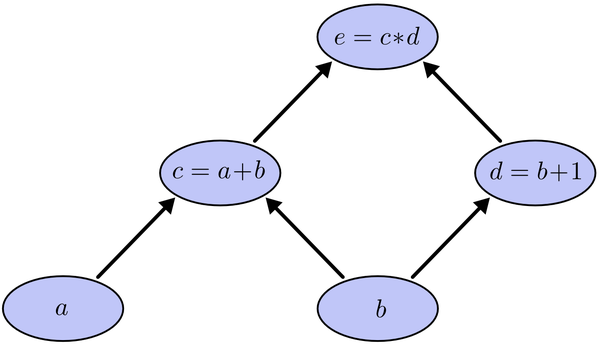在图中，引入了中间变量c,d。

为了求出a=2, b=1时，e的梯度，我们可以先利用偏导数的定义求出不同层之间相邻节点的偏导关系，如下图所示。
<img src="https://pic2.zhimg.com/986aacfebb87f4e9573fa2fe87f439d1_b.png" data-rawwidth="1405" data-rawheight="793" class="origin_image zh-lightbox-thumb" width="1405" data-original="https://pic2.zhimg.com/986aacfebb87f4e9573fa2fe87f439d1_r.png">利用链式法则我们知道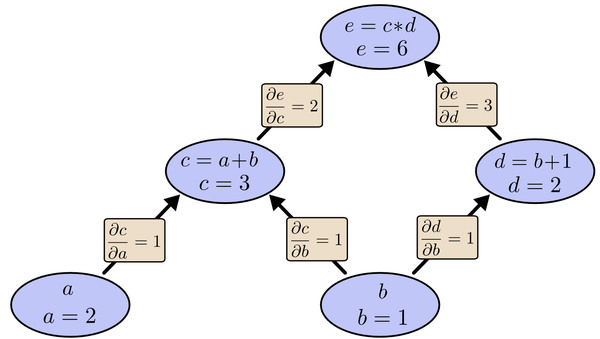：利用链式法则我们知道：
以及。

链式法则在上图中的意义是什么呢？其实不难发现，的值等于从a到e的路径上的偏导值的乘积，而的值等于从b到e的路径1(b-c-e)上的偏导值的乘积加上路径2(b-d-e)上的偏导值的乘积。也就是说，对于上层节点p和下层节点q，要求得，需要找到从q节点到p节点的所有路径，并且对每条路径，求得该路径上的所有偏导数之乘积，然后将所有路径的 “乘积” 累加起来才能得到的值。

大家也许已经注意到，这样做是十分冗余的，因为很多路径被重复访问了。比如上图中，a-c-e和b-c-e就都走了路径c-e。对于权值动则数万的深度模型中的神经网络，这样的冗余所导致的计算量是相当大的。

同样是利用链式法则，BP算法则机智地避开了这种冗余，它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。
正如反向传播(BP)算法的名字说的那样，BP算法是反向(自上往下)来寻找路径的。

从最上层的节点e开始，初始值为1，以层为单位进行处理。对于e的下一层的所有子节点，将1乘以e到某个节点路径上的偏导值，并将结果“堆放”在该子节点中。等e所在的层按照这样传播完毕后，第二层的每一个节点都“堆放"些值，然后我们针对每个节点，把它里面所有“堆放”的值求和，就得到了顶点e对该节点的偏导。然后将这些第二层的节点各自作为起始顶点，初始值设为顶点e对它们的偏导值，以"层"为单位重复上述传播过程，即可求出顶点e对每一层节点的偏导数。

以上图为例，节点c接受e发送的1*2并堆放起来，节点d接受e发送的1*3并堆放起来，至此第二层完毕，求出各节点总堆放量并继续向下一层发送。节点c向a发送2*1并对堆放起来，节点c向b发送2*1并堆放起来，节点d向b发送3*1并堆放起来，至此第三层完毕，节点a堆放起来的量为2，节点b堆放起来的量为2*1+3*1=5, 即顶点e对b的偏导数为5.

举个不太恰当的例子，如果把上图中的箭头表示欠钱的关系，即c→e表示e欠c的钱。以a, b为例，直接计算e对它们俩的偏导相当于a, b各自去讨薪。a向c讨薪，c说e欠我钱，你向他要。于是a又跨过c去找e。b先向c讨薪，同样又转向e，b又向d讨薪，再次转向e。可以看到，追款之路，充满艰辛，而且还有重复，即a, b 都从c转向e。

而BP算法就是主动还款。e把所欠之钱还给c，d。c，d收到钱，乐呵地把钱转发给了a，b，皆大欢喜。
------------------------------------------------------------------
【参考文献】
[1] 技术向：一文读懂卷积神经网络CNN
[2] Gradient
[3] http://colah.github.io/posts/2015-08-Backprop/
其他推荐网页：
1. tensorflow.org 的页面
2. Neural networks and deep learning