Mr. Kitayuta vs. Bamboos

Mr. Kitayuta vs. Bamboos

题目链接：http://codeforces.com/problemset/problem/505/E

参考：http://blog.csdn.net/qpswwww/article/details/46316647

贪心，二分

从数据规模上看，算法复杂度只能为O(n)或者O(nlgn)，似乎不能直接求值，考虑二分MAX将求值问题转化为判定性问题。然而考虑到砍伐后竹子高度变为0的特殊情况，考虑倒着做，即初始时每个竹子高度均为MAXi，每天晚上每个竹子会减少高度a[i]，每天白天可以选择对其中不超过K个竹子选择将其的高度增加P，并且保证任何时刻任何竹子高度均大于等于0，m天后是否可以让每个竹子高度均大于等于h[i]。

证明倒着推的正确性：只有在m天后每个竹子高度均大于等于h[i]，才能让所有的竹子按照原来正向的顺序，以和倒着做相同的操作反过来让每个竹子最终的高度小于等于MAXi，见下图，绿色线代表倒着推的话一根竹子的每天生长情况，蓝色线代表正着推的话一根竹子的每天生长情况(来自Codeforces官方题解)

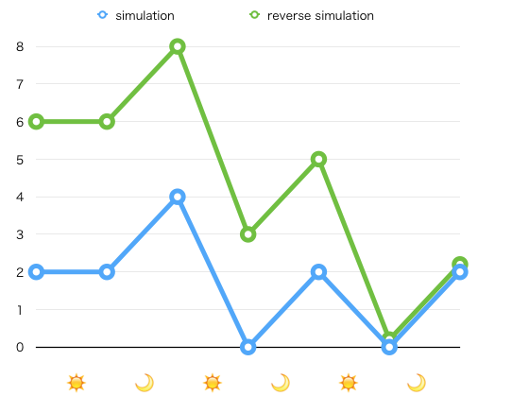
可以发现如果每天对这个竹子的操作相同的话，要想让最后的这个竹子的高度和倒着推的高度一样，之前每天正着推的高度都必须小于等于倒着推的高度。

首先计算从MAXi开始，最多经历多少天自由生长（减少高度a[i]），竹子的高度变为负数，然后用一个小顶堆维护竹子变为负数的天数（时间越小，越快变为负数），每天取k个竹子进行砍伐（拔高处理）。若存在某一天来不及拔高竹子(存在某个竹子的高度在这一天之前就变为0了)，就可以立刻判定m天后不能可以让每个竹子高度均大于等于h[i]。

现在我们让所有竹子倒过来生长，最终每个竹子高度均大于等于0后，就需要让每个竹子的高度拔高，使得它们最终高度大于等于h[i]，显然此时由于在生长过程中，每个竹子在任意时刻高度均大于等于0，故此时补充的操作无论是在何时发生都是一样的。这时直接通过数学方法，计算每个竹子和h[i]之间相差的高度以考虑需要补上多少次操作就够了。

这道题是看着题解跪着做完的Orz，感觉对二分的理解更深了一些，二分处理的都是判定性问题，不能直接求值。

代码如下：

 #include<cstdio>
 #include<queue>
 #include<iostream>
 #define N 100000
 #define LL long long
 #define mid ((l+r)>>1)
 using namespace std;
 const LL MAX=1e15;
 LL n,m,k,p,l,r;
 LL h[N+],a[N+];
 LL now[N+];
 typedef pair<LL,LL> P;
 struct cmp{
     bool operator()(P a,P b){
         return a.first>b.first;//小顶堆
     }
 };
 bool judge(LL x){
     priority_queue<P,vector<P>,cmp> q;
     for(LL i=;i<n;++i){
         now[i]=x;//刚开始竹子的高度为MAXi
         if(x-m*a[i]>=)continue;//不需要补充高度
         q.push(make_pair(x/a[i],i));//P(到零的天数,下标)
     }
     LL times=;//砍伐次数
     for(;times<=k*m;times++){
         if(q.empty())break;
         P temp=q.top();
         q.pop();
         if(temp.first<=times/k)return ;//来不及补充高度，竹子在k天前就长成负数
         LL index=temp.second;
         now[index]+=p;
         if(now[index]-m*a[index]>=)continue;//不需要补充高度
         q.push(make_pair(now[index]/a[index],index));
     }
     if(times>k*m)return ;
     for(int i=;i<n;++i){
         LL temp=m*a[i]+h[i]-now[i];
         if(temp<=)continue;
         else times+=((temp/p)+(LL)(temp%p!=));//到h[i]还需要多少次补充高度
         if(times>k*m)return ;
     }
     return ;
 }
 int main(void){
     scanf("%I64d%I64d%I64d%I64d",&n,&m,&k,&p);
     l=,r=MAX;
     for(LL i=;i<n;++i)
         scanf("%I64d%I64d",&h[i],&a[i]);
     while(l<r){//二分
         if(judge(mid))r=mid;
         else l=mid+;
     }
     printf("%I64d\n",l);
 }