HDU-1757--A Simple Math Problem（矩阵乘法）

Problem Description

Lele now is thinking about a simple function f(x).
If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .
Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.

Input

The problem contains mutiple test cases.Please process to the end of file.
In each case, there will be two lines.
In the first line , there are two positive integers k and m. ( k<2*10^9 , m < 10^5 )
In the second line , there are ten integers represent a0 ~ a9.

Output

For each case, output f(k) % m in one line.

Sample Input

10 9999
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0

Sample Output

45
104

Author

linle

Source

2007省赛集训队练习赛（6）_linle专场

Recommend

lcy

矩阵乘法

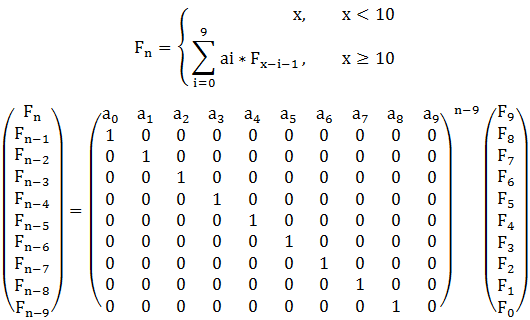
如图所示，可以将递推式写成矩阵形式

类似于将斐波那契数列写成矩阵形式

因为数据量很大，需要用到矩阵快速幂

矩阵快速幂见这篇博客

http://www.cnblogs.com/yan-boy/archive/2012/11/29/2795294.html

需要注意的一个小细节是，在进行乘法（不是矩阵乘法）运算时，注意要模上一个数，防止溢出（因为这个WA了好几发）

代码：

#include<bits/stdc++.h>
using namespace std;
struct  node
{
    int m[10][10];
    node(){
        memset(m,0,sizeof(m));
//        for(int i=0;i<10;i++){
//            for(int j=0;j<10;j++)
//                m[i][j]=0;
//        }
    }
};
    int mod;
node multi(node &a,node &b)
{
    node tmp;
    for(int i=0;i<10;i++){
        for(int j=0;j<10;j++){
            int sum=0;
            for(int k=0;k<10;k++){
                sum+=(a.m[i][k]%mod)*(b.m[k][j]%mod);
            }
            tmp.m[i][j]=sum;
        }
    }
    return tmp;
}
void e_mat(node &a)
{
    for(int i=0;i<10;i++){
        a.m[i][i]=1;
    }
}
node quick_mul(node &a,int n)
{
    node tmp=a;
    //e_mat(tmp);
    node res;
    e_mat(res);
    if(n&1){
        res=a;
    }
    n=n>>1;
    while(n!=0){
        tmp=multi(tmp,tmp);
        if(n&1){
            res=multi(res,tmp);
        }
        n=n>>1;
    }
    return res;
}
void print(node &a)
{
    cout<<"---------------------------"<<endl;
    for(int i=0;i<10;i++){
        cout<<i<<"ÐÐ"<<"\t";
        for(int j=0;j<10;j++){
            cout<<a.m[i][j]<<"\t";
        }
        cout<<endl;
    }
    cout<<"---------------------------"<<endl;
}
int main()
{
    //freopen("data.in","r",stdin);
    int n;

    int ai[11];
    node x;
    for(int i=0;i<10;i++){
        x.m[i][0]=9-i;
    }
    while(~scanf("%d%d",&n,&mod)){
        for(int i=0;i<10;i++){
            scanf("%d",ai+i);
        }
        if(n<10){
            printf("%d\n",n);
            continue;
        }
        node a;
        //print(a);
        for(int i=0;i<10;i++){
            a.m[0][i]=ai[i];
        }
        //print(a);
        for(int i=1;i<10;i++){
            a.m[i][i-1]=1;
        }
        //print(a);
        node res=quick_mul(a,n-9);
        //print(res);
        //print(x);
        res=multi(res,x);
        //print(res);
        printf("%d\n",(res.m[0][0])%mod);
    }
}