【算法设计与分析基础】24、kruskal算法详解

首先我们获取这个图

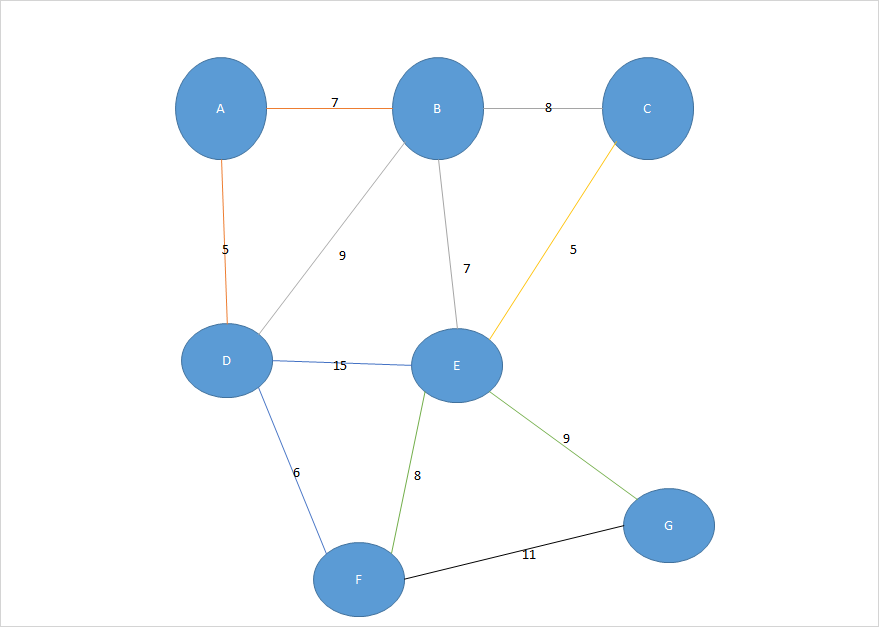
根据这个图我们可以得到对应的二维矩阵图数据

根据kruskal算法的思想，首先提取所有的边，然后把所有的边进行排序

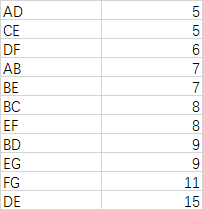
思路就是把这些边按照从小到大的顺序组装，至于如何组装

这里用到并查算法的思路

* 1、makeset(x)，也就是生成单元素集合，也就是每一个节点
* 2、find(x) 返回一个包含x的子集，这个集合可以看成一个有根树
* 3、union(x,y) 构造分别包含x和y的不相交的子集子集Sx和Sy的并集，这里尤为关键：！！！！

了解到这些思路之后，开始我们的算法

第一步：获取这个文件的矩阵数据，存放到对象中

package cn.xf.algorithm.ch09Greedy.vo;
 
import java.io.BufferedInputStream;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.util.ArrayList;
import java.util.List;
 
import org.junit.Test;
 
public class MGraph {
    private int eleSize;
    private int nums[][];
    private List<KruskalBianVo> kruskalBianVos = new ArrayList<KruskalBianVo>();
 
    public MGraph() {
        // TODO Auto-generated constructor stub
    }
 
    public MGraph(int eleSize, int[][] nums) {
        this.eleSize = eleSize;
        this.nums = nums;
    }
 
    public MGraph(File file) throws Exception {
        if(file.exists()) {
          //读取数据流，获取数据源
            FileInputStream fis;
            BufferedInputStream bis;
            try {
                fis = new FileInputStream(file);
                //缓冲
                bis = new BufferedInputStream(fis);
                byte buffer[] = new byte[1024];
                while(bis.read(buffer) != -1) {
                    String allData = new String(buffer);
                    String lines[] = allData.split("\r\n");
                    int allLines = lines.length;
                    int allColumns = lines[0].split(" ").length;
                    if(allLines < allColumns) {
                        //如果行比较小
                        eleSize = allLines;
                    } else {
                        //否则以列为准
                        eleSize = allColumns;
                    }
                    nums = new int[eleSize][eleSize];
                    for(int i = 0; i < eleSize; ++i) {
                        //对每一行数据进行入库处理
                        String everyNums[] = lines[i].split(" ");
                        for(int j = 0; j < eleSize; ++j) {
                            nums[i][j] = Integer.parseInt(everyNums[j]);
                        }
                    }
                }
 
                //获取这个矩阵的所有边  kruskalBianVos
                for(int i = 0; i < eleSize; ++i) {
                    for(int j = i + 1; j < eleSize; ++j) {
                        if(nums[i][j] < 999) {
                            KruskalBianVo kruskalBianVo = new KruskalBianVo();
                            kruskalBianVo.setBeginNode(i);
                            kruskalBianVo.setEndNode(j);
                            kruskalBianVo.setLength(nums[i][j]);
                            kruskalBianVos.add(kruskalBianVo);
                        }
                    }
                }
 
            } catch (FileNotFoundException e) {
                e.printStackTrace();
            }
        } else {
            System.out.println("文件不存在");
        }
    }
 
    public int getEleSize() {
        return eleSize;
    }
    public void setEleSize(int eleSize) {
        this.eleSize = eleSize;
    }
    public int[][] getNums() {
        return nums;
    }
    public void setNums(int[][] nums) {
        this.nums = nums;
    }
 
    public List<KruskalBianVo> getKruskalBianVos() {
        return kruskalBianVos;
    }
 
    public void setKruskalBianVos(List<KruskalBianVo> kruskalBianVos) {
        this.kruskalBianVos = kruskalBianVos;
    }
 
    public static void main(String[] args) {
        String path = MGraph.class.getResource("").getPath();
        path = path.substring(0, path.indexOf("/vo"));
        File f = new File(path + "/resource/test.txt");
        try {
            MGraph mg = new MGraph(f);
            System.out.println(mg.getKruskalBianVos().size());
            int rr[][] = mg.getNums();
            System.out.println(rr);
        } catch (Exception e) {
            e.printStackTrace();
        }
    }
 
}

　　

数据对象：

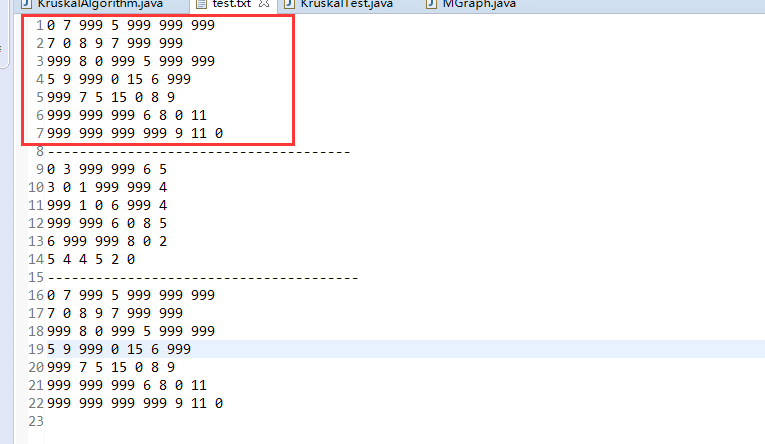
第二步：建立相应的复制类：

存放边数据vo

package cn.xf.algorithm.ch09Greedy.vo;
 
public class KruskalBianVo {
 
	private int beginNode; //开始节点的index
	private int endNode; 	//结束节点的index
	private int length;	//边长
    public int getBeginNode() {
        return beginNode;
    }
    public void setBeginNode(int beginNode) {
        this.beginNode = beginNode;
    }
    public int getEndNode() {
        return endNode;
    }
    public void setEndNode(int endNode) {
        this.endNode = endNode;
    }
    public int getLength() {
        return length;
    }
    public void setLength(int length) {
        this.length = length;
    }
 
}

　　

交换辅助类

package cn.xf.algorithm.ch09Greedy.util;
 
import java.util.List;
 
import cn.xf.algorithm.ch09Greedy.vo.KruskalBianVo;
 
public class Greedy {
 
	public static void swapKruskalBianVo(List<KruskalBianVo> kruskalBianVo, int left, int right) {
		if(kruskalBianVo == null || kruskalBianVo.size() <= 1 || left >= right) {
			return;
		}
 
		//交换节点
		KruskalBianVo kruskalBianVoTemp = kruskalBianVo.get(left);
		kruskalBianVo.set(left, kruskalBianVo.get(right));
		kruskalBianVo.set(right, kruskalBianVoTemp);
	}
}

　　

对边进行快排辅助类

package cn.xf.algorithm.ch09Greedy.util;
 
import java.util.List;
 
import cn.xf.algorithm.ch09Greedy.vo.KruskalBianVo;
 
public class QuikSort {
	//先找中间点
	public static int getMiddlePoint(List<KruskalBianVo> kruskalBianVo, int left, int right, boolean isMinToMax) {
		if(kruskalBianVo == null || kruskalBianVo.size() <= 1 || left >= right) {
			return left;
		}
		//开始快排核心程序，就是对数列两边进行交换
		//1、首选第一个元素作为第一个参照元素
		//2、设置左边向右遍历的起点，设定右边向左遍历的起点
		KruskalBianVo midValue = kruskalBianVo.get(left);
		int leftIndex = left + 1;
		int rightIndex = right;
		int count = 0;
		//循环遍历，知道left跑到right的右边
		while(leftIndex < rightIndex) {
			//确定好区间之后交换位置
			if(isMinToMax) {
				//从小到大
				//遍历左边数据
				while(kruskalBianVo.get(leftIndex).getLength() <= midValue.getLength() && leftIndex < right) {
					++leftIndex;
				}
				//遍历右边数据
				while(kruskalBianVo.get(rightIndex).getLength() > midValue.getLength() && rightIndex > left) {
					--rightIndex;
				}
			} else {
				//如果是从大到小
				//遍历左边数据
				while(kruskalBianVo.get(leftIndex).getLength() > midValue.getLength()) {
					++leftIndex;
				}
				//遍历右边数据
				while(kruskalBianVo.get(rightIndex).getLength() < midValue.getLength()) {
					--rightIndex;
				}
			}
			//交换位置
			Greedy.swapKruskalBianVo(kruskalBianVo, leftIndex, rightIndex);
			++count;
		}
		//最后一次交换之后是不必要的交换，因为已经错开位置了，这里做一个调整
		//交换位置
		if(count > 0) {
			//如果进入过循环，那么肯定进行了一次，交换，那么要撤销那一次的无效
			Greedy.swapKruskalBianVo(kruskalBianVo, leftIndex, rightIndex);
			//吧最开始的位置和中间的位置进行交换
			//交换位置
			Greedy.swapKruskalBianVo(kruskalBianVo, left, rightIndex);
		}
 
		//返回中间位置的索引
		return rightIndex;
	}
 
	public static void sort(List<KruskalBianVo> kruskalBianVo, Boolean isMinToMax) {
		if(kruskalBianVo == null || kruskalBianVo.size() <= 0)
			return;
		if(isMinToMax == null)
			isMinToMax = true;
		sort(kruskalBianVo, 0, kruskalBianVo.size() - 1, isMinToMax);
	}
 
	private static void sort(List<KruskalBianVo> kruskalBianVo, int left, int right, Boolean isMinToMax) {
		if(left < right) {
			//如果左索引小于右索引，那么执行递归
			int mid = getMiddlePoint(kruskalBianVo, left, right, isMinToMax);
			sort(kruskalBianVo, left, mid - 1, isMinToMax);
			sort(kruskalBianVo, mid + 1, right, isMinToMax);
		}
	}
}

　　

存放树节点的tree结构

package cn.xf.algorithm.tree;
 
import java.util.List;
 
/**
 * 树节点
 *
 * .
 *
 * @author xiaof
 * @version Revision 1.0.0
 * @see:
 * @创建日期：2017年8月18日
 * @功能说明：
 *
 */
public class TreeNode {
    private List<TreeNode> nextNodes;
    private Object value;
    private TreeNode parent = null; //指向父节点
    public TreeNode() {
    }
    public TreeNode(List<TreeNode> nextNodes, Object value) {
        this.nextNodes = nextNodes;
        this.value = value;
    }
    public List<TreeNode> getNextNodes() {
        return nextNodes;
    }
    public void setNextNodes(List<TreeNode> nextNodes) {
        this.nextNodes = nextNodes;
    }
    public Object getValue() {
        return value;
    }
    public void setValue(Object value) {
        this.value = value;
    }
	public TreeNode getParent() {
		return parent;
	}
	public void setParent(TreeNode parent) {
		this.parent = parent;
	}
}

　　

最后实现kruskal算法的核心程序

各个节点选中过程图展示

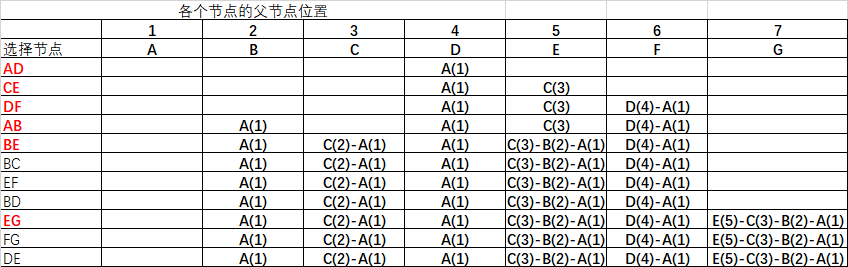
package cn.xf.algorithm.ch09Greedy;
 
import java.util.ArrayList;
import java.util.List;
 
import cn.xf.algorithm.ch09Greedy.util.QuikSort;
import cn.xf.algorithm.ch09Greedy.vo.KruskalBianVo;
import cn.xf.algorithm.ch09Greedy.vo.MGraph;
import cn.xf.algorithm.tree.TreeNode;
 
/**
 * kruskal 算法， 寻找最小生成树
 * 功能： http://blog.csdn.net/luomingjun12315/article/details/47700237\
 *      http://blog.csdn.net/niushuai666/article/details/6689285
 *      http://blog.sina.com.cn/s/blog_a00f56270101a7op.html
 * @author xiaofeng
 * @date 2017年8月21日
 * @fileName KruskalAlgorithm.java
 *
 * 判定回环：判定回环的思路是，如果两个节点联通之后，存在回环，那么两个节点往上遍历这颗树，最终肯定会汇集到根节点，
 * 如果两个节点相连的这根线不存在回环中，那么往上遍历节点，两个节点的根就不会重逢
 * 那么这里有个点
 * 1。这根节点的上级节点存储问题
 * 这里采用数组，也就是V[I]标识I的父节点，这样来存储，当没有改变的时候，也就是没有上级的时候，那么根节点就是本身
 *
 * 2。如何添加节点的父节点
 * 如果这个节点的被修改过了，存在上级节点，那么就把这个a起点作为起点，b作为后续节点
 * 否则，以另一个作为起点
 *
 * 对于是否回环的问题，可以看看，不相交子集和并查算法
 * 其中并查算法：快速求并的思路，分三步实现
 * 1、makeset(x)，也就是生成单元素集合，也就是每一个节点
 * 2、find(x) 返回一个包含x的子集，这个集合可以看成一个有根树
 * 3、union(x,y) 构造分别包含x和y的不相交的子集子集Sx和Sy的并集，这里尤为关键：！！！！
 * ！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！
 * ！  这里快速求并的核心思路是，											                       ！！
 * ！  吧Sy树的根附加到Sx的根上，也就是新子集的根作为X树的根的一个孩子节点附加进入	       ！！
 * ！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！
 */
public class KruskalAlgorithm {
 
    public void kruska(MGraph mg) {
        if(mg == null)
            return;
        //获取图的所有边信息
        List<KruskalBianVo> allBian = mg.getKruskalBianVos();
        //进行排序处理,这里用一个快排
        QuikSort.sort(allBian, true);
        //排序结束之后按照从小到大的顺序进行操作
        int ecounter = 0;
        //为求是否有回环，使用快速求并的方式构造不同的子树
        //1、 makeset 阶段,建立容器，存放森林
        List<TreeNode> allTree = new ArrayList<TreeNode>();
        for(int i = 0; i < mg.getEleSize(); ++i) {
        	TreeNode treeNode = new TreeNode();
        	treeNode.setValue(i); //第i个节点
        	allTree.add(treeNode);
        }
        //根据节点个数，按照A-Z进行设置名字
        char names[] = new char[mg.getEleSize()];
        for(int i = 0; i < mg.getEleSize(); ++i) {
            names[i] = (char) ('A' + i);
        }
 
        //2、find(x)  寻找x节点加入集合中
        int k = 0;
        while(ecounter < mg.getEleSize() && k < allBian.size()) {
        	//获取节点对象
        	KruskalBianVo kruskalBianVo = allBian.get(k);
        	//判断当前边的两个节点加入之后是否有回路
        	int first = kruskalBianVo.getBeginNode();
        	int second = kruskalBianVo.getEndNode();
        	//求并 3、union(x,y)
        	if(union(allTree, first, second)) {
        		//如果顺利加入
        		System.out.println("[" + names[first] + "]=>[" + names[second] + "] 边长为：" + kruskalBianVo.getLength());
        		++ecounter;
        	}
        	++k; // 计数循环
        }
 
    }
 
    /**
     * 判断能否合并的，就是寻找根部父节点是否一致
     * @param allTree
     * @param first
     * @param second
     * @return
     */
    public Boolean union(List<TreeNode> allTree, int first, int second) {
    	TreeNode root1 = getRoot(allTree.get(first));
    	TreeNode root2 = getRoot(allTree.get(second));
    	if(root1 == root2) {
    		return false;
    	} else {
    		//如果不同根，那么把一边的根加入到一边中
    		root2.setParent(root1);
    	}
 
    	return true;
    }
 
    private TreeNode getRoot(TreeNode current) {
		if(current.getParent() == null)
			return current;
		else {
			return getRoot(current.getParent());
		}
	}
 
    /**
     * 孩子节点是否包含
     * @param root
     * @param value
     * @return
     */
    public Boolean haveChild(TreeNode root, Object value) {
    	//判断颗树是否有对应的孩子节点
    	Boolean result = false;
    	if(root.getValue().equals(value)) {
    		return true;
    	} else {
    		for(int i = 0; i < root.getNextNodes().size(); ++i) {
    			//判断孩子节点的孩子。。。是否包含
    			if(haveChild(root.getNextNodes().get(i), value)) {
    				result = true;
    				break;
    			}
    		}
    	}
    	return result;
    }
 
    public Boolean findParent(TreeNode root, Object value) {
    	//判断颗树是否有对应的孩子节点
    	Boolean result = false;
    	if(root.getParent() != null) {
    		//存在父节点
    		if(root.getParent().getValue().equals(value)) {
    			result = true;
    		} else {
    			result = findParent(root.getParent(), value);
    		}
    	}
 
    	return result;
    }
 
}

　　

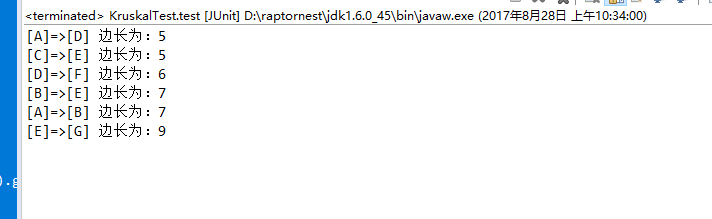
测试结果：

package algorithm.ch09Greedy;
 
import java.io.File;
 
import org.junit.Test;
 
import cn.xf.algorithm.ch09Greedy.KruskalAlgorithm;
import cn.xf.algorithm.ch09Greedy.vo.MGraph;
 
public class KruskalTest {
 
	@Test
	public void test() {
		String path = KruskalTest.class.getResource("").getPath();
//		System.out.println(path);
		File inputFile = new File(path + "/test.txt");
		MGraph mg = null;
		try {
			mg = new MGraph(inputFile);
		} catch (Exception e) {
			e.printStackTrace();
		}
 
		KruskalAlgorithm kruskalAlgorithm = new KruskalAlgorithm();
 
		kruskalAlgorithm.kruska(mg);
 
	}
 
	@Test
	public void test2() {
	    System.out.println('A' - 1);
	}
}

　　

展示：

包结构：