切比雪夫定理(Chebyshev's theorem)与经验法则(Empirical Rule)
切比雪夫定理(Chebyshev's theorem):适用于任何数据集,而不论数据的分布情况如何。
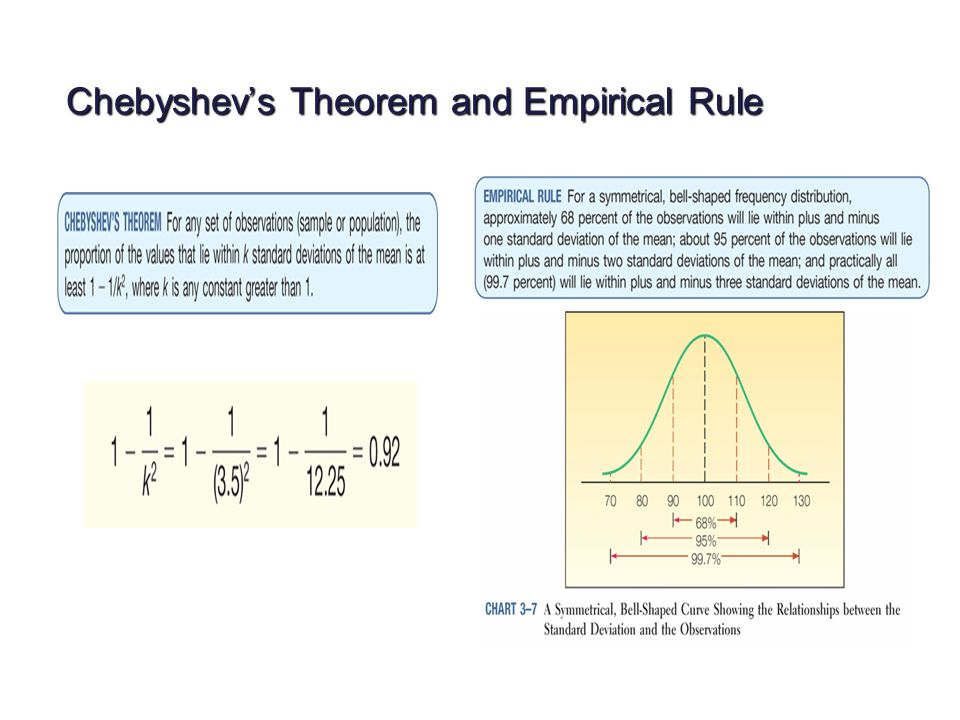
与平均数的距离在z个标准差之内的数值所占的比例至少为(1-1/z2),其中z是大于1的任意实数。
至少75%的数据值与平均数的距离在z=2个标准差之内;
至少89%的数据值与平均数的距离在z=3个标准差之内;
至少94%的数据值与平均数的距离在z=4个标准差之内;
经验法则(Empirical Rule):需要数据符合正态分布。
大约68%的数据值与平均数的距离在1个标准差之内;
大约95%的数据值与平均数的距离在2个标准差之内;
几乎所有的数据值与平均数的距离在3个标准差之内;
切比雪夫定理(Chebyshev's theorem)与经验法则(Empirical Rule)的更多相关文章
- 68.26-95.44-99.74 rule|empirical rule
6.3 Working with Normally Distributed Variables As illustrated in the previous example, the 68.26-95 ...
- 切比雪夫多项式(Chebyshev Polynomials)
切比雪夫多项式在逼近理论中有重要的应用.这是因为第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值.相应的插值多项式能最大限度地降低龙格现象,并且提供多项式在连续函数的最佳一致逼近. 参 ...
- 主定理(Master Theorem)与时间复杂度
1. 问题 Karatsuba 大整数的快速乘积算法的运行时间(时间复杂度的递推关系式)为 T(n)=O(n)+4⋅T(n/2),求其最终的时间复杂度. 2. 主定理的内容 3. 分析 所以根据主定理 ...
- [笔记] 兰道定理 Landau's Theorem
兰道定理的内容: 一个竞赛图强连通的充要条件是:把它的所有顶点按照入度d从小到大排序,对于任意\(k\in [0,n-1]\)都不满足\(\sum_{i=0}^k d_i=\binom{k+1}{2} ...
- 斯托克斯定理(Stokes' theorem)
1. 几种形式 ∮∂SPdx+Qdy+Rdz=∬S∣∣∣∣∣∣cosα∂∂xPcosβ∂∂yQcosγ∂∂zR∣∣∣∣∣∣dS ∮∂Ωw=∬Ωdw 左边是内积: 右边是外积: 物理上的应用: ∮∂SE ...
- Ramsey's_theorem Friendship Theorem 友谊定理
w https://en.wikipedia.org/wiki/Ramsey's_theorem https://zh.wikipedia.org/wiki/拉姆齐定理 在组合数学上,拉姆齐(Rams ...
- (多项式)因式分解定理(Factor theorem)与多项式剩余定理(Polynomial remainder theorem)(多项式长除法)
(多项式的)因式分解定理(factor theorem)是多项式剩余定理的特殊情况,也就是余项为 0 的情形. 0. 多项式长除法(Polynomial long division) Polynomi ...
- 对主定理(Master Theorem)的理解
前言 虽说在学OI的时候学到了非常多的有递归结构的算法或方法,也很清楚他们的复杂度,但更多时候只是能够大概脑补这些方法为什么是这个复杂度,而从未从定理的角度去严格证明他们.因此借着这个机会把主定理整个 ...
- Law of large numbers and Central limit theorem
大数定律 Law of large numbers (LLN) 虽然名字是 Law,但其实是严格证明过的 Theorem weak law of large number (Khinchin's la ...
随机推荐
- NETCore执行Shell修改Centos系统IP信息
原文:NETCore执行Shell修改Centos系统IP信息 目录 shell代码 NETCore执行Shell文件 注意事项 shell代码 首先通过find命令找到/etc/sysconfig/ ...
- phpstorm 2016.3.2 的最新破解方法
v2.0 最新的方式 第一:下载PHPStorm20173.2:(下载链接:windows) 第二:直接用浏览器打开 http://idea.lanyus.com/ ,点击页面中的“获得注册码”,然后 ...
- 第一阶段:Java基础 1.JAVA开发介绍---6. Java基本数据类型
Java 的两大数据类型: 内置数据类型(基本数据类型) 引用数据类型 本数据类型: Java语言提供了八种基本类型.六种数字类型,一种字符类型,还有一种布尔型. byte,short,int,lon ...
- ip2region.jar实现ip转地址
ip转地址 根据ip地址查询出所在地址. GitHub地址 https://github.com/lionsoul2014/ip2region/ pom坐标 <dependency> &l ...
- Golang中文乱码问题
在学习golang读取文件的过程中,遇到中文显示乱码的问题!golang没有自带的编解码包,因此需要借助第三方包 解决方法: 引入第三发转码包:git clone https://github.com ...
- TensorFlow NMT的数据处理过程
在tensorflow/nmt项目中,训练数据和推断数据的输入使用了新的Dataset API,应该是tensorflow 1.2之后引入的API,方便数据的操作.如果你还在使用老的Queue和Coo ...
- java 获取当前方法的被调用信息(被那个方法那个类那一行调用)
public void testMethod(){ Test1 t1 = new Test1(); t1.my(); } public static void main(String[] args) ...
- 随笔记录--Array类型
前言:除了Object类型之外,Array类型恐怕是ECMAScript中最常用的类型了.而且,ECMAScript中数组与其他多数语言中的数组有很大差别,ECMAScript数组中的每一项可以保存任 ...
- python测试开发django-67.templates模板变量取值
前言 django 的模板里面变量取值是通过句点语法来取值,就是一个点(.)符号.取值的对象也可以是字符串,int类型,list列表,字典键值对,也可以是一个类的实例对象. views视图 比如我在 ...
- Shell脚本监控Linux某个后台进程,当进程死掉后重新启动服务,以httpd为例
Shell脚本如下: vim monitor.sh #!/bin/bash while true # 无限循环 flag=`ps -aux |grep "httpd" |grep ...
