Java [Leetcode 204]Count Primes

题目描述：

Description:

Count the number of prime numbers less than a non-negative number, n.

解题思路：

1. Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrimefunction would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better?

2. As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better?

3. Let's write down all of 12's factors:

   2 × 6 = 12
   3 × 4 = 12
   4 × 3 = 12
   6 × 2 = 12
   

   As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n= p × q and since p ≤ q, we could derive that p ≤ √n.

   Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?

4. The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.

   
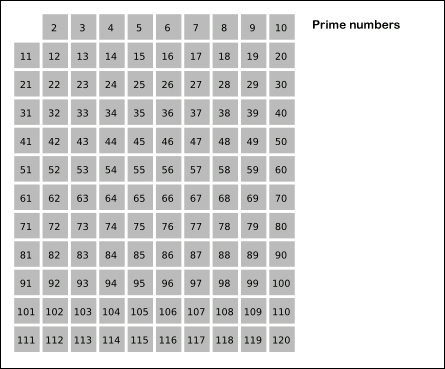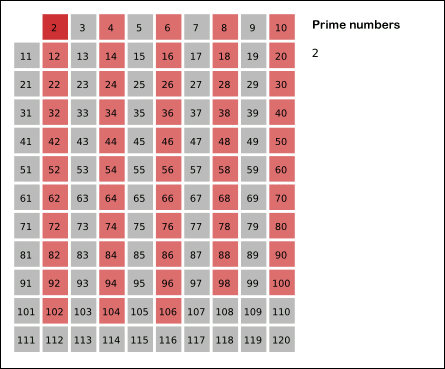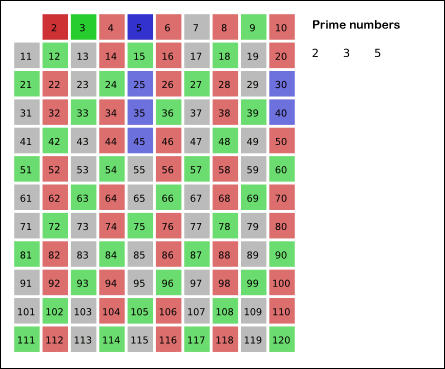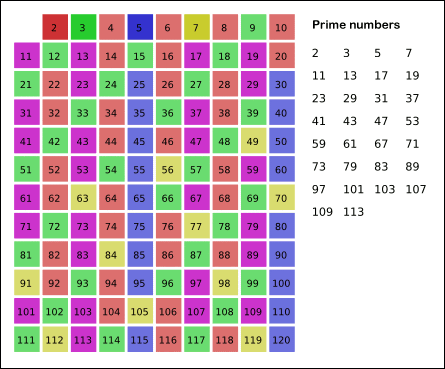
   Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.

   We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well?

5. 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off?

6. In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition?

7. It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3?

8. Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.

   The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.

代码如下：

public class Solution {
    public int countPrimes(int n) {
    	boolean[] isPrime = new boolean[n];
    	int count = 0;
    	for(int i = 2; i < n; i++)
    		isPrime[i] = true;
    	for(int i = 2; i * i < n; i++){
    		if(!isPrime[i])
    			continue;
    		for(int j = i * i; j < n; j += i){
    			isPrime[j] = false;
    		}
    	}
    	for(int i = 2; i < n; i++){
    		if(isPrime[i])
    			count++;
    	}
    	return count;
    }
}