AOV网络拓扑排序
这个算法,主要是为输出一个无环图的拓扑序列
算法思想:
主要依赖一个栈,用来存放没有入度的节点,每次读取栈顶元素,并将栈顶元素的后继节点入度减一,如果再次出现入度为零的节点,就加入到栈中。参考《大话数据结构》,写下下面完整代码,并发现,其中程序的进行,出现错误。v6执行完,应该执行v9,因为此时v9是站顶元素,并不是v0.
算法流程:
int topGraph(graph g){
EdgeNode *e;
int i,k,gettop;
int top = ;
int count = ;
int *stack;
stack = (int *)malloc(g->numVertexes * sizeof(int));
for(i=;i<g->numVertexes;i++){
if(g->headlist[i].in == ) //把入度为0的,即没有入度的点入栈
stack[++top] = i;
}
while(top){
gettop = stack[top--];
printf("%d ",gettop);
count++;
for(e = g->headlist[gettop].fnode; e ; e=e->next){ //一次遍历链表,减少各个子节点的入度
k = e->data;
if(!(--g->headlist[k].in))
stack[++top] = k;
}
}
if(count < g->numVertexes)
return ERROR;
else
return OK;
}
全部代码:
#include <stdio.h>
#include <stdlib.h>
#define MAX 14
#define ERROR 1
#define OK 0
typedef struct edgeNode{
int data;
struct edgeNode *next;
}EdgeNode;
typedef struct headNode{
int in;
int data;
EdgeNode *fnode;
}HeadNode,HeadList[MAX];
typedef struct{
HeadList headlist;
int numEdges,numVertexes;
}Graph,*graph; void initGraph(graph g);
int inputInfo(graph g,int tar,int in,int data,int first);
void printGraph(graph g);
int topGraph(graph g);
int main(){
Graph *g = (Graph *)malloc(sizeof(Graph));
initGraph(g);
printGraph(g); if(topGraph(g) == ERROR)
printf("有环路!\n");
else
printf("没有环路!\n"); free(g);
getchar();
return ;
}
int topGraph(graph g){
EdgeNode *e;
int i,k,gettop;
int top = ;
int count = ;
int *stack;
stack = (int *)malloc(g->numVertexes * sizeof(int));
for(i=;i<g->numVertexes;i++){
if(g->headlist[i].in == ) //把入度为0的,即没有入度的点入栈
stack[++top] = i;
}
while(top){
gettop = stack[top--];
printf("%d ",gettop);
count++;
for(e = g->headlist[gettop].fnode; e ; e=e->next){ //一次遍历链表,减少各个子节点的入度
k = e->data;
if(!(--g->headlist[k].in))
stack[++top] = k;
}
}
if(count < g->numVertexes)
return ERROR;
else
return OK;
}
void printGraph(graph g){
int i;
printf("vertex:%d,edges:%d\n",g->numVertexes,g->numEdges);
EdgeNode *e = (EdgeNode *)malloc(sizeof(EdgeNode));
for(i=;i<MAX;i++){
printf("[in:%d]%d",g->headlist[i].in,g->headlist[i].data);
e = g->headlist[i].fnode;
while(e != NULL){
printf("->%d",e->data);
e = e->next;
}
printf("\n");
}
free(e);
}
void initGraph(graph g){
g->numVertexes = MAX;
g->numEdges = ;
int i;
for(i=;i<MAX;i++){
g->headlist[i].fnode = NULL;
}
inputInfo(g,,,,);
inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,); inputInfo(g,,,,-); inputInfo(g,,,,); inputInfo(g,,,,);
inputInfo(g,,,,); inputInfo(g,,,,); inputInfo(g,,,,-); inputInfo(g,,,,); inputInfo(g,,,,-);
}
int inputInfo(graph g,int tar,int in,int data,int first){
g->numEdges++; if(first == -){ //没有后继的边节点
g->headlist[tar].in = in;
g->headlist[tar].data = data;
return ;
} if(!g->headlist[tar].fnode){ //观察是否已经初始化
g->headlist[tar].in = in;
g->headlist[tar].data = data;
}
EdgeNode *e = (EdgeNode *)malloc(sizeof(EdgeNode));
e->data = first;
e->next = g->headlist[tar].fnode;
g->headlist[tar].fnode = e;
return ;
}
执行示例:
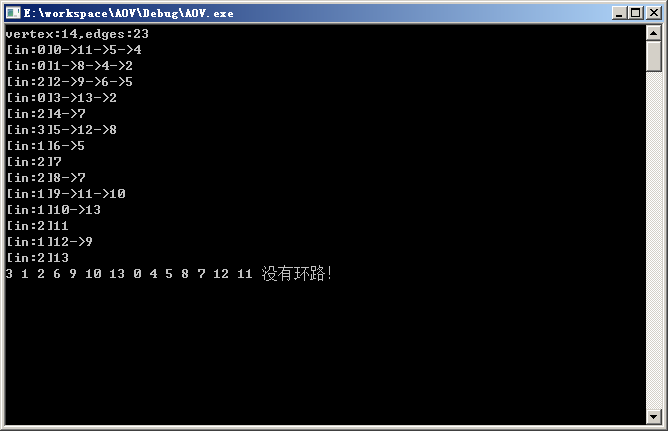
AOV网络拓扑排序的更多相关文章
- AOV拓扑排序实验总结-1
AOV拓扑排序实验总结-1 实验数据:1.实验输入数据在input.txt文件中2.对于n是指有顶点n个,数据的结束标志是一行0 0. 实验目的:获取优秀的AOV排序算法模板 数据结构安排 ...
- AOV拓扑排序实验-2-AOV类的实现
下面是这个类的实现代码: //这只是一个基本的框架,没有封装 #include<iostream> #include<cstdio> #include<malloc.h& ...
- 设计AOV网拓扑排序的算法
拓扑排序 对一个有向图构造拓扑序列的过程称为拓扑排序(不唯一) 思想 从AOV网选择一个没有前驱的顶点并输出 从AOV网中删去该顶点,并且删去所有以该顶点为尾的弧 重复上述两步,直到全部顶点都被输出, ...
- [SOJ] Ordering Tasks
1940. Ordering Tasks Constraints Time Limit: 1 secs, Memory Limit: 32 MB Description John has n task ...
- Hadoop 基石HDFS 一文了解文件存储系统
@ 目录 前言:浅谈Hadoop Hadoop的发展历程 1.1 Hadoop产生背景 1.引入HDFS设计 1.1 HDFS主要特性 2.HDFS体系结构 HDFS工作流程机制 1.各个节点是如何互 ...
- 算法与数据结构(七) AOV网的拓扑排序
今天博客的内容依然与图有关,今天博客的主题是关于拓扑排序的.拓扑排序是基于AOV网的,关于AOV网的概念,我想引用下方这句话来介绍: AOV网:在现代化管理中,人们常用有向图来描述和分析一项工程的计划 ...
- 有向无环图的应用—AOV网 和 拓扑排序
有向无环图:无环的有向图,简称 DAG (Directed Acycline Graph) 图. 一个有向图的生成树是一个有向树,一个非连通有向图的若干强连通分量生成若干有向树,这些有向数形成生成森林 ...
- AOV网络和Kahn算法拓扑排序
1.AOV与DAG 活动网络可以用来描述生产计划.施工过程.生产流程.程序流程等工程中各子工程的安排问题. 一般一个工程可以分成若干个子工程,这些子工程称为活动(Activity).完成了这些活动 ...
- 算法与数据结构(七) AOV网的拓扑排序(Swift版)
今天博客的内容依然与图有关,今天博客的主题是关于拓扑排序的.拓扑排序是基于AOV网的,关于AOV网的概念,我想引用下方这句话来介绍: AOV网:在现代化管理中,人们常用有向图来描述和分析一项工程的计划 ...
随机推荐
- 实现一个简单的FTP服务器(十四)
此为一个网络编程的一个系列,后续会把内容补上...
- VS2010安装中遇到的错误
背景 用win7 64位系统安装VS2010遇到一个错误,网上查了各种资料也没有找到这种解决办法,后来自己找到了解决办法,分享一下,让他人少走一些弯路. 错误信息 安装过程中遇到如下错误: [08/2 ...
- 省常中模拟 Test1 Day1
临洮巨人 排序 题意:在字符串中找出 A.B.C 三个字母出现次数相同的区间个数. 初步的解法是前缀和,用 a(i), b(i), c(i) 表示在位置 i 之前(包括 i)各有 字母 A.B.C 多 ...
- LINUX启动ORACLE监听和服务
可通过secureCRT或者telnet直接连 启动监听命令:lsnrctl start 成功启动后:sqlplus /nolog 回车 conn / as sysdba 回车 startup 回车 ...
- <三>面向对象分析之UML核心元素之参与者
一:版型 --->在UML里有一个概念叫版型.有些书里也称类型,构造型. --->这个概念是对一个UML元素基础定义的扩展.在同一个元素基础定义的基础上赋予特别 ...
- Java与WCF交互(一)补充:用WSImport生成WSDL的Java客户端代码
在<Java与WCF交互(一):Java客户端调用WCF服务>一 文中,我描述了用axis2的一个Eclipse控件生成WCF的Java客户端代理类,后来有朋友建议用Xfire.CXF,一 ...
- Github 终于开始认真考虑开源项目许可证了
如今GitHub已成为全球最流行的开源项目托管平台,但也有质疑声音——“Github中的大多数项目并不算是开源项目”.这是因为Github中大多数项目并没有明确声明所使用的许可证. 根据版权法规定,如 ...
- POJ 1068 Parencodings
Parencodings Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 24932 Accepted: 14695 De ...
- Android WindowManager 监听返回键及home键
一.监听home键盘,Android Home键系统负责监听,捕获后系统自动处理.有时候,我们需要监听home键处理自己的逻辑,监听方法如下: /** * 监听home键广播 */ private f ...
- acdream 1056 (黑白染色)
题意:给你一些关系,每个关系是两只马的名字,表示这两个马不能在一个分组里,问你能否将这些马分成两组. 黑白染色,相邻的点染不同颜色.bfs搞即可,水题. /* * this code is made ...
