python(3)-集合

集合就是把不同的元素组织在一起，但在集合中不允许有重复的元素。

>>> a = set()             #创建集合
>>> type(a)
<class 'set'>

集合中不允许出现重复的元素

>>> a.add('jack')         #向集合中添加元素
>>> print(a)
{'jack'}
>>> a.add("jack")       #再次向集合中添加同样的元素
>>> print(a)
{'jack'}                         #同样的元素只能出现一次

集合的访问：

因为集合是无序的，所以不能对它进行切片，只能遍历，in 或 not in 等方法

>>> s = set("fjihutiejhgir")
>>> print(s)
{'u', 'h', 'i', 'e', 'g', 'j', 't', 'r', 'f'}
>>> a in s
False
>>> a not in s
True
>>> for i in s:
...   print(i)
...
u
h
i
e
g
j
t
r
f
>>>

向集合添加元素，删除元素

>>> s = set("a")
>>> s.update("b")           #添加元素
>>> print(s)
{'b', 'a'}
>>> s.add("c")               #添加元素
>>> print(s)
{'b', 'a', 'c'}
>>> s.remove("a")         #删除元素
>>> print(s)
{'b', 'c'}
>>>

清空集合元素及删除集合

>>> s.clear()
>>> print(s)
set()
>>> del s
>>> print(s)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 's' is not defined

下面重温一下并集，交集，差集的概念

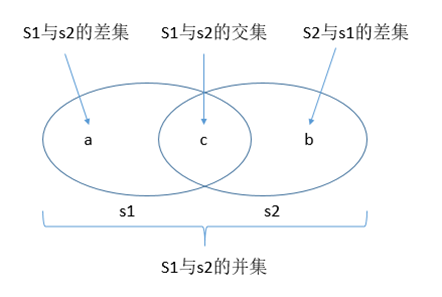
差集，difference()  返回一个新集合

>>> s1 = set("abcdefg")
>>> s2 = set("efghijk")
>>> s1.difference(s2)            #s1与s2的差集
{'b', 'a', 'd', 'c'}
>>> s2.difference(s1)            #s2与s1的差集
{'j', 'h', 'i', 'k'}

交集，&  或　intersection() 返回一个新集合

>>> s1&s2
{'g', 'f', 'e'}
>>> s3 = s1&s2
>>> print(s3)
{'g', 'f', 'e'}
>>> s4 = s1.intersection(s2)
>>> print(s4)
{'g', 'f', 'e'}
>>>

并集， | 或 union()  返回一个新集合

>>> s3 = s1|s2
>>> print(s3)
{'h', 'a', 'd', 'e', 'i', 'k', 'g', 'b', 'j', 'f', 'c'}
>>> s4 = s1.union(s2)
>>> print(s4)
{'h', 'a', 'd', 'e', 'i', 'k', 'g', 'b', 'j', 'f', 'c'}

集合是不能相加，但可以相减

>>> s1-s2
{'b', 'a', 'd', 'c'}
>>> s3 = s1+s2
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for +: 'set' and 'set'

集合之间的and , or

>>> s1 = set("abc")
>>> s2 = set("cde")
>>> s1 and s2           #取s2
{'c', 'd', 'e'}
>>> s1 or s2             #取s1
{'b', 'a', 'c'}

difference_update()    传什么进来就删除什么

>>> s1 = set("abcdefg")
>>> s1.difference_update("a")
>>> print(s1)
{'d', 'e', 'g', 'b', 'f', 'c'}

intersection_update()    还是看例子吧，好理解

>>> s1 = set("abcdefg")
>>> s2 = set("efghij")
>>> s1.intersection_update(s2)          #在s1中只保留s1和s2中都有的元素
>>> print(s1)
{'g', 'f', 'e'}

pop()    在集合中随机删除一个元素并返回该元素，此方法不能带参数

>>> s1.pop("a")
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: pop() takes no arguments (1 given)
>>> s1.pop()
'a'
>>> s1.pop()
'd'

s1.symmetric_difference(s2)    #取出两边的差集

>>> s1 = set("abcdefg")
>>> s2 = set("efghij")
>>> s1.symmetric_difference(s2)
{'j', 'h', 'b', 'a', 'd', 'c', 'i'}

最觉的应用，便是去除重复的元素

>>> li = [1,1,2,2,3,3,4,4,5,5,6,6]
>>> print(set(li))
{1, 2, 3, 4, 5, 6}