【BZOJ3122】[Sdoi2013]随机数生成器 BSGS+exgcd+特判

【BZOJ3122】[Sdoi2013]随机数生成器

Description

Input

输入含有多组数据，第一行一个正整数T，表示这个测试点内的数据组数。  
 
接下来T行，每行有五个整数p，a，b，X1，t，表示一组数据。保证X1和t都是合法的页码。

注意：P一定为质数

Output

共T行，每行一个整数表示他最早读到第t页是哪一天。如果他永远不会读到第t页，输出-1。

Sample Input

3
7 1 1 3 3
7 2 2 2 0
7 2 2 2 1

Sample Output

1
3
-1

HINT

0<=a<=P-1,0<=b<=P-1,2<=P<=10^9

题解：又一道特判神题~

若A=0，直接判；若A=1，用exgcd求；若A>1，此时要用到高中数学的知识。

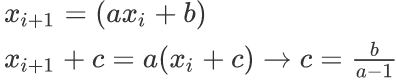
此时xi+c变成了等比数列

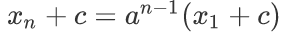
然后上BSGS就行了

#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
#include <map>
using namespace std;
typedef long long ll;
map<ll,ll> mp;
ll pm(ll x,ll y,ll z)
{
	ll ret=1;
	while(y)
	{
		if(y&1)	ret=ret*x%z;
		x=x*x%z,y>>=1;
	}
	return ret;
}
ll solve(ll A,ll B,ll P)
{
	if(!A&&!B)	return 0;
	if(!A)	return -1;
	ll i,x,y,m;
	mp.clear(),mp[B]=0,m=ceil(sqrt(P));
	for(x=1,i=1;i<=m;i++)	x=x*A%P,mp[x*B%P]=i;
	for(y=1,i=1;i<=m;i++)
	{
		y=y*x%P;
		if(mp.find(y)!=mp.end())	return i*m-mp[y];
	}
	return -1;
}
ll exgcd(ll a,ll b,ll &x,ll &y)
{
	if(b==0){x=1,y=0;	return a;}
	ll tmp=exgcd(b,a%b,x,y),t=x;
	x=y,y=t-a/b*x;
	return tmp;
}
int main()
{
	ll T,A,B,P,X,t,tmp,xx,yy;
	scanf("%lld",&T);
	while(T--)
	{
		scanf("%lld%lld%lld%lld%lld",&P,&A,&B,&X,&t);
		if(X==t)
		{
			printf("1\n");
			continue;
		}
		if(A==0)
		{
			if(B==t)	printf("2\n");
			else	printf("-1\n");
			continue;
		}
		if(A==1)
		{
			if(B==0)
			{
				printf("-1\n");
				continue;
			}
			ll g=exgcd(B,P,xx,yy),C=t+B-X;
			if(C%g)
			{
				printf("-1\n");
				continue;
			}
			C/=g,P/=g,xx=xx*C%P;
			if(xx<=0)	xx+=P;
			printf("%lld\n",xx);
			continue;
		}
		tmp=solve(A,((A-1)*t+B)%P*pm(((A-1)*X+B)%P,P-2,P)%P,P)+1;
		if(!tmp)	printf("-1\n");
		else	printf("%lld\n",tmp);
	}
	return 0;
}