深度可分卷积（Depthwise Separable Conv.）计算量分析

上次读到深度可分卷积还是去年暑假，各种细节都有些忘了。记录一下，特别是计算量的分析过程。

1. 标准卷积和深度可分卷积

标准卷积（MobileNet论文中称为Standard Convolution，如下图所示）将N个大小（边长）为\(D_{k}\)、通道数为M的卷积核作用于大小为\(D_{f}\)、通道数同为M的特征图上，最后得到大小为Dp、通道数为N的输出。即标准卷积的每个卷积和的通道数需要与输入特征图的通道数相同，且输出特征图的通道数等于卷积核的个数。(~~以上均为保证文章完整性的废话~~)

深度可分卷积（Depthwise Separable Convolution）其实就是将标准的卷积分为两部分:

第一部分是对输入的特征图的每一个通道单独做卷积，因此这里的卷积核通道数自然也都是1，卷积核的大小仍为\(D_{k}\)，这部分称为Depthwise Convolution
第二部分是对第一部分得到的M个特征图做1 x 1卷积，卷积核个数为N，因此最后的输出同样是\(D_{p}^2 \cdot N\)，这部分称为Pointwise Convolution

举个简单的例子说明，假设我们有一个输入图片，这个输入图片的维度是11 x 11 x 3，标准卷积为3 x 3 x 3 x 6（假设stride为2，padding为1），那么可以得到输出为6 × 6 × 16（6 = (11-3+2*1)/2+1）的输出结果。现在输入图片不变，先通过一个维度是3 × 3 × 1 × 3的深度卷积（输入是3通道，这里有3个卷积核分别作用在3个通道上），得到6 × 6 × 3的中间输出，然后再通过一个维度是1 × 1 × 3 ×16的1 ×1卷积，同样得到输出为6 × 6 × 16。

2. 计算量分析

标准卷积的计算量
记得第一次跟着论文算时，一直盯着输入特征图和卷积核，这样还要考虑padding、stride等等，实际算起来很麻烦。其实只要换个思路，先看输出特征图和卷积核，因为输出特征图中的每一层的每个像素都是一次卷积的结果，因此每次卷积的计算量为：\(D_{k}^2 \cdot M\)，每个卷积核的计算量为： \(D_{p}^2 \cdot D_{k}^2 \cdot M\)，一共N个卷积核，所以总计算量为：\(D_{p}^2 \cdot D_{k}^2 \cdot M \cdot N\)

深度可分卷积的计算量
如下图，Depthwise卷积的计算量为：\(D_{p}^2 \cdot D_{k}^2 \cdot M\)

如下图，Pointwise卷积的计算量为：\(D_{p}^2 \cdot M \cdot N\)

所以，在输入、输出特征图、卷积核大小不变的情况下，深度可分卷积的计算量为标准卷积的：
\[\cfrac{D_{p}^2 \cdot D_{k}^2 \cdot M + D_{p}^2 \cdot M \cdot N}{D_{p}^2 \cdot D_{k}^2 \cdot M \cdot N} = \cfrac{1}{N} + \cfrac{1}{D_{k}^2}\]

因为所有的输出特征图大小均为\(D_{p}\)，即每次卷积的次数相同。在上式中分子分母同时除以\(D_{p}^2\)，得到：\(\cfrac{D_{k}^2 \cdot M + M \cdot N}{D_{k}^2 \cdot M \cdot N}\)，刚好分别是深度可分卷积和标准卷积的参数量。

3. 原理分析

深度可分卷积默认一个假设，即标准卷积核在特征图的通道维度映射中，存在一种类似线性组合的分解特性。标准卷积核需要同时学习空间上的相关性和通道间的相关性，深度可分卷积将这两种相关性显式地分离开来，从上面的图中也能看出，深度可分卷积其实是将标准卷积分为空间（Depthwise）的卷积和通道（Pointwise）的卷积（这个和Xception很类似，MobileNet论文还引用了Xception，但是说两篇文章的目的不一样，MobileNet对可分卷积带来的效率与空间节省方面的好处更感兴趣，而Xception更纠结于根据可分卷积设计出来的网络是否具备很好的准确性。~~反正我是不清楚MobileNet咋投出去了的~~，我佛了，居然是相互引用，好像还是MobileNet在前）。我们用\(K\)表示一个标准卷积核，则：
\[K=M \cdot \Lambda(b) \tag{1}\]
其中，"\(\cdot\)"表示一种特殊的矩阵乘法，其运算法则参考(3)式，b是一个m维矩阵”向量”(Matrix Spaces)，它的每个元素(element)是一个\(s \times s\)大小的2维卷积核：
\[b_{i}=
\left[
\begin{matrix}
b_{11}^i & \cdots & b_{1s}^i \\
\vdots & \ddots & \vdots \\
b_{s1}^i & \cdots & b_{ss}^i
\end{matrix}
\right]
\]
\(\Lambda(b)\)表示\(b_{i}\)为对角元素的对角阵，即：
\[\Lambda(b)=
\left[
\begin{matrix}
b_{1} & 0 & \cdots & 0 \\
0 & b_{2} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & b_{m}
\end{matrix}
\right]
\tag{2}
\]
而\(M\)是一个\(n \times m\)的数值矩阵，n行数表示输出特征图的维度(output channels number)，m表示输入特征图的维度(input channels number)。为了直观，把式(1)写下面的形式：
\[
\left[
\begin{matrix}
k_{11} & \cdots & k_{1m} \\
\vdots & \ddots & \vdots \\
k_{n1} & \cdots & k_{nm}
\end{matrix}
\right]=
\left[
\begin{matrix}
\mu_{11}b_{1} & \cdots & \mu_{1m}b_{m} \\
\vdots & \ddots & \vdots \\
\mu_{n1}b_{1} & \cdots & \mu_{nm}b_{m}
\end{matrix}
\right]=
\left[
\begin{matrix}
\mu_{11} & \cdots & \mu_{1m} \\
\vdots & \ddots & \vdots \\
\mu_{n1} & \cdots & \mu_{nm}
\end{matrix}
\right] \cdot
\left[
\begin{matrix}
b_{1} & \cdots & 0 \\
\vdots & \ddots & \vdots \\
0 & \cdots & b_{m}
\end{matrix}
\right]
\tag{3}
\]
其中，\(k_{ij}=\mu_{ij}b_{j}\)是一个\(s \times s\)的数值矩阵，表示4维常规卷积核中的一个2维小卷积核。然后，利用式(3)来分析模型参数量的压缩程度，可以得到压缩率为：
\[
\cfrac{s \times s \times m + n \times m}{s \times s \times n \times m}=
\cfrac{1}{n}+\cfrac{1}{s \times s}
\]

容易发现，这个结果跟论文中计算量减少率是一样，因为MobileNet从本质上就是基于这种核分解假设而设计的。

关于上述分析的思考
开始看到这个分解的时候感觉很巧妙，但是仔细思考之后又感觉有点问题。

因为在(3)式中，从第1个矩阵（记为X）到第2个矩阵（记为Y），以X的第1列为例，这一列的每一个元素\(k_{i1}\)在Y中都被表示为 \(\mu_{i1}b_{1}\)，\(i\in[1,n]\)。而根据下面参数量的分析，\(n \times m\)指的就是(3)式中的第3个矩阵，这样，\(\mu_{i1}\)都是数，而\(b_{1}\)都是矩阵，可以推出这一列的每个元素都线性相关，即X的第1列中每个元素都线性相关，以此类推，X第2、3...m列中的每个元素都分别线性相关。

X为4维标准卷积核（4维分别是卷积核的宽、高、通道数和个数），所以X的每一行表示一个卷积核（一个4维标准卷积核包含n个3维卷积核），从1到m表示这个卷积核的m个通道；而每一列则表示n个3维卷积核的相同通道；X的每个元素都表示一个2维卷积。按照上一段的分析，X每一列中的元素都分别线性相关，所以可以得出要满足这种分解，1到n这n个3维卷积核对应通道都线性相关。这样的话，那不是无形中给标准卷积转换到深度可分卷积添加了条件，只有满足这种条件的标准卷积才能进行分解？而这也与实验中的事实不符。

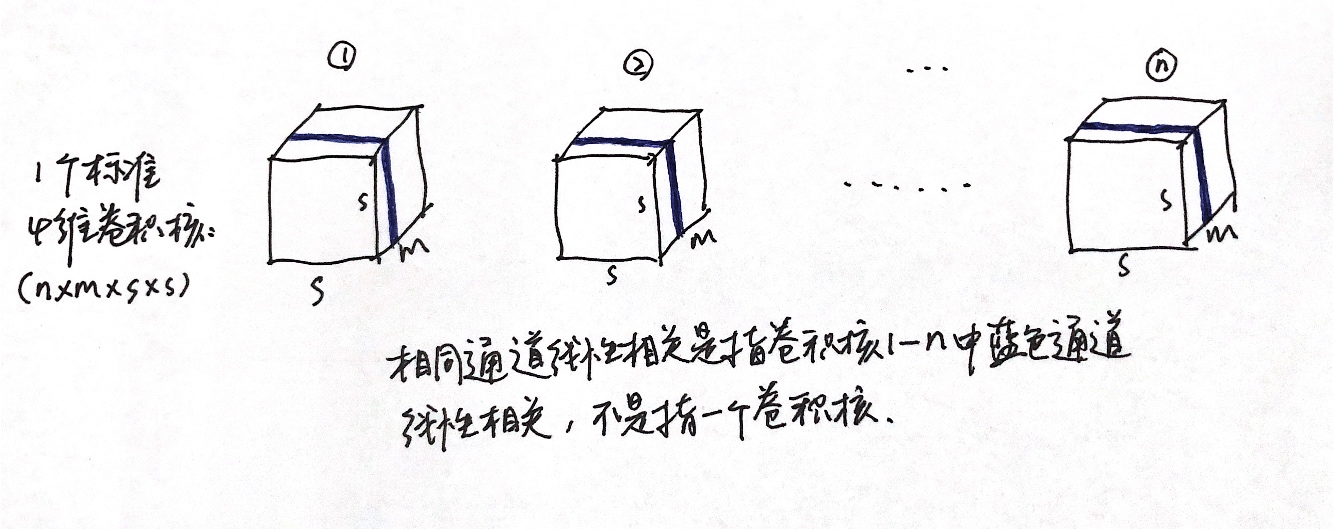
所以我有点疑惑，是我理解有误还是作者（参考4）的这种矩阵分解的解释有问题？搜了一下这个矩阵分解的解释，都是引用的（参考4）。在评论区和作者讨论之后，感觉他没理解我的意思（确实不好表达），所以没好意思继续问下去（一写又是一大堆）。暂时先放一放了，如果有人看到这篇博客，欢迎和我讨论。

参考: