loj #2510. 「AHOI / HNOI2018」道路

#2510. 「AHOI / HNOI2018」道路

题目描述

W 国的交通呈一棵树的形状。W 国一共有 n−1 个城市和 nnn 个乡村，其中城市从 111 到 n−1 编号，乡村从 111 到 nnn 编号，且 111 号城市是首都。道路都是单向的，本题中我们只考虑从乡村通往首都的道路网络。对于每一个城市，恰有一条公路和一条铁路通向这座城市。对于城市 iii，通向该城市的道路（公路或铁路）的起点，要么是一个乡村，要么是一个编号比 iii 大的城市。没有道路通向任何乡村。除了首都以外，从任何城市或乡村出发只有一条道路；首都没有往 外的道路。从任何乡村出发，沿着唯一往外的道路走，总可以到达首都。

W 国的国王小 W 获得了一笔资金，他决定用这笔资金来改善交通。由于资金有限，小 W 只能翻修 n−1 条道路。小 W 决定对每个城市翻修恰好一条通向它的道路，即从公路和铁路中选择一条并进行翻修。小 W 希望从乡村通向城市可以尽可能地便利，于是根据人口调查的数据，小 W 对每个乡村制定了三个参数，编号为 iii 的乡村的三个参数是 aia_ia​i​​，bib_ib​i​​ 和 cic_ic​i​​。假设从编号为 iii 的乡村走到首都一共需要经过 xxx 条未翻修的公路与 yyy 条未翻修的铁路，那么该乡村的不便利值为

ci⋅(ai+x)⋅(bi+y)c_i \cdot (ai + x) \cdot (bi + y)c​i​​⋅(ai+x)⋅(bi+y)

在给定的翻修方案下，每个乡村的不便利值相加的和为该翻修方案的不便利值。

翻修 n−1 条道路有很多方案，其中不便利值最小的方案称为最优翻修方案，小 W 自然希望找到最优翻修方案，请你帮助他求出这个最优翻修方案的不便利值。

输入格式

第一行为正整数 nnn。 接下来 n−1 行，每行描述一个城市。其中第 iii 行包含两个数 si,tis_i, t_is​i​​,t​i​​。sis_is​i​​ 表示通向第 iii 座城市的公路的起点，tit_it​i​​ 表示通向第 iii 座城市的铁路的起点。如果 si>0s_i > 0s​i​​>0，那么存在一条从第 sis_is​i​​ 座城市通往第 iii 座城市的公路，否则存在一条从第 −si-s_i−s​i​​ 个乡村通往第 iii 座城市的公路；tit_it​i​​ 类似地，如果 ti>0t_i > 0t​i​​>0，那么存在一条从第 tit_it​i​​ 座城市通往第 iii 座城市的铁路，否则存在一条从第 −ti-t_i−t​i​​ 个乡村通往第 iii 座城市的铁路。

接下来 nnn 行，每行描述一个乡村。其中第 iii 行包含三个数 ai,bi,cia_i, b_i, c_ia​i​​,b​i​​,c​i​​，其意义如题面所示。

输出格式

输出一行一个整数，表示最优翻修方案的不便利值。

样例

样例输入 1

6
2 3
4 5
-1 -2
-3 -4
-5 -6
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

样例输出 1

54

样例解释 1

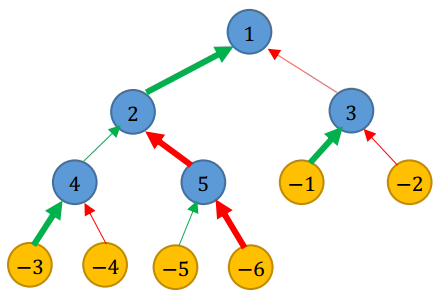
如图所示，我们分别用蓝色、黄色节点表示城市、乡村；用绿色、红色箭头分别表示公路、铁路；用加粗箭头表示翻修的道路。

一种不便利值等于 545454 的方法是：翻修通往城市 222 和城市 555 的铁路，以及通往其他城市的公路。用→\rightarrow→和⇒\Rightarrow⇒表示公路和铁路，用∗→和∗⇒表示翻修的公路和铁路，那么：

• 编号为 111 的乡村到达首都的路线为：−1∗→3⇒1，经过 000 条未翻修公路和 111 条未翻修铁路，代价为 3×(1+0)×(2+1)=93 \times (1 + 0) \times (2 + 1) = 93×(1+0)×(2+1)=9；
• 编号为 222 的乡村到达首都的路线为：−2⇒3⇒1，经过 000 条未翻修公路和 222 条未翻修铁路，代价为 2×(1+0)×(3+2)=102 \times (1 + 0) \times (3 + 2) = 102×(1+0)×(3+2)=10；
• 编号为 333 的乡村到达首都的路线为：−3∗→4→2∗→1，经过 111 条未翻修公路和 000 条未翻修铁路，代价为 3×(2+1)×(1+0)=93 \times (2 + 1) \times (1 + 0) = 93×(2+1)×(1+0)=9；
• 编号为 444 的乡村到达首都的路线为：−4⇒4→2∗→1，经过 111 条未翻修公路和 111 条未翻修铁路，代价为 1×(2+1)×(3+1)=121 \times (2 + 1) \times (3 + 1) = 121×(2+1)×(3+1)=12；
• 编号为 555 的乡村到达首都的路线为：−5→5∗⇒2∗→1，经过 111 条未翻修公路和 000 条未翻修铁路，代价为 2×(3+1)×(1+0)=82 \times (3 + 1) \times (1 + 0) = 82×(3+1)×(1+0)=8；
• 编号为 666 的乡村到达首都的路线为：−6∗⇒5∗⇒2∗→1，经过 000 条未翻修公路和 000 条未翻修铁路，代价为 1×(3+0)×(2+0)=61 \times (3 + 0) \times (2 + 0) = 61×(3+0)×(2+0)=6；

总的不便利值为 9+10+9+12+8+6=549 + 10 + 9 + 12 + 8 + 6 = 549+10+9+12+8+6=54。可以证明这是本数据的最优解。

样例输入 2

9
2 -2
3 -3
4 -4
5 -5
6 -6
7 -7
8 -8
-1 -9
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1

样例输出 2

548

样例解释 2

在这个样例中，显然应该翻修所有公路。

样例输入 3

12
2 4
5 3
-7 10
11 9
-1 6
8 7
-6 -10
-9 -4
-12 -5
-2 -3
-8 -11
53 26 491
24 58 190
17 37 356
15 51 997
30 19 398
3 45 27
52 55 838
16 18 931
58 24 212
43 25 198
54 15 172
34 5 524

样例输出 3

5744902

数据范围与提示

共 202020 组数据，编号为 1∼20。

对于编号 ≤4\le 4≤4 的数据，n≤20n \le 20n≤20；

对于编号为 5∼8 的数据，ai,bi,ci≤5，n≤50；

对于编号为 9∼12 的数据，n≤2000n \le 2000n≤2000；

对于所有的数据，n≤20000n \le 20000n≤20000，1≤ai,bi≤601 \le a_i, b_i \le 601≤a​i​​,b​i​​≤60，1≤ci≤1091 \le c_i \le 10^91≤c​i​​≤10​9​​，si,tis_i, t_is​i​​,t​i​​ 是 [−n,−1]∩(i,n−1] 内的整数，任意乡村可以通过不超过 404040 条道路到达首都。

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 50
using namespace std;
int map[maxn][maxn];
int n,m,head[maxn],num,a[maxn],b[maxn],c[maxn],son[maxn][];
struct node{int to,pre,v,w;}e[maxn*maxn];
void Insert(int from,int to,int w){
    e[++num].to=to;
    e[num].w=w;
    e[num].pre=head[from];
    head[from]=num;
}
int cnt[maxn][];
long long ans=;
void dfs(int x,int cnt0,int cnt1){
    if(x<=n){
        cnt[x][]=cnt0;
        cnt[x][]=cnt1;
    }
    for(int i=head[x];i;i=e[i].pre){
        int to=e[i].to;
        if(e[i].w==&&e[i].v==)dfs(to,cnt0+,cnt1);
        else if(e[i].w==&&e[i].v==)dfs(to,cnt0,cnt1+);
        else dfs(to,cnt0,cnt1);
    }
}
long long count(int sta){
    for(int i=;i<n;i++){
        if(sta&(<<(i-))){//连向右孩子的边被重建
            e[map[i+n][son[i+n][]]].v=;
            e[map[i+n][son[i+n][]]].v=;
        }
        else {//连向左孩子的边被重建
            e[map[i+n][son[i+n][]]].v=;
            e[map[i+n][son[i+n][]]].v=;
        }
    }
    dfs(n+,,);
    long long res=;
    for(int i=;i<=n;i++){
        res+=1LL*c[i]*(a[i]+cnt[i][])*(b[i]+cnt[i][]);
    }
    return res;
}
int main(){
    scanf("%d",&n);
    m=n+n-;
    int x,y;
    for(int i=;i<n;i++){
        scanf("%d%d",&x,&y);
        if(x<)x=-x;
        else x+=n;
        if(y<)y=-y;
        else y+=n;
        son[i+n][]=x;son[i+n][]=y;
        Insert(i+n,x,);map[i+n][x]=map[x][i+n]=num;
        Insert(i+n,y,);map[i+n][y]=map[y][i+n]=num;
    }
    for(int i=;i<=n;i++)scanf("%d%d%d",&a[i],&b[i],&c[i]);
    for(int i=;i<(<<(n-));i++){
        ans=min(ans,count(i));
    }
    cout<<ans<<endl;
    return ;
}

20分 暴力

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 20010
using namespace std;
int n,son[maxn][];
long long f[maxn][][];
struct node{long long x,y,z;}a[maxn];
long long dfs(int x,int p,int q){
    if(x>=n){
        int now=x-n+;
        return a[now].z*(a[now].x+p)*(a[now].y+q);
    }
    if(f[x][p][q]!=f[n+][][])return f[x][p][q];
    return f[x][p][q]=min(dfs(son[x][],p,q)+dfs(son[x][],p,q+),dfs(son[x][],p,q)+dfs(son[x][],p+,q));
}
int main(){
    int x,y;
    scanf("%d",&n);
    memset(f,,sizeof(f));
    for(int i=;i<n;i++){
        scanf("%d%d",&x,&y);
        if(x<)x=-x+n-;
        if(y<)y=-y+n-;
        son[i][]=x;
        son[i][]=y;
    }
    for(int i=;i<=n;i++)
        scanf("%lld%lld%lld",&a[i].x,&a[i].y,&a[i].z);
    printf("%lld\n",dfs(,,));
    return ;
}

100分 树形dp