hiho 毁灭者问题

描述

在 Warcraft III 之冰封王座中，毁灭者是不死族打三本后期时的一个魔法飞行单位。

毁灭者的核心技能之一，叫做魔法吸收（Absorb Mana）：

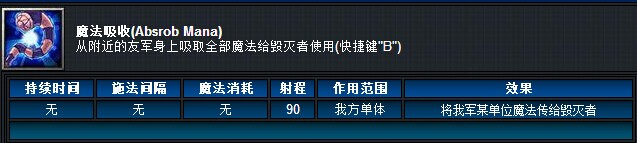
现在让我们来考虑下面的问题：

假设你拥有 n 个魔法单位，他们从左到有站在一行，编号从 1 到 n。 每个单位拥有三项属性：

• si: 初始法力。

• mi: 最大法力上限。

• ri: 每秒中法力回复速度。

现在你操纵一个毁灭者，有 m 个操作，t l r，表示时刻 t，毁灭者对所有编号从 l 到 r 的单位，使用了魔法吸收。操作按照时间顺序给出，计算毁灭者一共吸收了多少法力。

输入

输入数据的第一行有一个整数 n(1 ≤  n ≤105) — 你的魔法单位的数目。

接下来的 n 行，每行有三个整数 si, mi, ri(0 ≤ si ≤ mi ≤ 105, 0 ≤ ri ≤ 105) 描述一个魔法单位。

接下来一行又一个整数 m(1 ≤ m ≤ 105)， — 操作的数目。

接下来的 m 行，每行描述一个操作 t, l, r(0 ≤ t ≤ 109, 1 ≤ l ≤ r ≤ n)，t 非降。

输出

输出一行一个整数表示毁灭者一共吸收了多少法力。

样例输入

5
0 10 1
0 12 1
0 20 1
0 12 1
0 10 1
2
5 1 5
19 1 5

样例输出

83

标准姿势是将操作离线，然后对于每一个位置分别计算，然后用平衡树来维护一些奇怪的东西：

现在不按照时间点进行考虑，而是考虑每个魔法单位都在哪些时间点被抽取了，这样每个魔法单位都有一组被抽取的时间间隔，同时，每个魔法单位都有最大上限M和恢复速度R，考虑某一个魔法单位A的一组时间间隔，按大小分类：

1. 大于等于 (M+R-1)/R 的：意味着抽取的法力为魔法上限M，若满足条件的有K个时间间隔，则该部分抽取的魔法值总和为K*M。
2. 小于(M+R-1)/R的：求和之后乘以R就是该部分抽取的总法力值。
3. 这两部分抽取的总法力值再求和就是A魔法单位被抽取的总法力值。
4. 所有的魔法单位都如此考虑，再求和。

这里关键在于如何维护这些时间间隔，首先需要维护每个魔法单位都有哪些时间点被抽取了，根据这些时间点再来维护时间间隔。

时间点维护：使用一颗伸展树A，对魔法单位1-N 中的每一个i，把以i为开始区间的操作时间点插入到伸展树A中，A在维护过程中保证时间点的序，其实就是一个二叉排序树，插入完成之后，A就维护对魔法单位i进行抽取操作的所有时间点。 
如果在插入一个时间点b的同时，取出该点中序遍历的前驱a和后继c，就意味着，对于i及以后的魔法单位的时间间隔来说，减少了一个:c-a，增加了两个：b-a和c-b。 
并且在魔法单位i的抽取结算之后，从A中删除所有以i为结束区间的操作时间点b，同样得到前驱a和后继c，这意味着i以后的魔法单位的时间间隔减少了两个：c-b和b-a，增加了一个：c-a。

时间间隔维护：仍然使用一颗伸展数B，B维护了时间间隔（同样要保序），并维护附加信息，所有的时间间隔总和sums，以及所有的时间间隔数量size。 
对于前面的时间点维护，每次A插入，都会导致一次B删除和两次B插入； 
同样每次A删除，都会导致两次B删除和一次B插入。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <bitset>
#include <string>
#define PQ priority_queue
#define OO 2147483647
#define Max(a, b) ((FASTBUFFER = ((a) - (b)) >> 31), ((b) & FASTBUFFER | (a) & ~FASTBUFFER))
#define Min(a, b) ((FASTBUFFER = ((a) - (b)) >> 31), ((a) & FASTBUFFER | (b) & ~FASTBUFFER))
#define Swap(a, b) (a ^= b, b ^= a, a ^= b)

using namespace std;

const int N = ;

typedef long long ll;

inline int ran() {
    static int x = ;
    x += (x << ) + ;
    return x & ;
}

struct Node;

typedef pair <Node*, Node*> Pair;

Node *null;

struct Node {
    int val, snow, size;
    ll sum;
    Node *left, *right;

    Node (int val, int snow, Node *left, Node *right) :
        val(val), snow(snow), size(snow), left(left), right(right), sum((ll)val * snow) {}

    Node *Update() {
        size = left->size + snow + right->size;
        sum = left->sum + (ll)val * snow + right->sum;
        return this;
    }

    Pair split(int v);
};

Node *Merge(Node *a, Node *b) {
    if (a == null) {
        return b;
    }

    if (b == null) {
        return a;
    }

    if (ran() % (a->size + b->size) < a->size) {
        a->right = Merge(a->right, b);
        return a->Update();
    }

    b->left = Merge(a, b->left);
    return b->Update();
}

Pair Node :: split(int v) {
    if (this == null) {
        return make_pair(null, null);
    }

    if (val >= v) {
        Pair ret = left->split(v);
        left = ret.second;
        return make_pair(ret.first, this->Update());
    }

    Pair ret = right->split(v);
    right = ret.first;
    return make_pair(this->Update(), ret.second);
}

Node *root;

struct monsterNode {
    int s, m, r;
}a[N];

int n, m;
ll ans;
multiset <int> s;
vector <int> listInsert[N], listErase[N];

void insertWithTreap(int v) {
    Pair ret1 = root->split(v), ret2 = ret1.second->split(v + );
    if (ret2.first->size) {
        ret2.first->snow++;
        ret2.first->size++;
        ret2.first->sum += ret2.first->val;
        root = Merge(ret1.first, Merge(ret2.first, ret2.second));
        return;
    }

    root = Merge(ret1.first, Merge(new Node(v, , null, null), ret2.second));
}

void eraseWithTreap(int v) {
    Pair ret1 = root->split(v), ret2 = ret1.second->split(v + );
    if (ret2.first->size > ) {
        ret2.first->snow--;
        ret2.first->size--;
        ret2.first->sum -= ret2.first->val;
        root = Merge(ret1.first, Merge(ret2.first, ret2.second));
        return;
    }

    root = Merge(ret1.first, ret2.second);
}

void insertQuery(int t) {
    multiset <int> :: iterator it1 = s.lower_bound(t), it2 = s.upper_bound(t);
    if (*it1 == t) {
        s.insert(t);
        return;
    }

    if (it1 != s.begin()) {
        it1--;
    } else {
        it1 = s.end();
    }

    if (it1 != s.end() && it2 != s.end()) {
        eraseWithTreap(*it2 - *it1);
    }

    if (it1 != s.end()) {
        insertWithTreap(t - *it1);
    }

    if (it2 != s.end()) {
        insertWithTreap(*it2 - t);
    }

    s.insert(t);
}

void eraseQuery(int t)
{
    s.erase(s.find(t));
    multiset <int> :: iterator it1 = s.lower_bound(t), it2 = s.upper_bound(t);
    if (*it1 == t) {
        return;
    }

    if (it1 != s.begin()) {
        it1--;
    } else {
        it1 = s.end();
    }

    if (it1 != s.end() && it2 != s.end()) {
        insertWithTreap(*it2 - *it1);
    }

    if (it1 != s.end()) {
        eraseWithTreap(t - *it1);
    }

    if (it2 != s.end()) {
        eraseWithTreap(*it2 - t);
    }
}

void askQuery(int start, int m, int r)
{
    if (s.empty())
        return;
    ans += min((ll)(*s.begin()) * r + start, (ll)m);
    if (r == ) {
        return;
    }

    int full = m / r + ((m % r) > );
    Pair ret = root->split(full);
    ans += (ll)m * ret.second->size;
    ans += ret.first->sum * r;
    root = Merge(ret.first, ret.second);
}

int main() {
    freopen("data1.in","r",stdin);
    freopen("data1.out","w",stdout);
    null = new Node(, , null, null);
    root = null;
    scanf("%d", &n);
    for (int i = ; i <= n; i++) {
        scanf("%d %d %d", &a[i].s, &a[i].m, &a[i].r);
    }

    scanf("%d", &m);
    for (int i = ; i <= m; i++) {
        int t, l, r;
        scanf("%d %d %d", &t, &l, &r);
        listInsert[l].push_back(t);
        listErase[r].push_back(t);
    }

    for (int i = ; i <= n; i++) {
        for (int j = ; j < listInsert[i].size(); j++) {
            insertQuery(listInsert[i][j]);
        }

        askQuery(a[i].s, a[i].m, a[i].r);
        for (int j = ; j < listErase[i].size(); j++) {
            eraseQuery(listErase[i][j]);
        }
    }

    cout << ans << endl;
    return ;
}

用了这么多STL，这代码在我本机起码要跑3s，不知道Hiho上怎么能过？

来讲一讲我的在线做法，首先如果你学过线段树分治的话，你应该知道线段树在打区间修改标记时，打完再向下将标记全部删除的操作并不影响时间复杂度，所以我们可以在此做一些文章。

考虑如何得到[l,r]的答案，其中[l,r]是线段树中的节点，即求sigma(Min(t*ri,mi))。

我们发现这时我们可以用t-setv[o]计算出此区间中所有单位已经积攒的时间（是一样的）。

那么我们只需求出t*ri<=mi的所有节点的ri之和与t*ri>mi的所有节点的mi之和。

对于每个节点i，将mi/ri（向下取整）扔到一个你喜欢的能够支持静态查询区间有多少<x的数据结构里判判就行了。

我用的是主席树，时间复杂度是O(qlog^2n)，可惜被1s的时限卡了将近0.5s。

#include<cstdio>
#include<cctype>
#include<queue>
#include<cmath>
#include<cstring>
#include<algorithm>
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define dwn(i,s,t) for(int i=s;i>=t;i--)
#define ren for(int i=first[x];i!=-1;i=next[i])
using namespace std;
inline int read() {
    int x=,f=;char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c=='-') f=-;
    for(;isdigit(c);c=getchar()) x=x*+c-'';
    return x*f;
}
typedef long long ll;
const int INF=;
const int maxn=;
int root[maxn],ls[maxn*],rs[maxn*],ToT;
ll summ[maxn*],sumr[maxn*],S[maxn],M[maxn],R[maxn];
int n,setv[maxn*];
void insert(int& y,int x,int l,int r,int v,int pos) {
    summ[y=++ToT]=summ[x]+M[v];sumr[y]=sumr[x]+R[v];
    if(l==r) return;ls[y]=ls[x];rs[y]=rs[x];
    int mid=l+r>>;
    if(pos<=mid) insert(ls[y],ls[x],l,mid,v,pos);
    else insert(rs[y],rs[x],mid+,r,v,pos);
}
ll ansm,ansr,ans;
void query(int y,int x,int l,int r,int pos) {
    if(l==r) ansm+=summ[y]-summ[x],ansr+=sumr[y]-sumr[x];
    else {
        int mid=l+r>>;
        if(pos<=mid) query(ls[y],ls[x],l,mid,pos);
        else {
            ansm+=summ[ls[y]]-summ[ls[x]];ansr+=sumr[ls[y]]-sumr[ls[x]];
            query(rs[y],rs[x],mid+,r,pos);
        }
    }
}
void pushdown(int o) {
    int lc=o<<,rc=lc|;
    if(setv[o]>=) {
        setv[lc]=setv[rc]=setv[o];
        setv[o]=-;
    }
}
void build(int o,int l,int r) {
    if(l==r) return;setv[o]=-;
    int mid=l+r>>,lc=o<<,rc=lc|;
    build(lc,l,mid);build(rc,mid+,r);
}
int t,ql,qr,done[maxn];
void getans(int o,int l,int r) {
    if(setv[o]>=) {
        if(l==r&&!done[l]) ans+=min((R[l]-R[l-])*t+S[l],M[l]),done[l]=;
        else {
            int k=t-setv[o];
            if(k) {
                ansm=ansr=;
                query(root[r],root[l-],,INF,k-);
                ans+=ansm+(ll)k*(R[r]-R[l-]-ansr);
            }
        }
        setv[o]=-;
    }
    else {
        int mid=l+r>>,lc=o<<,rc=lc|;
        getans(lc,l,mid);getans(rc,mid+,r);
    }
}
void update(int o,int l,int r) {
    if(ql<=l&&r<=qr) getans(o,l,r),setv[o]=t;
    else {
        pushdown(o);int mid=l+r>>,lc=o<<,rc=lc|;
        if(ql<=mid) update(lc,l,mid);
        if(qr>mid) update(rc,mid+,r);
    }
}
int main() {
    n=read();build(,,n);
    rep(i,,n) {
        S[i]=read(),M[i]=read(),R[i]=read();S[i]=min(S[i],M[i]);
        insert(root[i],root[i-],,INF,i,R[i]?M[i]/R[i]:INF);
        R[i]+=R[i-];
    }
    int q=read();
    while(q--) {
        t=read(),ql=read(),qr=read();
        update(,,n);
    }
    printf("%lld\n",ans);
    return ;
}