hiho #1143 : 骨牌覆盖问题·一 （运用快速幂矩阵）

#1143 : 骨牌覆盖问题·一

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

骨牌，一种古老的玩具。今天我们要研究的是骨牌的覆盖问题：
我们有一个2xN的长条形棋盘，然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘，一共有多少种不同的覆盖方法呢？
举个例子，对于长度为1到3的棋盘，我们有下面几种覆盖方式：

提示：骨牌覆盖

提示：如何快速计算结果

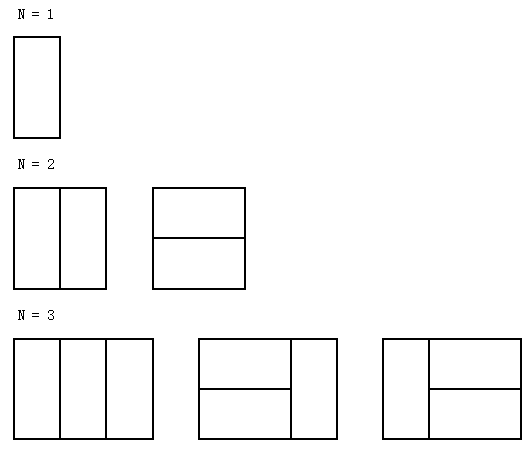
输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 19999997

样例输入

62247088

样例输出

17748018

解题思路：
仔细观察可以看出是Fibonacci函数 f(n)=f(n-1)+f(n-2)。
但当n特别大的时候，运算次数太多，必然超时。
所以引入：

斐波那契数列，快速矩阵幂解法。

当N很小的时候，我们直接通过递推公式便可以计算。当N很大的时候，只要我们的电脑足够好，我们仍然可以直接通过递推公式来计算。
但是我们学算法的，总是这样直接枚举不是显得很Low么，所以我们要用一个好的算法来加速(装X)。
事实上，对于这种线性递推式，我们可以用矩阵乘法来求第n项。对于本题Fibonacci数列，我们希望找到一个2x2的矩阵M，使得(a, b) x M = (b, a+b)，其中(a, b)和(b, a+b)都是1x2的矩阵。
显然，只需要取M = [0, 1; 1, 1]就可以了：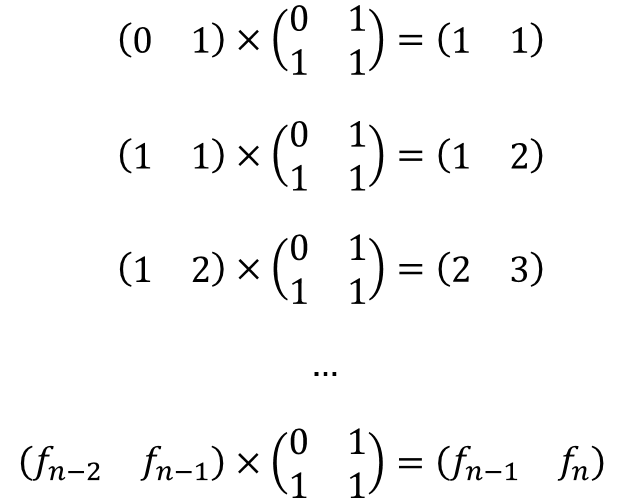

进一步得到：

那么接下来的问题是，能不能快速的计算出M^n？我们先来分析一下幂运算。由于乘法是满足结合律的，所以我们有：

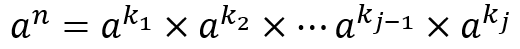
不妨将k[1]..k[j]划分的更好一点？

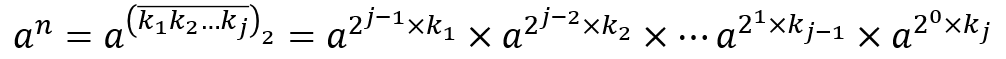
其中(k[1],k[2]...k[j])2表示将n表示成二进制数后每一位的数字。上面这个公式同时满足这样一个性质：

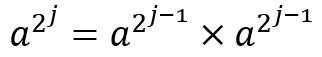
结合这两者我们可以得到一个算法：
1. 先计算出所有的{a^1, a^2, a^4 ... a^(2^j)}，因为该数列满足递推公式，时间复杂度为O(logN)
2. 将指数n二进制化，再利用公式将对应的a^j相乘计算出a^n，时间复杂度仍然为O(logN)
则总的时间复杂度为O(logN)
这种算法因为能够在很短时间内求出幂，我们称之为“快速幂”算法。

AC代码：

 #include"iostream"
 #define MOD 19999997
 using namespace std;

 typedef long long LL;

 struct Matrix
 {
     LL matrix[][];
 }ans,base;

 Matrix mult(Matrix a,Matrix b)
 {
     Matrix c;
     for (int i = ; i < ; i++)
     {
         for (int j = ; j < ; j++)
         {
             c.matrix[i][j] = ;
             for (int k = ; k < ; k++)
             {
                 c.matrix[i][j] += (a.matrix[i][k] * b.matrix[k][j]) % MOD;
             }
             c.matrix[i][j] %= MOD;
         }
     }

     return c;
 }

 LL solve(LL n)
 {
     base.matrix[][] = base.matrix[][] = base.matrix[][] = ;
     base.matrix[][] = ;

     //初始化单位矩阵
     ans.matrix[][] = ans.matrix[][] = ;
     ans.matrix[][] = ans.matrix[][] = ;

     while (n)
     {
         if (n & )
         {
             ans = mult(ans, base);
             //break;
         }
         base = mult(base, base);
         n >>= ;     //n右移一位，n=n>>1  n/2

     }
     return ans.matrix[][] % MOD;

 }

 int main()
 {
     LL n;
     scanf("%lld", &n);

     printf("%lld", solve(n+) % MOD);
     system("pause");
 }