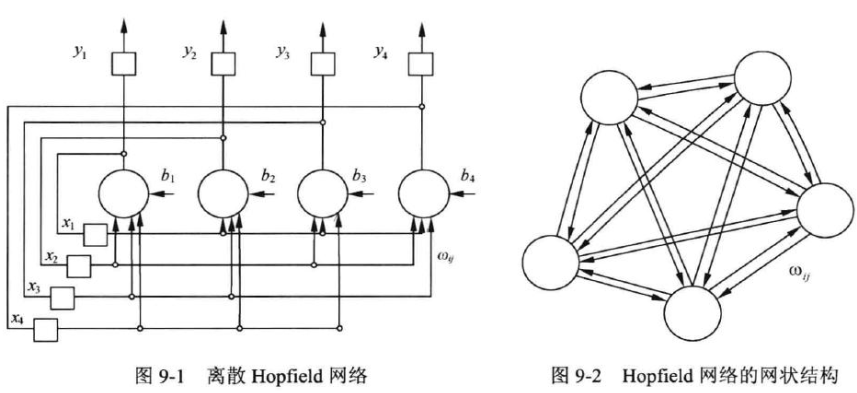
Hopfield 神经网络及稳态性的证明

根据其提出者，John Joseph Hopfield 命名。Hopfield 在 1982 年提出的划时代的：Neural networks and physical systems with emergent collective computational abilities 一文。顾名思义，从论文的名字中我们就可看出，Hopfield 神经网络是将物理学的相关思想（动力学）引入到神经网络的构造当中，事实上，Hopfield 本人正是一位物理学家。

这里所谓动力学的方式，不像 BP 神经网络那样给定输入和输出，通过权值的计算更新以及激活函数的转移，最后能够最小化和输出之间的误差，而动力学的方式则是给模型一定的输入之后，系统就会陷入一个动力学过程里面，反复震荡和计算，最后达到一个稳态。最后能够达到像人一样的具备联想能力的网络。

0. 基本认识

• 每一个神经元和其他神经元都是连接的，因此和 BP 神经网络的不同也在于，Hopfield 神经网络其实没有分层的概念；

1. DHNN

• DHNN，Discrete Hopfield Neural Networks，存在离散型 HNN，自然也少不了 CHNN，Continuous HNN，连续型网络。

• 从其对应的网状结构可以清晰地看出，DHNN 和其他神经网络不同的是，DHNN 并没有层（Layer）的概念，也没有前向和后向的区别。

• bi，称为每一个神经元（neuron）的门槛值，因为最终是要用加权值和减去该值，又可称其为截断值，

  netj=∑i=1nwijxi−Tj,j=1,2,…,n

• 对于输出而言还存在一个反馈回路，第一个神经元的输出会反馈给其他所有神经元，反馈回自己的权值为 0，其他神经元得到的反馈值会作为下一轮的输入值；
  
  wii=0，此外还存在一个对称性的规定，wij=wji

2. 两个定理（稳态性的证明）

吸引子（attractor）：X=f(WX−T)，X 既是输入也是输出，即表明达到稳态；

• 定理之一：对于 DHNN 网，若按异步方式调整网络状态，且连接矩阵 W 为对称阵，则对于任意初态，网络都最终收敛到一个吸引子；

  此时我们引入能量函数（energy function）的定义，

  E(t)=−12XT(t)WX(t)+XT(t)T

  令能量函数的改变量为 ΔE，网络状态的改变量为 ΔX，则有：

  ΔE(t)=E(t+1)−E(t)ΔX(t)=X(t+1)−X(t)

  将相关变量的定义代入进 ΔE(t)，可得：

  ΔE(t)=−12[X(t)+ΔX(t)]TW[X(t)+ΔX(t)]+(X(t)+ΔX(t))TT−E(t)=−ΔXT[WX−T]−12ΔXTWΔX

  由于该定理是规定按照异步工作方式，第 t 个时刻只有一个神经元调整状态，