二维矩阵相乘 in C++

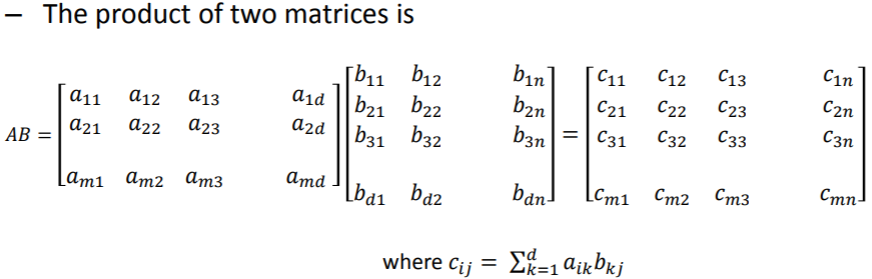
#include <iostream>
#include <vector>
#include <string>
#include <sstream>
#include <fstream>
#include <algorithm>
#include <functional>
#include <numeric>
template <class DataType>
void ReadMatFromFile(std::string &filename, std::vector<std::vector<DataType> > &lines_feat) {
    std::ifstream vm_info(filename.c_str());
    std::string lines;
    DataType var;
    std::vector<DataType> row;
    lines_feat.clear();
    while(!vm_info.eof()) {
        getline(vm_info, lines);
        if(lines.empty())
            break;
        std::stringstream stringin(lines);
        row.clear();
        while(stringin >> var) {
            row.push_back(var);
        }
    lines_feat.push_back(row);
    }
}
template <class T1, class T2>
int MatMultiply(const std::vector<std::vector<T1> > &Mata, const std::vector<std::vector<T2> > &Matb, std::vector<std::vector<T1> > &MatOut) {
    if(Mata.at().size() != Matb.size()) {
        std::cout<<"not match!\n";
        return -;
    }
    for(size_t i=; i<Mata.size(); ++i) {
        for(size_t j=; j<Matb.at().size(); ++j) {
            std::vector<T2> col;
            col.clear();
                for(size_t k=; k<Matb.size(); ++k) {
                    col.push_back(Matb.at(k).at(j));
                }
            MatOut.at(i).at(j)=inner_product(Mata.at(i).begin(), Mata.at(i).end(), col.begin(), );
        }
    }
    return ;
}
template <class T>
void Display2DVector(std::vector<std::vector<T> > &vv) {
    for(size_t i=;i<vv.size();++i) {
        for(typename::std::vector<T>::const_iterator it=vv.at(i).begin();it!=vv.at(i).end();++it) {
            std::cout<<*it<<" ";
        }
        std::cout<<"\n";
    }
    std::cout<<"--------the total of the 2DVector is "<<vv.size()<<std::endl;
}
int main() {
    std::string matfa="mata.dat", matfb="matb.dat";
    std::vector<std::vector<int> > mata, matb;
    ReadMatFromFile(matfa, mata);
    Display2DVector(mata);
    ReadMatFromFile(matfb, matb);
    Display2DVector(matb);
    std::cout<<mata.size()<<"\t"<<matb.at().size()<<std::endl;
    std::vector<std::vector<int> > matout(mata.size(), std::vector<int>(matb.at().size()));
    MatMultiply(mata, matb, matout);
    Display2DVector(matout);
    return ;
}