参考：http://www.cnblogs.com/pinard/p/6251584.html

酉矩阵，关于矩阵的问题，还是很复杂的。

只有方阵才可以进行特征值分解，

但是如果行不等于列，即不是方阵，还能进行特征值分解吗？

答案是可以的，此时我们的svd登场了。【是不是用奇异值代替了特征值】

奇异值有没有特征值的特性呢？？？这是一个问题 。

深入理论才行呀。

下面是SVD进行分解的：（它的两边不是对称的）

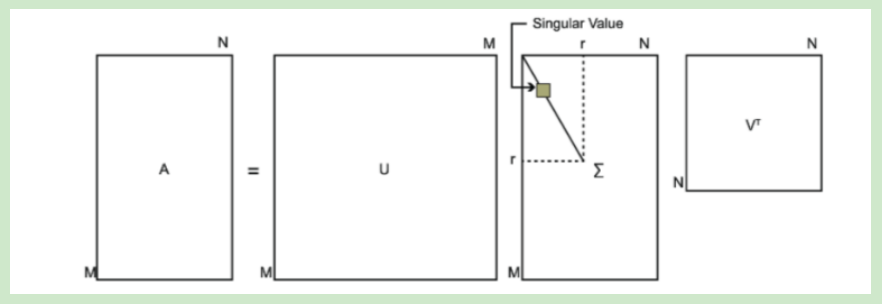
数学就是这样，一些结论记住就好了。（推导太难）

svd 奇异值分解的更多相关文章

  1. SVD奇异值分解的基本原理和运用

    SVD奇异值分解: SVD是一种可靠的正交矩阵分解法.可以把A矩阵分解成U,∑,VT三个矩阵相乘的形式.(Svd(A)=[U*∑*VT],A不必是方阵,U,VT必定是正交阵,S是对角阵<以奇异值 ...

  2. SVD奇异值分解的几何物理意义资料汇总

    学习SVD奇异值分解的网上资料汇总: 1. 关于svd的一篇概念文,这篇文章也是后续几篇文章的鼻祖~ http://www.ams.org/samplings/feature-column/fcarc ...

  3. [机器学习]-SVD奇异值分解的基本原理和运用

    SVD奇异值分解: SVD是一种可靠的正交矩阵分解法.可以把A矩阵分解成U,∑,VT三个矩阵相乘的形式.(Svd(A)=[U*∑*VT],A不必是方阵,U,VT必定是正交阵,S是对角阵<以奇异值 ...

  4. 『科学计算_理论』SVD奇异值分解

    转载请声明出处 SVD奇异值分解概述 SVD不仅是一个数学问题,在工程应用中的很多地方都有它的身影,比如前面讲的PCA,掌握了SVD原理后再去看PCA那是相当简单的,在推荐系统方面,SVD更是名声大噪 ...

  5. 简单易学的机器学习算法—SVD奇异值分解

    简单易学的机器学习算法-SVD奇异值分解 一.SVD奇异值分解的定义     假设M是一个的矩阵,如果存在一个分解: 其中的酉矩阵,的半正定对角矩阵,的共轭转置矩阵,且为的酉矩阵.这样的分解称为M的奇 ...

  6. 对SVD奇异值分解的理解

      首先推荐一篇博客,奇异值分解(SVD)原理详解及推导 - CSDN博客,讲解的很清楚.这里我谈谈自己的理解,方便以后回顾.   如果把向量理解为空间中的一个元素,那么矩阵可以理解为两个空间上的映射 ...

  7. Deep Learning基础--SVD奇异值分解

    矩阵奇异值的物理意义是什么?如何更好地理解奇异值分解?下面我们用图片的例子来扼要分析. 矩阵的奇异值是一个数学意义上的概念,一般是由奇异值分解(Singular Value Decomposition ...

  8. 机器学习（十七）— SVD奇异值分解

    奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域.是 ...

  9. 机器学习降维--SVD奇异值分解

    奇异值分解是有着很明显的物理意义,将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性,让机器学会抽取重要的特征,SVD是一个重要的方法. 所以SVD不仅是一个 ...

  10. SVD奇异值分解

    奇异值分解 备忘:Eigen类库可能会和其他库产生冲突,将Eigen类库的头文件引用放到前面解决了.

随机推荐

  1. PowerDesigner删除外键关系,而不删除外键列[转] 及编码格式

    PowerDesigner删除外键关系,而不删除外键列[转]  数据库 database  -> generate database ->format 设置为utf-8 PowerDesi ...

  2. 第一次接触正则表达式/^[A-Za-z_][A-Za-z0-9_]{5,15}$/

    /^[A-Za-z_][A-Za-z0-9_]{5,15}$/ /^$/ :完整表达式 ^ :表示以什么开始,或者取反 $ :结束 ^[A-Za-z_] : 以字母开始,无论大小都可以: [^A-Za ...

  3. <QT障碍之路>qt中使用串口类接收数据不完整

    问题:当用QT中的serial->readAll()的时候,不会把全部的数据一次性都读取出来,而是阶段性的.原因是因为当串口有信号时候,readyRead()信号就会被抛出,那么一帧完整的数据帧 ...

  4. 学习参考《TensorFlow深度学习》高清中文版PDF+英文版PDF+源代码

    我们知道,TensorFlow是比较流行的深度学习框架,除了看手册文档外,推荐大家看看<Tensorflow深度学习>,共分5方面内容:基础知识.关键模块.算法模型.内核揭秘.生态发展.前 ...

  5. ios-字符串替换-正则表达式-例子

    需求:在html中查找并替换相应的html标签 代码实现 - (NSString *)replaceImageHtml:(NSString *)oldHtml { NSString *regex = ...

  6. [Python] Read and Parse Files in Python

    This lesson will teach you how to read the contents of an external file from Python. You will also l ...

  7. hdu5305 Friends(dfs+map/hash)

    题目:pid=5305">http://acm.hdu.edu.cn/showproblem.php?pid=5305 题意:给定N个人和M条朋友关系,是朋友关系的两个人之间有两种联系 ...

  8. C++模板类代码只能写在头文件？

      这个问题,实际上我几年前就遇到了.最近写个模板类玩的时候,再次遇到.   当我非常仔细的将定义和实现分开,在头文件中保留了最少的依赖后,一切就绪.cpp单独编过.但是当使用的时候,就会报告所有的函 ...

  9. jquery18 css() : 样式的操作

    <!DOCTYPE HTML> <html> <head> <meta http-equiv="Content-Type" content ...

  10. Android全局退出的两种方法

    第一种方法参考<第一行代码>78页 建立一个ActivityCollector类,提供静态方法addActivity,fininshAll(以list为容器) 然后我们建立的Activit ...