BZOJ 1179 抢掠计划atm (缩点+有向无环图DP)

手动博客搬家: 本文发表于20170716 10:58:18, 原地址https://blog.csdn.net/suncongbo/article/details/81061601

https://www.lydsy.com/JudgeOnline/problem.php?id=1179

题意：给定一张有向图，点有点权。给定起点(仅一个)\(s\)与终点集合(多个)\(T\)，问开始于起点、结束于终点集合中的一个点的路径中点权和的最大值。

题解：这里，第一步当然是tarjan缩点。

由于是开始于特定点，dp有些麻烦，建议采用spfa. 但是DP也能做，而且bfs和dfs都能做。只不过，有一些需要注意的地方，很容易写错。

bfs状态转移方程很简单：\(dp[i]\)表示从s出发到i这个点路径点权和的最大值，\(dp[i]=max_{j\in ind[i]}{dp[j]+a[i]}\), a[i]为点权。对于终点集合，我们可以建一个超级终点，每一个终点向超级终点连边，当然也可以朴素地枚举每个终点。但是，有一个细节问题坑了我很久：如果是这样写的：

Tarjan原图中的每一个点;
建新图;
bfs(); (队列中初始只有一个元素s)
ans = dp[超级终点];

则必然会WA. 后来我又对着标程查了好久，问了几位大佬，最后实在没办法对拍了一下，发现生成了这样一组数据成功卡掉自己，经简化如下——

3 2
1 2
3 2
5
1
3
1 1
2
Read 0,Expected 6.

正确的写法应该是：

Tarjan(s); //从s能到达的点
建新图;
bfs(); (队列中初始只有一个元素s)
ans = dp[超级终点];

只有第一行tarjan不一样。为什么呢？

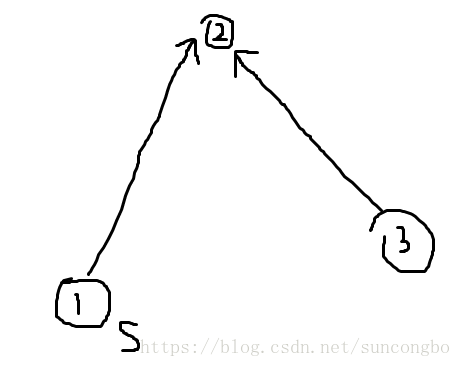
原因是：对于一个点i, 刚才我们讨论的数食物链、字母最多出现次数、最长路径，都是要求\(i\)的所有入边的起点都被更新后才可转移\(i\)(将其加入队列)，bfs的时候从所有入度为0的点开始。但是，现在情况变了，如果我们只从s开始bfs，有一些s走不到的点将永远不会被更新，这样这个点所连向的边也不会被更新，就相当于这个点作废了。但是实际上这个点并未作废。如图所示，如果1号点为起点，2号点为终点，那3号点显然不会被访问到，但是由于2号点有1->2, 3->2两条入边，因此3号点不更新，2号点永远也不会被更新，答案一直是0.但是实际上，2还应该被1更新，因为起点1一定可以通过1->2进入2号点。

实际上，我们确保这种入边的起点先统计的顺序，原因是防止一个点有许多条转移的途径，但是只枚举了其中的一部分，最优解藏在另一部分中的这种情况。但是在这里，所谓“另一部分”是s点永远不可能达到的，因此答案为0，不可能成为最优解，反而还会拖累2号点的更新。



AC代码：

#include<cstdio>
#include<algorithm>
using namespace std;

const int N = 500000;
struct Edge
{
    int v,nxt; bool us;
} e[N+2],e0[N+2];
int fe[N+2],fe0[N+2];
int a[N+2],a0[N+2];
bool f[N+2];
int dfn[N+2],low[N+2];
int sta[N+2];
bool ins[N+2];
int clr[N+2];
int dp[N+2];
int que[N+2];
int ind[N+2];
bool f0[N+2];
int n,m,m0,s,p,tp,cnt,num;

void addedge(int u,int v)
{
    m++; e[m].v = v;
    e[m].nxt = fe[u]; fe[u] = m;
}

void addedge0(int u,int v)
{
    m0++; e0[m0].v = v; ind[v]++;
    e0[m0].nxt = fe0[u]; fe0[u] = m0;
}

void Tarjan(int u)
{
    cnt++; dfn[u] = low[u] = cnt; ins[u] = true;
    tp++; sta[tp] = u;
    for(int i=fe[u]; i; i=e[i].nxt)
    {
        if(dfn[e[i].v]==0) {Tarjan(e[i].v); low[u] = min(low[u],low[e[i].v]);}
        else if(ins[e[i].v]==true) {low[u] = min(low[u],dfn[e[i].v]);}
    }
    if(low[u]==dfn[u])
    {
        num++; clr[u] = num; a0[num] = a[u]; f0[num] = f[u];
        while(sta[tp]!=u)
        {
            ins[sta[tp]] = false;
            clr[sta[tp]] = num;
            a0[num] += a[sta[tp]];
            f0[num] = f[sta[tp]]||f0[num];
            tp--;
        }
        ins[u] = false; tp--;
    }
}

void bfs()
{
    int head = 1,tail = 1; que[tail] = clr[s]; dp[clr[s]] = a0[clr[s]];
    while(head<=tail)
    {
        int cur = que[head]; head++;
        for(int i=fe0[cur]; i; i=e0[i].nxt)
        {
            if(e0[i].us==false)
            {
                ind[e0[i].v]--; e0[i].us = true; dp[e0[i].v] = max(dp[e0[i].v],dp[cur]+a0[e0[i].v]);
                if(ind[e0[i].v]==0)
                {
                    tail++; que[tail] = e0[i].v;
                }
            }
        }
    }
}

int main()
{
    int mm; m = 0; scanf("%d%d",&n,&mm);
    for(int i=1; i<=mm; i++)
    {
        int x,y; scanf("%d%d",&x,&y); addedge(x,y);
    }
    for(int i=1; i<=n; i++) scanf("%d",&a[i]);
    scanf("%d%d",&s,&p);
    for(int i=1; i<=p; i++) {int x; scanf("%d",&x); f[x] = true;}
    cnt = 0; Tarjan(s);
    //for(int i=1; i<=n; i++) if(!dfn[i]) Tarjan(i);
    num++;
    for(int i=1; i<=n; i++)
    {
        for(int j=fe[i]; j; j=e[j].nxt)
        {
            if(clr[i]!=0 && clr[e[j].v]!=0 && clr[i]!=clr[e[j].v])
            {
                addedge0(clr[i],clr[e[j].v]);
            }
        }
    }
    for(int i=1; i<=num; i++) {if(f0[i]==true) addedge0(i,num);}
    bfs();
    printf("%d\n",dp[num]);
    return 0;
}

dfs当然也能做，此处不再赘述。