算法87-----DAG有向无环图的拓扑排序

一、题目：课程排表---210

课程表上有一些课，是必须有修学分的先后顺序的，必须要求在上完某些课的情况下才能上下一门。问是否有方案修完所有的课程？如果有的话请返回其中一个符合要求的路径，否则返回[].

例子1：

Input: 2, [[1,0]]
Output: [0,1]
Explanation: There are a total of 2 courses to take. To take course 1 you should have finished  
             course 0. So the correct course order is [0,1].

例子2：

Input: 4, [[1,0],[2,0],[3,1],[3,2]]
Output: [0,1,2,3] or [0,2,1,3]

Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both    
             courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
             So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3] .

BFS思路：每次找入度为0的节点。

1、先建立图（邻接表）、和入度表。

2、循环n次（n为节点数），每次找到度为0 的节点（循环n次，从头开始找），加入path中，然后将其出度的节点的入度-=1（循环入度表）。

先是找到入度为0的节点：1 将1加入path中，然后是2，3节点的入度减去1，因为1已经被处理掉了。 此时度为0的节点是2，3。 将2，3加入path中，……

伪代码：

循环n次:

循环n次：

找入度为0的节点

将度为0节点加入path中

循环入度表：

将度为0节点的出度节点的入度节点-=1

代码：

from collections import defaultdict
def BFS(n,arr):
    # n 为节点数，arr为【【u1,v1】，【u2,v2】……】，这里的u和v中，v是u的父节点。
    if not arr:
        return -1
    graph = defaultdict(list)
    indegree = defaultdict(int)
    path = []
    for u , v in arr:
        graph[v].append(u)
        indegree[u] += 1
    for i in range(n):
        zeroDegree = False
        for j in range(n):
            if indegree[j] == 0:
                zeroDegree = True
                break
        if not zeroDegree:
            return []
        indegree[j] -= 1
        path.append(j)
        for val in graph[j]:
            indegree[val] -= 1
    return path
n= 5
arr = [[1,0],[2,0],[3,1],[3,2],[4,0]]
print(BFS(n,arr))

DFS思路：递归

　　1、建立图

　　2、循环n次，每次是遍历一个节点是否已经visited且合法地加入path中了，如果False不合法则直接返回【】。

　　3、遍历一个节点时会将其后面的所有子节点都处理掉。

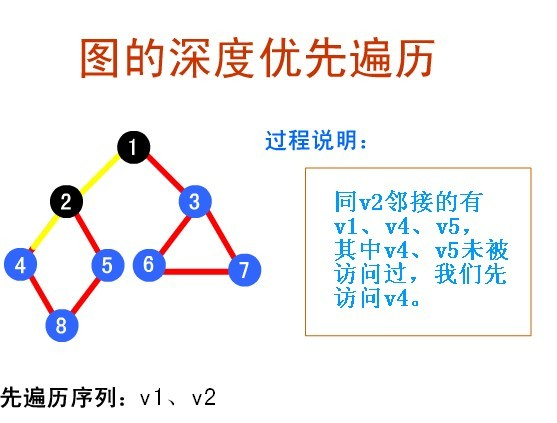
如，先是1，将1进行dfs处理【path中加入1，2，4，8，5】 　　然后是2，将2进行dfs处理，已经visited过了，继续循环 　　然后是3，将3进行dfs处理，没有visited，unkown状态，【path=【1，2，4，8，5】中加入【3，6，7】】 　　然后是4……，后面都是visited过的，都直接跳过。

　

代码：

from collections import defaultdict
def findPath(n,arr):
    if n == 0:
        return []
    graph = defaultdict(list)
    for u , v in arr:
        graph[v].append(u)
    # 0为Unkown，1为visiting，2为visited
    path = []
    visited = [0] * n
    for i in range(n):
        if not DFS(graph,visited,path,i):
            return []
    return path
def DFS(graph,visited,path,i):
    ####i节点：其正在遍历，但它的子节点的子节点也是它，表示产生了有环，则return FALSE
    if visited[i] == 1: return False
    ####i节点 ：已经遍历过，后面已经没有节点了，return true
    elif visited[i] == 2:return True
    ####表示正在遍历i节点
    visited[i] = 1
    for j in graph[i]:
        if not DFS(graph,visited,path,j):
            return False
    path.append(i)
    visited[i] = 2
    return True

n = 5
arr = [[1,0],[2,0],[3,1],[3,2],[4,0]]
print(findPath(n,arr))

二、题目二：课表安排【判断拓扑排序有无环】

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，判断是否可能完成所有课程的学习？

示例 1:

输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

示例 2:

输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

说明:

1. 输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
2. 你可以假定输入的先决条件中没有重复的边。

提示:

1. 这个问题相当于查找一个循环是否存在于有向图中。如果存在循环，则不存在拓扑排序，因此不可能选取所有课程进行学习。
2. 通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程（21分钟），介绍拓扑排序的基本概念。

3. 拓扑排序也可以通过 BFS 完成。

 代码：

from collections import defaultdict
class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: bool
        """
        if numCourses == 0:
            return False
        if len(prerequisites) == 0 or len(prerequisites) <= 1:
            return True

        graph = defaultdict(list)
        indegree = defaultdict(int)
        for u , v in prerequisites:
            graph[v].append(u)
            indegree[u] += 1
        ###BFS,判断是否是拓扑排序
        def BFS(n,graph,indegree,j):
            zerodegree = False
            for i in range(n):
                if indegree[i] == 0:
                    zerodegree = True
                    break
            if not zerodegree:
                return False
            indegree[i] -= 1
            for k in graph[i]:
                indegree[k] -= 1
            return True
        for j in range(numCourses):
            if not BFS(numCourses,graph,indegree,j):
                return False
        return True