与图论的邂逅04:LCT
本着对数据结构这一块东西的一股兴趣,最近在集训的百忙之中抽空出来学LCT,终于学懂了这个高级玩意儿。
前置知识:Splay和树链剖分
Splay挺复杂的......这里就先不写,不然篇幅太大。树链剖分倒是可以大致地讲一下。
树链剖分
什么是树链剖分呢?就是把树给解剖成一条条的链子啦~那就先从最常用的重链剖分讲起。对于当前节点u和它的儿子构成的点集V,若size[v]=max{size[w] | w∈V},也就是以u的儿子为根的所有子树中size最大的那个儿子是v,那么称v是u的重儿子(定义size[x]:以x为根的子树所含有的点数)。如果这时把u向v连一条边,并且其它所有点也像这么做(连向它们的重儿子,叶子节点除外),由于重儿子唯一,父亲唯一,所以就会形成一条一条的链。这个链就叫重链。重链剖分是如此,类比一下就能够理解长链剖分:每个点连向子树深度最大的那个儿子。然而这两种剖法都不是LCT所使用的。LCT使用的是:实链剖分。
实链剖分就是说,把某个节点向它的某个儿子连实边,向其它儿子连虚边,这样也能连出一条条链子。实链剖分有什么好处呢?重链剖分和长链剖分中的size和dep都是固定的,也就是说剖完一棵树之后就无法再改变。而注意刚才实链剖分定义中的一句话:"把某个节点向它的某个儿子连实边",也就是说这个"某个儿子"是可以改变的。那么实链剖分就应运而生并用于解决更灵活的问题。
如果你觉得还不清楚,你可以看一下苯蒟蒻对重链剖分一点点浅显的理解:https://www.cnblogs.com/akura/p/10692600.html,然后类比地这些链剖分应该就可以理解了。
LCT
LCT使用Splay作为辅助树来维护实链,其Splay平衡的关键字为深度。也就是说,右边的点深度大于根,左边的点深度小于根。下面是LCT的相关操作:
access(x)
指打通x到根节点之间的路径,即建立一条从根节点连向x的实链。只需要从x一个链子一个链子地往上跳,并且把跳到的链子改一下即可。原本x到根节点路径上的点可能属于其它的实链,也就是说它的儿子不在x到根节点的路径上——这时把这对父子关系的边断掉即可:
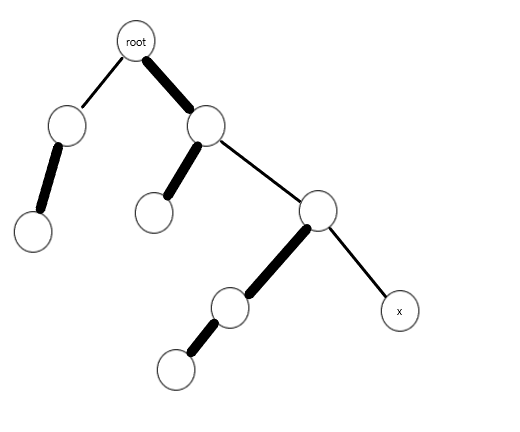
图中粗的是Splay维护的实链,细的是轻边。access之后成了这个样子:
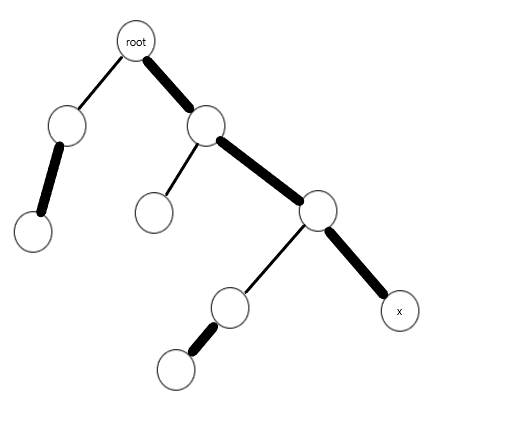
也就是说,我往上连链子的时候碰到一个点,我不管它之前连的哪条链子,都给他断掉,连上我要的链子。
inline void access(int x){ for(int y=;x;ch[x][]=y,update(x),x=fa[y=x]) splay(x); }
每次把x旋到当前Splay的根节点处,往上连边。由于改变了Splay,所以要update一下。
makeroot(x)
指让x成为当前的根。很简单,只需打通x到根节点的路径,然后用splay把x旋到链子顶端即可。最后不要忘了reverse(因为dep发生了改变)。
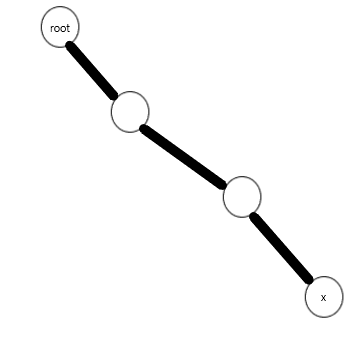
这是access之后x和根节点之间的实链;
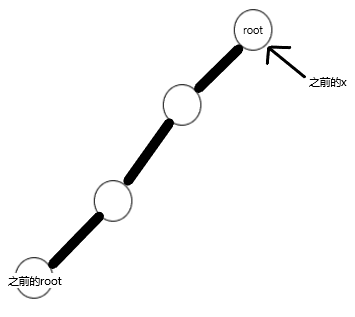
这是splay了并且reverse过的这条链子。
inline void makeroot(int x){ access(x),splay(x),rev(x); }
//rev为reverse
split(x,y)
指打通x到y的路径。先用makeroot(x)让x成为树根,然后用access(y)打通y到根节点(也就是x)的路径即可。最后为了保证复杂度,把y节点splay一下。
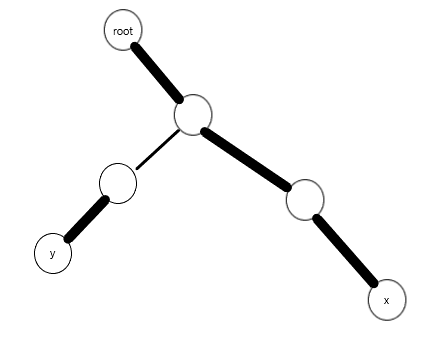
然后makeroot(x)。
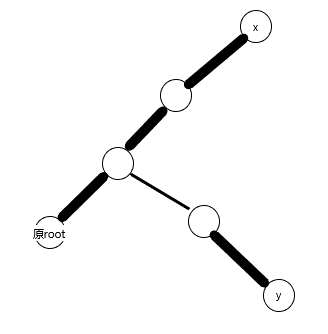
再access。
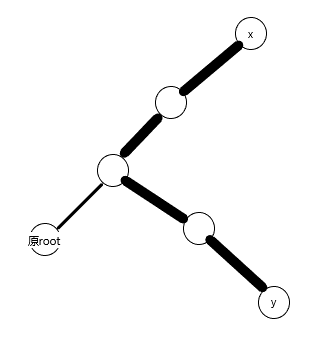
最后splay一下,就不画了。(splay的部分都不画了吧......太麻烦)
inline void split(int x,int y){ makeroot(x),access(y),splay(y); }
findroot(x)
寻找x所在原树的树根。先access(x)打通根到x的路径,然后splay把x旋到Splay的根。此时树的形态发生改变,所以要下传标记。由于根的深度是最小的,所以此时从x开始往Splay的左儿子一直走,最后走到的点就是根。为了保证复杂度,最后再splay一下根。
inline int findroot(int x){ access(x),splay(x),down(x); while(ch[x][]) x=ch[x][],down(x); return splay(x),x; }
link(x,y)
从x往y连一条边。首先makeroot(x)让x成为根,此时link(x,y)是合法的当且仅当findroot(y)!=x即y所在原树的根不是x。这时只需让fa[x]=y即可。不要忘了update(y)更新一下儿子的信息。
inline void link(int x,int y){ makeroot(x); if(findroot(y)!=x) fa[x]=y,update(y); }
cut(x,y)
切断x与y之间的边。首先还是makeroot(x)让x成为根,此时cut(x,y)是合法的当且仅当findroot(y)=x并且fa[y]=x并且ch[y][0]=0。最后一个条件是什么意思呢?由于Splay中左儿子的深度小于根,所以若ch[y][0]不为0,则说明还有比y深度更小的点介于x与y之间,此时不能删边。判断合法之后,修改两个节点的信息,令ch[x][1]=0,fa[y]=0即可。还是不要忘了更新一下x的儿子的信息。
inline void cut(int x,int y){ makeroot(x); if(findroot(y)==x&&fa[y]==x&&!ch[y][]) ch[x][]=fa[y]=,update(x); }
以上就是LCT的最基础的操作(苯蒟蒻还没有学其它的高级操作)。难理解的部分都画了图,应该是能看懂的。
最后对着模板题放个代码:
给定n个点以及每个点的权值,要你处理接下来的m个操作。操作有4种。操作从0到3编号。点从1到n编号。
0:后接两个整数(x,y),代表询问从x到y的路径上的点的权值的xor和。保证x到y是联通的。
1:后接两个整数(x,y),代表连接x到y,若x到y已经联通则无需连接。
2:后接两个整数(x,y),代表删除边(x,y),不保证边(x,y)存在。
3:后接两个整数(x,y),代表将点x上的权值变成y。
#include<iostream>
#include<cstring>
#include<cstdio>
#define maxn 300001
using namespace std;
typedef long long ll; inline int read(){
register int x(),f(); register char c(getchar());
while(c<''||''<c){ if(c=='-') f=-; c=getchar(); }
while(''<=c&&c<='') x=(x<<)+(x<<)+(c^),c=getchar();
return x*f;
}
inline void swap(ll &a,ll &b){ register int tmp; tmp=a,a=b,b=tmp; } int ch[maxn][],fa[maxn],lz[maxn];
ll sum[maxn],val[maxn]; inline int isroot(int x){ return ch[fa[x]][]==x||ch[fa[x]][]==x; }
inline int getson(int x){ return ch[fa[x]][]==x; }
inline void update(int x){ sum[x]=val[x]^sum[ch[x][]]^sum[ch[x][]]; }
inline void rev(int x){ lz[x]^=; swap(ch[x][],ch[x][]); }
inline void down(int x){ if(lz[x]){ if(ch[x][]) rev(ch[x][]); if(ch[x][]) rev(ch[x][]); } lz[x]=; }
inline void rotate(int x){
int y=fa[x],z=fa[y],k=getson(x),w=ch[x][k^];
if(isroot(y)) ch[z][getson(y)]=x;fa[x]=z;
ch[x][k^]=y,fa[y]=x;
if(w) fa[w]=y; ch[y][k]=w;
update(y);
}
inline void splay(int x){
int y,z,stack[maxn]; y=x,z=,stack[++z]=y;
while(isroot(y)) y=fa[y],stack[++z]=y; while(z) down(stack[z--]);
for(y=fa[x]; isroot(x); rotate(x),y=fa[x]) if(isroot(y)) rotate(getson(y)^getson(x)?x:y); update(x);
} inline void access(int x){ for(int y=;x;ch[x][]=y,update(x),x=fa[y=x]) splay(x); }
inline void makeroot(int x){ access(x),splay(x),rev(x); }
inline void split(int x,int y){ makeroot(x),access(y),splay(y); }
inline int findroot(int x){ access(x),splay(x),down(x); while(ch[x][]) x=ch[x][],down(x); return splay(x),x; }
inline void link(int x,int y){ makeroot(x); if(findroot(y)!=x) fa[x]=y,update(y); }
inline void cut(int x,int y){ makeroot(x); if(findroot(y)==x&&fa[y]==x&&!ch[y][]) ch[x][]=fa[y]=,update(x); } int main(){
int n=read(),m=read();
for(register int i=;i<=n;i++) sum[i]=val[i]=read();
for(register int i=;i<=m;i++){
int op=read(),x=read(),y=read();
if(op==) split(x,y),printf("%lld\n",sum[y]);
if(op==) link(x,y);
if(op==) cut(x,y);
if(op==) splay(x),val[x]=y;
}
return ;
}
与图论的邂逅04:LCT的更多相关文章
- 与图论的邂逅03:Lengauer-Tarjan
回想一下,当我们在肝无向图连通性时,我们会遇到一个神奇的点——它叫割点.假设现在有一个无向图,它有一个割点,也就是说把割点删了之后图会分成两个联通块A,B.设点u∈A,v∈B,在原图中他们能够互相到达 ...
- 与图论的邂逅01:树的直径&基环树&单调队列
树的直径 定义:树中最远的两个节点之间的距离被称为树的直径. 怎么求呢?有两种官方的算法(不要问官方指谁我也不晓得): 1.两次搜索.首先任选一个点,从它开始搜索,找到离它最远的节点x.然后从x开始 ...
- 与图论的邂逅07:K短路
在做最短路的题时我们不免会碰到许多求次短路的题,然而我们也能很快地想到解决的办法: 用dijkstra跑一遍最短路,当终点第二次被取出时就是次短路了.时间复杂度为O((N+M)logN).实际上前面得 ...
- 与图论的邂逅06:dfs找环
当我在准备做基环树的题时,经常有了正解的思路确发现不会找环,,,,,,因为我实在太蒻了. 所以我准备梳理一下找环的方法: 有向图 先维护一个栈,把遍历到的节点一个个地入栈.当我们从一个节点x回溯时无非 ...
- 与图论的邂逅05:最近公共祖先LCA
什么是LCA? 祖先链 对于一棵树T,若它的根节点是r,对于任意一个树上的节点x,从r走到x的路径是唯一的(显然),那么这条路径上的点都是并且只有这些点是x的祖先.这些点组成的链(或者说路径)就是x的 ...
- 数据结构&图论:LCT
HDU4010 类比静态区间问题->动态区间问题的拓展 我们这里把区间变成树,树上的写改删查问题,最最最常用LCT解决 LCT用来维护动态的森林,对于森林中的每一棵树,用Splay维护. LCT ...
- thinkjs与Fine Uploader的邂逅
最近在做一个内部系统,需要一个无刷新的上传功能,找了许久,发现了一个好用的上传工具-Fine Uploader,网上也有不少关于它的介绍,对我有不少的启发,结合我的使用场景简单的介绍一下它与t ...
- hdu 5398 动态树LCT
GCD Tree Time Limit: 5000/2500 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Su ...
- 【图论】信手拈来的Prim,Kruskal和Dijkstra
关于三个简单的图论算法 prim,dijkstra和kruskal三个图论的算法,初学者容易将他们搞混,所以放在一起了. prim和kruskal是最小生成树(MST)的算法,dijkstra是单源最 ...
随机推荐
- numpy创建array【老鱼学numpy】
在上一篇文章中,我们已经看到了如何通过numpy创建numpy中的数组,这里再重复一下: import numpy as np # 数组 a = [[1, 2, 3], [4, 5, 6]] prin ...
- 【转】【数据结构】【有n个元素依次进栈,则出栈序列有多少种】
卡特兰数 大神解释:https://blog.csdn.net/akenseren/article/details/82149145 权侵删 原题 有一个容量足够大的栈,n个元素以一定的顺序 ...
- C# ToString()和Convert.ToString()的区别【转】
一.一般用法说明 ToString()是Object的扩展方法,所以都有ToString()方法;而Convert.ToString(param)(其中param参数的数据类型可以是各种基本数据类型, ...
- js 类数组对象arguments
function Add() { for (var i = 0; i < arguments.length; i++) { console.log(arguments[i]); } } Add( ...
- angular.formJson()
<!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title> ...
- 7. Buffer_包描述文件_npm常用指令_fs文件读写_模块化require的规则
1. Buffer 一个和数组类似的对象,不同是 Buffer 是专门用来保存二进制数据的. 特点: 大小固定: 在创建时就确定了,且无法调整 性能较好: 直接对计算机的内存进行操作 每个元素大小为1 ...
- tp5 查询单个字段的值
$num_lastday = Db::name('test_wx') ->where('num','=',$data['num']) ->order('time desc') ->l ...
- scrapy入门使用
scrapy入门 创建一个scrapy项目 scrapy startporject mySpider 生产一个爬虫 scrapy genspider itcast "itcast.cn&qu ...
- 为ivew的Page组件的跳页增加跳页确定按钮
首次使用vue做后台管理项目,首次使用ivew框架,好不容易所有的功能都做完了,前几天产品经理让在每个列表的跳页后面加个‘确定’按钮,说没有确定按钮有点反人类,心想那还不分分钟的事儿嘛,立马回个‘好的 ...
- px,em,rem的区别与用法
别人总结的.个人觉得特别的好: http://www.w3cplus.com/css/when-to-use-em-vs-rem.html
