python 实现进制转换（二进制转十进制）

摘自https://baike.baidu.com/item/%E5%8D%81%E8%BF%9B%E5%88%B6%E8%BD%AC%E4%BA%8C%E8%BF%9B%E5%88%B6

python实现进制转换：https://www.cnblogs.com/cookie1026/p/6059766.html

十进制转二进制

编辑

1. 十进制整数转换为二进制整数

十进制整数转换为二进制整数采用"除2取余，逆序排列"法。

具体做法是：用2整除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为小于1时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。

十进制整数转二进制

如：255=（11111111）

如：=（）B
/======余1
/=======余1
/========余1
/========余1
/=========余1
/==========余1
/==========余1
/==========余1
=(B)
/= 余1 第10位
/= 余0 第9位
/= 余1 第8位
/= 余0 第7位
/= 余1 第6位
/= 余0 第5位
/= 余0 第4位
/= 余0 第3位
/= 余1 第2位
/= 余1 第1位
原理：
众所周知，二进制的基数为2，我们十进制化二进制时所除的2就是它的基数。谈到它的原理，就不得不说说关于位权的概念。某进制计数制中各位数字符号所表示的数值表示该数字符号值乘以一个与数字符号有关的常数，该常数称为 “位权 ” 。位权的大小是以基数为底，数字符号所处的位置的序号为指数的整数次幂。十进制数的百位、十位、个位、十分位的权分别是10的2次方、10的1次方、10的0次方，10的-1次方。二进制数就是2的n次幂。
按权展开求和正是非十进制化十进制的方法。
下面我们开讲原理，举个十进制整数转换为二进制整数的例子，假设十进制整数A化得的二进制数为edcba 的形式，那么用上面的方法按权展开， 得
A=a(^)+b(^)+c(^)+d(^)+e(^) （后面的和不正是化十进制的过程吗）
假设该数未转化为二进制,除以基数2得
A/=a(^)/+b(^)/+c(^)/+d(^)/+e(^)/
注意：a除不开二，余下了！其他的绝对能除开，因为他们都包含2，而a乘的是1，他本身绝对不包含因数2，只能余下。
商得：
b(^)+c(^)+d(^)+e(^)，再除以基数2余下了b，以此类推。
当这个数不能再被2除时，先余掉的a位数在原数低，而后来的余数数位高，所以要把所有的余数反过来写。正好是edcba

 

 

 

 

 

 

 

 

 

二进制转十进制

整数部分要从右到左用二进制的每个数去乘以2的相应次方

小数点后则是从左往右

例如：二进制数1101.01转化成十进制

所以总结起来通用公式为：

abcd.efg(2)=d*20+c*21+b*22+a*23+e*2-1+f*2-2+g*2-3（10）

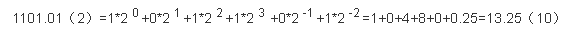
或者用下面这种方法：
把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。这种做法称为"按权相加"法。
2的0次方是1（任何数的0次方都是1，0的0次方无意义）
2的1次方是2
2的2次方是4
2的3次方是8
2的4次方是16
2的5次方是32
2的6次方是64
2的7次方是128
2的8次方是256
2的9次方是512
2的10次方是1024
2的11次方是2048
2的12次方是4096
2的13次方是8192
2的14次方是16384
2的15次方是32768
2的16次方是65536
2的17次方是131072
2的18次方是262144
2的19次方是524288
2的20次方是1048576
即：

此时，=+++=
再比如：二进制数100011转成十进制数可以看作这样：
数字中共有三个1 即第一位一个，第五位一个，第六位一个，然后对应十进制数即2的0次方+2的1次方+2的5次方， 即
=+++++=