浅谈Tarjan算法

从这里开始

• 预备知识
• 两个数组
• Tarjan 算法的应用
  • 求割点和割边
  • 求点-双连通分量
  • 求边-双连通分量
  • 求强连通分量

预备知识

　　设无向图$G_{0} = (V_{0}, E_{0})$，其中$V_{0}$为定点集合，$E_{0}$为边集，设有向图$G_{1} = (V_{1}, E_{1})$，其中$V_{1}$为定点集合，$E_{1}$为边集。

• 无向图中的路径：如果存在一个顶点序列$v_{p},v_{i_{1}},\cdots,v_{i_{k}},v_{q}$，使得$\left ( v_{p}, v_{i_{1}} \right ),\left ( v_{i_{1}},v_{i_{2}} \right ),\cdots,\left ( v_{k-1}, v_{k} \right ),\left ( v_{k}, v_{q} \right )\in E_{0}$，那么称$v_{p}$到$v_{q}$之间存在一条路径。
• 有向图中的路径：如果存在一个顶点序列$v_{p},v_{i_{1}},\cdots,v_{i_{k}},v_{q}$，使得$\left ( v_{p}, v_{i_{1}} \right ),\left ( v_{i_{1}},v_{i_{2}} \right ),\cdots,\left ( v_{k-1}, v_{k} \right ),\left ( v_{k}, v_{q} \right )\in E_{1}$，那么称$v_{p}$到$v_{q}$之间存在一条路径。
• 连通图：在无向图中，对于任意有序对$\left ( v_{i},v_{j} \right )\in(V_{0}\times V_{0})$，都存在一条$v_{i}$到$v_{j}$的路径。
• 强连通图：在有向图中，对于任意有序对$\left ( v_{i},v_{j} \right )\in(V_{1}\times V_{1})$，都存在一条$v_{i}$到$v_{j}$的路径。
• 连通分量：无向图$G$的极大连通子图是$G$的连通分量。
• 强连通分量：有向图$G$的极大强连通子图是$G$的强连通分量。
• 割点：在无向图$G$中，如果存在点$v_{0}$满足删除它后，新图的连通分量的个数增加，那么$v_{0}$为原图的一个割点。
• 割边（又称为桥）：在无向图$G$中，如果存在边$e_{0}$满足删除它后，新图的连通分量的个数增加，那么$e_{0}$为原图的一条割边。
• 边-双连通图：若无向连通图$G$中不存在割边，则无向图$G$是边-双连通图
• 点-双连通图：若无向连通图$G$中不存在割点，则无向图$G$是点-双连通图
• 点-双连通分量：无向图$G$中的极大点-双连通子图是它的点-双连通分量
• 边-双连通分量：无向图$G$中的极大边-双连通子图是它的边-双连通分量

两个数组

　　$dfn_i$：点$i$的深度优先数（英文可能是Depth First Number），可以理解为是第几个被搜索到的节点。

　　$low_i$：在点$i$的dfs子树中通过1条返祖边到达的最早祖先。

　　Tarjan算法首先会对原图进行深度优先搜索。

　　当从一个访问过的点通过边$e$到达一个未访问的点，则将边$e$标记为树边。如果一条非树边$(u, v)$使得要么$u$是$v$的祖先满足，要么$v$是$u$的祖先，那么称边$(u, v)$是一条返祖边。

　　显然当遇到一条返祖边时，需要用它来更新当前点的$low$值

　　通过Tarjan算法得到的生成森林是dfs生成森林：

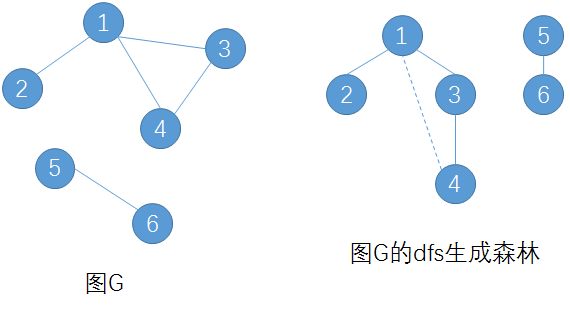
　　（其中虚边是返祖边）

Tarjan算法的应用

求割点和割边

　　首先给出一个结论

定理1 无向图中的每一条边，要么是树边，要么是返祖边。

　　证明 假如存在其他边，它满足它不连它的祖先也不连它的后代，那么它一定是满足：

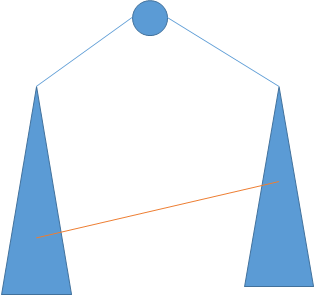
　　然后根据dfs的性质和无向边的性质，容易得到不存在这种情况。

　　假如现在考虑点$p$是不是割点，分两种情况讨论：

• 如果$p$是树根，那么只要$p$的子节点个数大于1，那么$p$就是割点。因为$p$不存在祖先，点$p$的不同子树中的两点之间的路径必须经过点1（因为根节点的位于它不同子树内的两点的LCA是根节点，然后根据定理1得到，从其中一个点开始走，经过的每一条边要么到它的后代要么到它的祖先，所以必定经过1）。
• 如果$p$不是树根，那么只要存在一个子节点$x$满足$low_x \geqslant dfn_p$，那么点$p$是割点。因为假如点$p$被删掉后，点$x$无法到达$p$的祖先，而这之前是可以到达的，所以连通分量的个数至少增加了1.

Code

 /**
  * poj
  * Problem#1144
  * Accepted
  * Time: 16ms
  * Memory: 672k
  */
 #include <algorithm>
 #include <iostream>
 #include <cstring>
 #include <cstdio>
 #include <vector>
 using namespace std;
 typedef bool boolean;

 const int N = ;

 int n;
 int cnt, res;
 int dfn[N], low[N];
 boolean vis[N];
 vector<int> g[N];

 inline boolean init() {
     scanf("%d", &n);
     if (!n)    return false;
     for (int i = ; i <= n; i++)
         g[i].clear();
     int u, v;
     while (~scanf("%d", &u) && u) {
         while (getchar() != '\n') {
             scanf("%d", &v);
             g[u].push_back(v);
             g[v].push_back(u);
         }
     }
     return true;
 }

 void tarjan(int p, int fa) {
     int cson = ;
     dfn[p] = low[p] = ++cnt;
     vis[p] = true;
     for (int i = ; i < (signed)g[p].size(); i++) {
         int e = g[p][i];
         if (e == fa)    continue;
         if (!vis[e]) {
             tarjan(e, p);
             low[p] = min(low[p], low[e]);
             if (low[e] >= dfn[p])
                 cson++;
         } else
             low[p] = min(low[p], dfn[e]);
     }
     if ((!fa && cson > ) || (fa && cson))
         res++;
 }

 inline void solve() {
     cnt = , res = ;
     memset(vis, false, sizeof(boolean) * (n + ));
     for (int i = ; i <= n; i++)
         if (!vis[i])
             tarjan(i, );
     printf("%d\n", res);
 }

 int main() {
     while (init()) {
         solve();
     }
     return ;
 }

Cut Vectex

　　求桥的话，相对就简单一些。

　　一个非常显然的结论：

定理2 返祖边不可能是桥。

　　证明 因为返祖边的两端一定通过树边连通。所以删掉返祖边不会改变图的连通性。

　　因此割边的个数不会超过$n - 1$（一个显然，但没多大用的性质）。

　　我更想说的是，再根据定理1可以得到桥一定是树边。

　　考虑什么样的树边被断掉后图的连通分量的个数增加。假如这条树边两端的点是$u, v$，其中$u$是$v$的爸爸父节点。删掉边$(u, v)$后，连通分量个数增加的充分必要条件是$v$无法通过返祖边到达$u$或者$u$的祖先。因此，不难得到条件是$low_v = dfn_v$。

Code

 /**
  * hdu
  * Problem#4738
  * Accepted
  * Time: 187ms
  * Memory: 25264k
  */
 #include <iostream>
 #include <cstring>
 #include <cstdio>
 using namespace std;
 typedef bool boolean;

 const int N = , M = 2e6 + ;

 typedef class Edge {
     public:
         int end;
         int next;
         int w;

         Edge(int end = , int next = , int w = ):end(end), next(next), w(w) {    }
 }Edge;

 typedef class MapManager {
     public:
         int ce;
         int h[N];
         Edge es[M];

         void addEdge(int u, int v, int w) {
             es[++ce] = Edge(v, h[u], w);
             h[u] = ce;
         }

         void addDoubleEdge(int u, int v, int w) {
             addEdge(u, v, w);
             addEdge(v, u, w);
         }

         Edge& operator [] (int p) {
             return es[p];
         }
 }MapManager;

 int n, m;
 int cnt, res;
 int dfn[N], low[N];
 boolean vis[N];
 MapManager g;

 inline boolean init() {
     scanf("%d%d", &n, &m);
     if (!n && !m)
         return false;
     g.ce = -;
     memset(g.h, -, sizeof(int) * (n + ));
     for (int i = , u, v, w; i <= m; i++) {
         scanf("%d%d%d", &u, &v, &w);
         g.addDoubleEdge(u, v, w);
     }
     return true;
 }

 void tarjan(int p, int laste) {
     dfn[p] = low[p] = ++cnt;
     vis[p] = true;
     for (int i = g.h[p]; ~i; i = g[i].next) {
         int e = g[i].end, w = g[i].w;
         if (i == laste)    continue;
         if (!vis[e]) {
             tarjan(e, i ^ );
             low[p] = min(low[p], low[e]);
             if (low[e] == dfn[e])
                 res = min(res, w);
         } else
             low[p] = min(low[p], dfn[e]);
     }
 }

 inline void solve() {
     cnt = , res = ;
     memset(vis, false, sizeof(boolean) * (n + ));
     tarjan(, -);
     if (!res) res = ;            // 坑....
     for (int i = ; i <= n; i++)
         if (!vis[i]) {
             res = ;
             break;
         }
     if (res == )    res = -;
     printf("%d\n", res);
 }

 int main() {
     while (init())
         solve();
     return ;
 }

Cut Edge

求点-双连通分量

　　在求点-双连通分量（以下简称为点双）之前，我们再来证明一个东西：

定理3 每条边恰好属于一个点双。

　　证明 首先来说明每条边一定属于一个点双连通子图。考虑这条边的两个端点以及它本身构成的子图，显然它是点双连通的。

　　然后来说明任意两个点双没有公共边。

　　假设存在两个点双有一条公共边$(u, v)$，假设它们的点集分别为$V_1, V_2$。如果删掉的点$x\in V_1$或$x\in V_2$，且$x\neq u, x\neq v$，根据点双的定义容易得到新图的连通性不会改变。如果删掉的点是$u$，那么剩余的点一定与$v$连通，所以它仍然不会改变图的连通性。对于如果删掉的点是$v$同理可证不会改变新图的连通性。所以删掉$V_1 \cup V_2$中任意一个点都不会改变图的连通性。因此它们能够组成更大的一个点双连通子图，与点双的定义矛盾。

　　由这个证明过程不难得到点双的点集大小至少为2，所以在考虑找到所有点双的时候可以考虑边。

定理4 每个点双包含至少一条树边。

　　证明 假设存在一个点双不包含任意一条树边。我们考虑从这个点双中选取2个不同点$u, v$，它们在dfs生成树上存在唯一一条路径。我们把它加入这个点双中，如果删掉非路径上的点，那么剩余点与$u, v$连通。如果删掉的是$u$或者$v$，那么剩下点会与另外一个点连通。如果删掉的是路径上的一个点（不含端点），那么路径上一部分点会与$u$连通，另一部分与$v$，$u, v$和原点双中的点一定连通。所以新子图还是一个点双连通子图，与点双的定义矛盾。

　　所以点双的数量不会超过$n - 1$。

　　我们考虑在回溯的时候找到一个点双。

　　考虑判断一条树边是不是一个点双内的树边中深度最低的一条边。假设它深度较深的一端是$v$，较浅的一端是$u$。那么当$v$无法连向$u$的祖先的时候，加入$u$后再加入另一条与$u$连通的树边，那么删掉$u$后就会多产生连通块，所以当$low_v \geqslant dfn_u$的时候，这条边是这个点双内的最后一条边。

　　如果需要求出点双内的所有点和所有边可以用一个栈记录一下边。

　　注意一下返祖边只在子节点的时候加入，这个可以通过判断深度优先数的大小解决掉（你一定也不希望在其他某个点双内莫名其妙多出一条边）。

Code

 /**
  * poj
  * Problem#2942
  * Accepted
  * Time: 1063ms
  * Memory: 1128k
  */
 #include <iostream>
 #include <cstdlib>
 #include <cstdio>
 #include <vector>
 #include <stack>
 using namespace std;
 typedef bool boolean;

 template <typename T>
 void pfill(T* pst, const T* ped, T val) {
     for ( ; pst != ped; *(pst++) = val);
 }

 const int N = 1e3 + , M = (N * N) << ;

 typedef class Edge {
     public:
         int ed, nx;

         Edge(int ed = , int nx = ):ed(ed), nx(nx)    {    }
 }Edge;

 typedef class MapManager {
     public:
         int h[N];
         vector<Edge> es;

         void addEdge(int u, int v) {
             es.push_back(Edge(v, h[u]));
             h[u] = (signed) es.size() - ;
         }

         Edge& operator [] (int p) {
             return es[p];
         }
 }MapManager;

 #define pii pair<int, int>

 int n, m;
 int col[N];
 stack<pii> s;
 MapManager g;
 int dfs_clock;
 boolean res[N];
 MapManager subg;
 boolean rg[N][N];
 int dfn[N], low[N];
 vector<int> bpoints;

 inline boolean init() {
     scanf("%d%d", &n, &m);
     if (!n && !m)
         return false;
     g.es.clear();
     dfs_clock = ;
     pfill(dfn, dfn + n + , );
     pfill(col, col + n + , -);
     pfill(g.h, g.h + n + , -);
     pfill(res, res + n + , false);
     pfill(subg.h, subg.h + n + , -);
     for (int i = ; i <= n; i++)
         for (int j = ; j <= n; j++)
             rg[i][j] = false;
     for (int i = , u, v; i <= m; i++) {
         scanf("%d%d", &u, &v);
         rg[u][v] = rg[v][u] = true;
     }
     return true;
 }

 boolean color(int p, int c) {
     if (~col[p])
         return col[p] == c;
     col[p] = c;
     for (int i = subg.h[p]; ~i; i = subg[i].nx)
         if (!color(subg[i].ed, col[p] ^ ))
             return false;
     return true;
 }

 void dispose() {
     if (!color(bpoints[], )) {
         for (unsigned i = ; i < bpoints.size(); i++)
             res[bpoints[i]] = true;
     }
     for (unsigned i = ; i < bpoints.size(); i++)
         subg.h[bpoints[i]] = -, col[bpoints[i]] = -;
     subg.es.clear();
     bpoints.clear();
 }

 void tarjan(int p, int last_edge) {
     dfn[p] = low[p] = ++dfs_clock;

     pii now, cur;
     for (int i = g.h[p], e; ~i; i = g[i].nx) {
         e = g[i].ed;
         if (i == (last_edge ^ ))
             continue;
         now = pii(min(p, e), max(p, e));
         if (!dfn[e]) {
             s.push(now);
             tarjan(e, i);
             low[p] = min(low[p], low[e]);
             if (low[e] >= dfn[p]) {
                 do {
                     cur = s.top();
                     s.pop();
                     subg.addEdge(cur.first, cur.second);
                     subg.addEdge(cur.second, cur.first);
                     bpoints.push_back(cur.first);
                     bpoints.push_back(cur.second);
                 } while (now != cur);
                 dispose();
             }
         } else {
             low[p] = min(low[p], dfn[e]);
             if (dfn[e] < dfn[p])
                 s.push(pii(min(p, e), max(p, e)));
         }
     }
 }

 inline void solve() {
     for (int i = ; i <= n; i++)
         for (int j = i + ; j <= n; j++)
             if (!rg[i][j]) {
                 g.addEdge(i, j);
                 g.addEdge(j, i);
             }

     for (int i = ; i <= n; i++)
         if (!dfn[i])
             tarjan(i, -);

     int answer = ;
     for (int i = ; i <= n; i++)
         answer += !res[i];
     printf("%d\n", answer);
 }

 int main() {
     while (init())
         solve();
     return ;
 }

Vertex Biconnected Component

　　有时候我们希望求出点双内的点，这个时候栈内记录边略显得麻烦，可以考虑找到一个点的时候加入一个点，它在找到包含它到它的父节点的那条树边的点双时被弹出栈。具体细节可以见代码。

Code

/**
 * loj
 * Problem#2562
 * Accepted
 * Time: 2431ms
 * Memory: 21964k
 */
#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;

const int N = 1e5 + 5, N2 = N << 1;

template <typename T>
void pfill(T* pst, const T* ped, T val) {
	for ( ; pst != ped; *(pst++) = val);
}

typedef class Edge {
	public:
		int ed, nx;

		Edge() {	}
		Edge(int ed, int nx) : ed(ed), nx(nx) {	}
} Edge;

typedef class MapManager {
	public:
		int h[N << 1];
		vector<Edge> es;

		void init(int n) {
			pfill(h + 1, h + n + 1, -1);
			es.clear();
		}

		void add_edge(int u, int v) {
			es.emplace_back(v, h[u]);
			h[u] = (signed) es.size() - 1;
		}
		Edge& operator [] (int p) {
			return es[p];
		}
} MapManager;

int Case;
int n, m;
MapManager G, Tr;

int cnt_node, dfs_clock;
int value[N2];

inline void init() {
	scanf("%d%d", &n, &m);
	G.init(n);
	Tr.init(n << 1);
	cnt_node = n;
	pfill(value + 1, value + n + 1, 1);
	for (int i = 1, u, v; i <= m; i++) {
		scanf("%d%d", &u, &v);
		G.add_edge(u, v);
		G.add_edge(v, u);
	}
}

stack<int> S;
boolean vis[N];
int dfn[N], low[N];

void init_tarjan() {
	dfs_clock = 0;
	while (!S.empty()) S.pop();
	pfill(vis + 1, vis + n + 1, false);
}
void Tarjan(int p) {
	S.push(p);
	vis[p] = true;
	dfn[p] = low[p] = ++dfs_clock;
	for (int i = G.h[p], e; ~i; i = G[i].nx) {
		e = G[i].ed;
		if (!vis[e]) {
			Tarjan(e);
			low[p] = min(low[p], low[e]);
			if (low[e] >= dfn[p]) {
				int now = -1, id = ++cnt_node;
				value[id] = 0;
				do {
					now = S.top();
					S.pop();
					Tr.add_edge(id, now);
					Tr.add_edge(now, id);
				} while (now != e);
				Tr.add_edge(id, p);
				Tr.add_edge(p, id);
			}
		} else {
			low[p] = min(low[p], dfn[e]);
		}
	}
}

int sz[N2], zson[N2], dep[N2];
int in[N2], top[N2], fa[N2];

void dfs1(int p, int Fa) {
	int mx = -1, &id = zson[p];
	sz[p] = 1, fa[p] = Fa;
	value[p] += value[Fa], dep[p] = dep[Fa] + 1, id = -1;
	for (int i = Tr.h[p], e; ~i; i = Tr[i].nx) {
		e = Tr[i].ed;
		if (e ^ Fa) {
			dfs1(e, p);
			sz[p] += sz[e];
			if (sz[e] > mx) {
				mx = sz[e];
				id = e;
			}
		}
	}
}

void dfs2(int p, boolean ontop) {
	in[p] = ++dfs_clock;
	top[p] = (!ontop) ? (top[fa[p]]) : (p);
	if (~zson[p]) {
		dfs2(zson[p], false);
	}
	for (int i = Tr.h[p], e; ~i; i = Tr[i].nx) {
		e = Tr[i].ed;
		if (e != fa[p] && e != zson[p]) {
			dfs2(e, p);
		}
	}
}

int lca(int u, int v) {
	while (top[u] != top[v]) {
		if (dep[top[u]] < dep[top[v]]) {
			swap(u, v);
		}
		u = fa[top[u]];
	}
	return (dep[u] < dep[v]) ? (u) : (v);
}

inline void solve() {
	static int S[N2];

	init_tarjan();
	Tarjan(1);

	dfs_clock = 0;
	dfs1(1, 0);
	dfs2(1, true);

	int Q, K;
	scanf("%d", &Q);
	while (Q--) {
		scanf("%d", &K);
		for (int i = 1; i <= K; i++) {
			scanf("%d", S + i);
		}

		sort(S + 1, S + K + 1, [&] (const int& u, const int& v) {
			return in[u] < in[v];
		});
		int vd = value[fa[lca(S[1], S[K])]];
		int ans = value[S[1]] - vd, g;
		for (int i = 1; i < K; i++) {
			g = lca(S[i], S[i + 1]);
			ans += value[S[i + 1]] - value[g];
		}
		printf("%d\n", ans - K);
	}
}

int main() {
	scanf("%d", &Case);
	while (Case--) {
		init();
		solve();
	}
	return 0;
}

　　然后有一个比较常用的性质：

性质1 点双内任意两个不同点$u, v$之间存在两条公共点只有$u, v$的路径。

　　证明 如果存在两个点$u, v$之间不存在2条公共点只有$u, v$的路径。

　　考虑如果$u, v$之间只存在1条路径，那么删掉这条路径中除去$u, v$外任意一点都会使得图不连通。

　　否则考虑证明存在一个必经点。

　　如果存在2条路径，那么任取一个$u, v$外的一个公共点就是必经点

　　假设存在3条路径，它们两两在$u, v$外

-->

求边-双连通分量

　　（下面将边-双连通分量简写为边双）

　　和点双类似，只不过这次我们考虑顶点：

定理5 每个顶点恰好属于一个边双。

　　证明 首先一个点的图是边双。

　　假设存在两个边双存在一个公共点$x$，那么删掉一条边都不会改变$x$和剩下的点的连通性。

　　我们考虑一个点是不是边双中的最浅的一个点。如果$dfn_p = low_p$，那么再加入它的某个父节点，那么它将成为割点。

　　如果需要求出边双内的所有点再用一个栈记录一下点就好了。

　　似乎还有一种做法是边双内一定不包含原图的桥，因此我们找到所有的桥，把它们删掉就得到了所有边双了。这个条件只是必要性，它的充分性可以考虑如果它删掉后使得连通块个数增加，那么它一定是原图的桥。（它是原图的一个子图，那么再加入若干端点都在它内部边后不会使得它的边连通性降低）。

Code

 /**
  * poj
  * Problem#3177
  * Accepted
  * Time: 47ms
  * Memory: 744k
  */
 #include <iostream>
 #include <cstdlib>
 #include <cstdio>
 #include <vector>
 #include <stack>
 using namespace std;
 typedef bool boolean;

 template <typename T>
 void pfill(T* pst, const T* ped, T val) {
     for ( ; pst != ped; *(pst++) = val);
 }

 const int N = 5e3 + , M = N << ;

 typedef class Edge {
     public:
         int ed, nx;

         Edge(int ed = , int nx = ):ed(ed), nx(nx)    {    }
 }Edge;

 typedef class MapManager {
     public:
         int* h;
         vector<Edge> es;

         MapManager() {    }
         MapManager(int n) {
             h = new int[(n + )];
             pfill(h + , h + n + , -);
         }

         void addEdge(int u, int v) {
             es.push_back(Edge(v, h[u]));
             h[u] = (signed) es.size() - ;
         }

         Edge& operator [] (int p) {
             return es[p];
         }
 }MapManager;

 int n, m;
 int deg[N];
 MapManager g;
 stack<int> s;
 int dfs_clock;
 int dfn[N], low[N];
 pair<int, int> es[M];

 inline void init() {
     scanf("%d%d", &n, &m);
     g = MapManager(n);
     for (int i = , u, v; i <= m; i++) {
         scanf("%d%d", &u, &v);
         g.addEdge(u, v);
         g.addEdge(v, u);
         es[i] = pair<int, int>(u, v);
     }
 }

 void tarjan(int p, int last_edge) {
     dfn[p] = low[p] = ++dfs_clock;
     s.push(p);
     for (int i = g.h[p], e; ~i; i = g[i].nx) {
         e = g[i].ed;
         if (i == (last_edge ^ ))
             continue;
         if (!dfn[e]) {
             tarjan(e, i);
             low[p] = min(low[p], low[e]);
         } else
             low[p] = min(low[p], dfn[e]);
     }

     if (low[p] == dfn[p]) {
         int cur;
         do {
             cur = s.top();
             s.pop();
             low[cur] = low[p];
         } while (cur != p);
     }
 }

 inline void solve() {
     for (int i = ; i <= n; i++)
         if (!dfn[i])
             tarjan(i, -);
     for (int i = ; i <= m; i++) {
         int u = es[i].first, v = es[i].second;
         if (low[u] != low[v])
             deg[low[u]]++, deg[low[v]]++;
     }

     int cnt_leaf = ;
     for (int i = ; i <= n; i++)
         if (dfn[i] == low[i] && deg[low[i]] == )
             cnt_leaf++;
     printf("%d\n", (cnt_leaf + ) >> );
 }

 int main() {
     init();
     solve();
     return ;
 }

Edge Biconnected Component

求强连通分量

　　有向图稍微要麻烦一点，不过基本思想还是一样的。

　　仍然考虑有向图的dfs生成森林，$dfn$数组以及$low$数组。

　　但是有向图中生成森林会复杂许多：

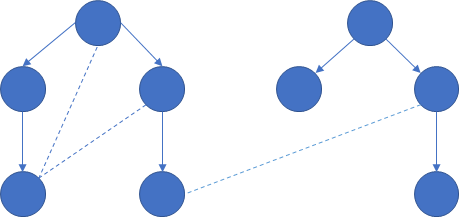
　　在更新$low$的时候要注意两个点是否在同一个子树内。

　　不难注意到一个强连通分量一定是某一个dfs子树内，所以我们仍然考虑一个强连通分量内的最浅点。

　　不难得到它的充分必要条件时$dfn_u = low_u$。必要性是因为，如果它能够到达它的若干级祖先，那么这一条链再加上这一条返祖边就能得到一个强连通子图，充分性显然，因为它自己就能构成一个强连通子图。

　　我们用类似于求边双的方法，就可以求出每个强连通分量内的所有点。 　　

 /**
  * hdu
  * Problem#1269
  * Accepted
  * Time: 46ms
  * Memory: 3944k
  */
 #include <iostream>
 #include <cstdlib>
 #include <cstdio>
 #include <vector>
 #include <stack>
 using namespace std;
 typedef bool boolean;

 template <typename T>
 void pfill(T* pst, const T* ped, T val) {
     for ( ; pst != ped; *(pst++) = val);
 }

 const int N = 1e4 + ;

 typedef class Edge {
     public:
         int ed, nx;

         Edge(int ed = , int nx = ):ed(ed), nx(nx)    {    }
 }Edge;

 typedef class MapManager {
     public:
         int h[N];
         vector<Edge> es;

         void addEdge(int u, int v) {
             es.push_back(Edge(v, h[u]));
             h[u] = (signed) es.size() - ;
         }

         Edge& operator [] (int p) {
             return es[p];
         }
 }MapManager;

 #define pii pair<int, int>

 int n, m;
 MapManager g;
 stack<int> s;
 int dfs_clock;
 int dfn[N], low[N];
 boolean instack[N];

 inline boolean init() {
     scanf("%d%d", &n, &m);
     if (!n && !m)
         return false;
     g.es.clear();
     dfs_clock = ;
     pfill(dfn, dfn + n + , );
     pfill(g.h, g.h + n + , -);
     for (int i = , u, v; i <= m; i++) {
         scanf("%d%d", &u, &v);
         g.addEdge(u, v);
     }
     return true;
 }

 int cnt_scc = ;
 void tarjan(int p) {
     dfn[p] = low[p] = ++dfs_clock;
     instack[p] = true;
     s.push(p);
     for (int i = g.h[p], e; ~i; i = g[i].nx) {
         e = g[i].ed;
         if (!dfn[e]) {
             tarjan(e);
             low[p] = min(low[e], low[p]);
         } else if (instack[e])
             low[p] = min(dfn[e], low[p]);
     }

     if (low[p] == dfn[p]) {
         int cur;
         do {
             cur = s.top();
             s.pop();
             instack[cur] = false;
         } while (cur != p);
         cnt_scc++;
     }
 }

 inline void solve() {
     cnt_scc = ;
     for (int i = ; i <= n; i++)
         if (!dfn[i])
             tarjan(i);
     puts((cnt_scc == ) ? ("Yes") : ("No"));
 }

 int main() {
     while (init())
         solve();
     return ;
 }

Strongly Conneceted Component